Отношение площадей треугольников, имеющих по равному углу.

Понятие площади. Равновеликие фигуры.

Если длина – это числовая характеристика линии, то площадь – это числовая характеристика замкнутой фигуры. Несмотря на то, что с понятием площади мы хорошо знакомы из повседневной жизни, строгое определение этому понятию дать непросто. Оказывается, что площадью замкнутой фигуры можно назвать любую неотрицательную величину, обладающую следующими свойствами измерения площадей фигур:

1. Равные фигуры имеют равные площади.
2. Если данную замкнутую фигуру разбить на несколько замкнутых фигур, то площадь фигуры равна сумме площадей составляющих ее фигур (фигура на рисунке 1 разбита на n фигур; в этом случае площадь фигуры , где S_i – площадь i-ой фигуры).

В принципе, можно было бы придумать множество величин, обладающих сформулированными свойствами, а значит, характеризующих площадь фигуры. Но наиболее привычной и удобной является величина, характеризующая площадь квадрата как квадрат его стороны. Назовем эту «договоренность» третьим свойством измерения площадей фигур:

1. Площадь квадрата равна квадрату его стороны (рисунок 2).

При таком определении площадь фигур измеряют в квадратных единицах (см², км², га=100м²).

Фигуры, имеющие равные площади, называются равновеликими.

Замечание: Равные фигуры имеют равные площади, то есть равные фигуры равновелики. Но равновеликие фигуры далеко не всегда равны (например, на рисунке 3 изображены квадрат и равнобедренный треугольник, составленные из равных прямоугольных треугольников (кстати, такие фигуры называют равносоставленными); понятно, что квадрат и треугольник равновелики, но не равны, поскольку не совмещаются наложением).

Далее выведем формулы для вычисления площадей всех основных видов многоугольников (в том числе всем известную формулу для нахождения площади прямоугольника), опираясь на сформулированные свойства измерения площадей фигур.

 

Площадь прямоугольника. Площадь параллелограмма.

Формула для вычисления площади прямоугольника: Площадь прямоугольника равна произведению двух его смежных сторон (рисунок 4).

Дано:

ABCD - прямоугольник;

AD=a, AB=b.

Доказать : S_ABCD=a×b.

Доказательство:

1. Удлиним сторону AB на отрезок BP=a, а сторону AD – на отрезок DV=b. Построим параллелограмм APRV (рисунок 4). Поскольку ÐA=90°, APRV – прямоугольник. При этом AP=a+b=AV, Þ APRV – квадрат со стороной (a+b).

2. Обозначим BCÇRV=T, CDÇPR=Q. Тогда BCQP – квадрат со стороной a, CDVT – квадрат со стороной b, CQRT – прямоугольник со сторонами a и b.

3. .                                                                                                           #

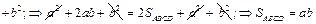Формула для вычисления площади параллелограмма: Площадь параллелограмма равна произведению его высоты на основание (рисунок 5).

Замечание: Основанием параллелограмма принято называть ту сторону, к которой проведена высота; понятно, что основанием может служить любая сторона параллелограмма.

Дано:

ABCD – п/г;

BH^AD, HÎAD.

Доказать: S_ABCD=AD×BH.

Доказательство:

1. Проведем к основанию AD высоту CF (рисунок 5).

2. BCïêHF, BHïêCF, Þ BCFH - п/г по определению. ÐH=90°, ÞBCFH – прямоугольник.

3. BCFH – п/г, Þ по свойству п/г BH=CF, Þ DBAH=DCDF по гипотенузе и катету (AB=CD по св-ву п/г, BH=CF).

4. S_ABCD=S_ABCF+S_DCDF=S_ABCF+S_DBAH=S_BCFH=BH×BC=BH×AD.                                                                             #

3. Площадь треугольника.

Формула для вычисления площади треугольника: Площадь треугольника равна половине произведения его высоты на основание (рисунок 6).

Замечание: Основанием треугольника в данном случае называют сторону, к которой проведена высота. Любая из трех сторон треугольника может служить его основанием.

Дано:

DABC;

BD^AC, DÎAC.

Доказать: .

Доказательство:

1. Достроим DABC до п/г ABKC путем проведения через вершину B прямой BKïêAC, а через вершину C – прямой CKïêAB (рисунок 6).

2. DABC=DKCB по трем сторонам (BC – общая, AB=KC и AC=KB по св-ву п/г), Þ .                                                                                                                  #

 

Следствие 1 (формула для вычисления площади прямоугольного треугольника): Поскольку в п/у D‑ке один из катетов является высотой, проведенной ко второму катету, площадь п/у D-ка равна половине произведения его катетов (на рисунке 7 ).

Следствие 2: Если рассмотреть п/у DABC с высотой AH, проведенной к гипотенузе BC, то . Таким образом, в п/у D-ке высота, проведенная к гипотенузе, равна отношению произведения его катетов к гипотенузе. Это соотношение достаточно часто используется при решении задач.

 

4. Следствия из формулы для нахождения площади треугольника: отношение площадей треугольников с равными высотами или основаниями; равновеликие треугольники в фигурах; свойство площадей треугольников, образованных диагоналями выпуклого четырехугольника.

Из формулы для вычисления площади треугольника элементарным образом вытекают два следствия:

1. Отношение площадей треугольников с равными высотами равно отношению их оснований (на рисунке 8 ).

2. Отношение площадей треугольников с равными основаниями равно отношению их высот (на рисунке 9 ).

Замечание: При решении задач очень часто встречаются треугольники с общей высотой. При этом, как правило, их основания лежат на одной прямой, а вершина, противолежащая основаниям – общая (к примеру, на рисунке 10 S₁:S₂:S₃=a:b:c). Следует научиться видеть общую высоту таких треугольников.

Также из формулы для вычисления площади треугольника вытекают полезные факты, позволяющие находить равновеликие треугольники в фигурах:

1. Медиана произвольного треугольника разбивает его на два равновеликих треугольника (на рисунке 11 у DABM и DACM высота AH – общая, а основания BM и CM равны по определению медианы; отсюда следует, что DABM и DACM равновелики).

2. Диагонали параллелограмма разбивают его на четыре равновеликих треугольника (на рисунке 12 AO – медиана треугольника ABD по свойству диагоналей п/г, Þ в силу предыдущего св-ва треугольники ABO и ADO равновелики; т.к. BO – медиана треугольника ABC, треугольники ABO и BCO равновелики; т.к. CO – медиана треугольника BCD, треугольники BCO и DCO равновелики; таким образом, S_DADO=S_DABO=S_DBCO=S_DDCO).

3. Диагонали трапеции разбивают ее на четыре треугольника; два из них, прилежащие к боковым сторонам, равновелики (рисунок 13).

Дано:

ABCD – трапеция;

BCïêAD; ACÇBD=O.

Доказать : S_DABO=S_DDCO.

Доказательство:

1. Проведем высоты BF и CH (рисунок 13). Тогда у DABD и DACD основание AD – общее, а высоты BF и CH равны; Þ S_DABD=S_DACD.

2. S_DABO=S_DABD ‑ S_DAOD=S_DACD ‑ S_DAOD=S_DDCO.                                                                                                                                           #

Если провести диагонали выпуклого четырехугольника (рисунок 14), образуется четыре треугольника, площади которых связаны очень простым для запоминания соотношением. Вывод этого соотношения опирается исключительно на формулу для вычисления площади треугольника; однако, в литературе оно встречается достаточно редко. Будучи полезным при решении задач, соотношение, которое будет сформулировано и доказано ниже, заслуживает пристального внимания:

Свойство площадей треугольников, образованных диагоналями выпуклого четырехугольника: Если диагонали выпуклого четырехугольника ABCD пересекаются в точке O, то  (рисунок 14).

Дано:

ABCD – выпуклый четырехугольник;

ACÇBD=O.

Доказать: .

Доказательство:

1. BF – общая высота DAOB и DBOC; Þ S_DAOB:S_DBOC=AO:CO.

2. DH – общая высота DAOD и DCOD; Þ S_DAOD:S_DCOD=AO:CO.

3. .                      #

Отношение площадей треугольников, имеющих по равному углу.

Теорема об отношении площадей треугольников, имеющих по равному углу: Площади треугольников, имеющих по равному углу, относятся как произведения сторон, заключающих эти углы (рисунок 15).

Дано :

DABC, DA₁B₁C₁;

ÐBAC=ÐB₁A₁C₁.

Доказать:

.

Доказательство:

1. Отложим на луче AB отрезок AB₂=A₁B₁, а на луче AC – отрезок AC₂=A₁C₁ (рисунок 15). Тогда DAB₂C₂=DA₁B₁C₁ по двум сторонам и углу между ними (AB₂=A₁B₁ и AC₂=A₁C₁ по построению, а ÐB₂AC₂=ÐB₁A₁C₁ по условию). Значит, .

2. Соединим точки C и B₂.

3. CH – общая высота DAB₂C и DABC, Þ .

4. B₂F - общая высота DAB₂C и DAB₂C₂, Þ .

5. .                                              #

 

6. Свойство биссектрисы треугольника.

С использованием теорем об отношении площадей треугольников, имеющих по равному углу, и об отношении площадей треугольников с равными высотами, просто доказывается исключительно полезный при решении задач факт, не имеющий непосредственного отношения к площадям фигур:

Свойство биссектрисы треугольника: Биссектриса треугольника делит сторону, к которой она проведена, на отрезки, пропорциональные прилежащим к ним сторонам.

Дано:

DABC;

AK – биссектриса DABC.

Доказать: .

Доказательство:

1. По теореме об отношении треугольников, имеющих по равному углу, .

2. Т.к. AH – общая высота треугольников ABK и ACK, .

3. Из пунктов 1 и 2 получаем: , Þ , Û .               #

Замечание: Поскольку в верной пропорции можно менять местами крайние члены или средние члены, свойство биссектрисы треугольника удобнее запоминать в следующем виде (рисунок 16): .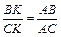

7. Площадь трапеции.

Формула для вычисления площади трапеции: Площадь трапеции равна произведению ее высоты на полусумму оснований.

Дано:

ABCD – трапеция;

BCïêAD;

BH – высота.

Доказать: .

Доказательство:

1. Проведем диагональ BD и высоту DF (рисунок 17). BHDF – прямоугольник, Þ BH = DF.

2.
.

#

Следствие: Отношение площадей трапеций с равными высотами равно отношению их средних линий (или отношению сумм оснований).

---

Дата добавления: 2020-11-29; просмотров: 362; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!