Логарифмирование обеих частей уравнения.

Методы решения логарифмических уравнений

Изученные определение логарифма, свойства логарифмов и логарифмической функции позволят нам решать логарифмические уравнения. Все логарифмические уравнения, какой бы сложности они не были, решаются по единым алгоритмам. Их немного. Если их освоить, то любое уравнение с логарифмами будет посильно каждому из вас.

Уравнение, содержащее неизвестное под знаком логарифма, называют логарифмическим.

Процесс решения любого логарифмического уравнения заключается в переходе от уравнения с логарифмами к уравнению без них.

И это решение состоит из двух равноценных частей:

1) нахождение области допустимых значений (ОДЗ),

2) решение самого уравнения.

Эти части решаются независимо друг от друга. Главное - в самом конце не забыть результаты сопоставить, лишнее выбросить.

ОДЗ - это те значения х, которые разрешены для исходного примера. А как искать ОДЗ? Внимательно осматриваем пример и ищем опасные места. Места, в которых возможны запретные действия. Таких запретных действий в математике очень мало. ( Нельзя делить на ноль, в корнях чётной степени подкоренное выражение должно быть неотрицательным, выражение стоящее под логарифмом должно быть неотрицательным и основание логарифма а >0 и а ≠1.)

Простейшие логарифмические уравнения

Уравнения вида log_а f(х) = log_а g(х)

Простейшее уравнение log_а f(х) = log_а g(х) решается методом потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их:
log_а f(х) = log_а g(х) f(х) = g(х), при f(х)>0, g(х)>0 , а > 0, а≠ 1. т.е. если равны логарифмы по одному и тому же основанию, то и равны логарифмируемые выражения. В виде равносильного перехода:

Ликвидировать логарифмы безо всяких опасений можно, если у них:

а) одинаковые числовые основания

в) логарифмы слева-справа чистые (безо всяких коэффициентов) и находятся в гордом одиночестве

-В уравнении log₃х = 2log₃(3х-1) убирать логарифмы нельзя. Двойка справа не позволяет. Коэффициент.

- В примере log₃х+log₃(х+1) = log₃(3+х) тоже нельзя потенцировать уравнение. В левой части нет одинокого логарифма. Их там два.

Короче, убирать логарифмы можно, если уравнение выглядит так и только так: log_а(.....) = log_а(.....)

В скобках, где многоточие, могут быть какие угодно выражения. Простые, суперсложные, всякие. Важно то, что после ликвидации логарифмов у нас остаётся более простое уравнение

Пример 1. Решите уравнение: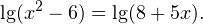

Решение: способ 1. В область допустимых значений (ОДЗ) входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:

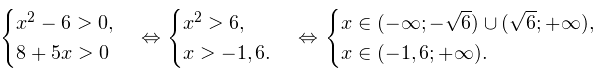
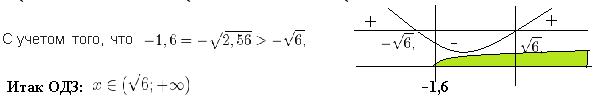
Видим логарифмы по одному и тому же основанию равны, значит, равны и логарифмируемые выражения.

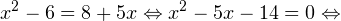
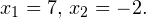
В область допустимых значений входит только первый корень.

Ответ: 7. ОДЗ можно было не решать, а просто записать. В конце каждый корень подставить в ОДЗ. Если с каждым неравенством ОДЗ получится верное числовое неравенство, то он идет в

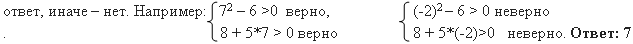Решение: способ 2. Если это уравнение решим путем равносильных переходов, то ОДЗ нашли бы без всяких квадратных неравенств и пересечений. Итак

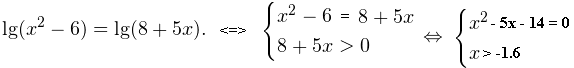Уравнение х² - 5х – 14 = 0 имеет корни х₁ = 7, х₂ = -2. В область допустимых значений входит только первый корень. Ответ: x = 7.

Пример 2. Решите уравнение lg(x²-4x-5) = lg (5-x).

Решение. Решим методом равносильных переходов. Тогда уравнение равносильно системе

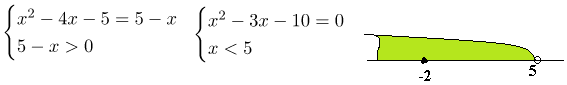
Корни уравнения -2 и 5. Только -2 ϵ ОДЗ. Ответ: -2

Итак уравнения такого вида решили 2-мя способами: 1)отдельно найдя ОДЗ и отдельно решив само уравнение; 2)используя равносильные переходы. Какой способ вам по душе?

Уравнения вида log_a f (x) = b

Уравнение log_a f (x) = b - простейшее логарифмическое уравнение, где а и b - числа; а >0, a≠1. Переменная х присутствует только внутри аргумента.

Способы решения :

1) Применение определения логарифма

2)Представление числа в виде логарифма: b = log_a a^b

Решение уравнений применением определения логарифма

Решение уравнения
основано на применении определения логарифма и в решении равносильного уравнения

Для уравнений log_a f (x) = b записывать область определения не нужно (f (x) >0), потому что она будет выполняться автоматически. Так как в какую бы степень мы бы не возводили положительное число а, на выходе мы все равно получим положительное число, т.е. если а > 0, то a^b > 0 всегда => f (x) = a^b > 0.

Пример 1. Решите уравнение log₅(x – 2) = 1

Решение: Переменная х встречается лишь в одном log и стоит в его аргументе, значит находить ОДЗ не надо. log₅(x – 2) = 1; x – 2 = 5¹; x – 2 = 5; x = 7. Ответ: 7.

Пример 2. Решите уравнение: log_0,5 (3x − 1)=-3.

Решение: Это простейшее логарифмическое уравнение, поэтому нет необходимости найти ОДЗ, потому что 3х – 1>0 будет выполняться автоматически. Слева у нас стоит выражение с логарифмом, а справа – число. Что делать? Нужно сделать так, чтобы справа тоже было выражение с логарифмом по основанию 0,5 а затем просто «сбросить» логарифмы. Так как −3=−3*1=-3*log_0,5 0,5=log_0,5 0,5⁻³ тогда уравнение примет вид: log_0,5 (3x − −1) = log_0,5 0,5⁻³. Потенцируем уравнение.

Все десятичные дроби переводите в обыкновенные, когда вы решаете логарифмическое уравнение.

Заметим что 0,5^-3 = (1/2)⁻³ = (2^-1)^-3 = 2³ = 8 и получим

3x − 1 = 8

3x = 9

x = 3

Ответ: 3.

Пример 3. Решите уравнение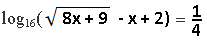

Решение: Это простое логарифмическое уравнение, поэтому можно не найти ОДЗ. Первый шаг- дробь справа представим в виде логарифма. Получим:

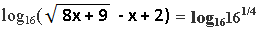Учитывая, что 16^1/4 = (2⁴)^1/4 = 2

избавляемся от знака логарифма и получаем обычное иррациональное уравнение: 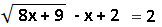где надо будет учесть ОДЗ.

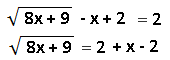
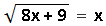, решим равносильным переходом к системе:

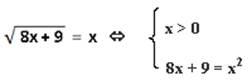
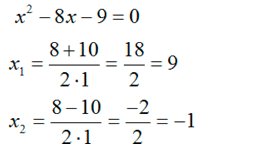
Из полученных корней нас устраивает только первый, так как второй корень меньше нуля. Единственным ответом будет число 9. Ответ: 9.

Уравнения, решаемые применением свойств логарифмов

Схема решения не простых логарифмических уравнений

1. Привести уравнение с помощью свойств логарифмов к виду:

log _а f(x) = b или log_а f(x) = log_а g(x).

2. Решить равносильное уравнение

f(x) = a ^b или f(x) = g(x) по их алгоритму.

Пример 1. Решите уравнение .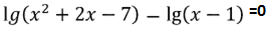

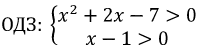
Если lg(x – 1) переведем в правую часть уравнения, то получим уравнение 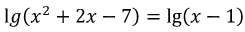вида log_а f(х) = log_а g(х).

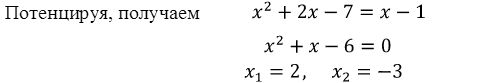
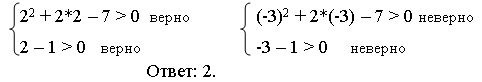
Если неравенства неудобные, ОДЗ можно не решать. Достаточно подставить результаты уравнения в записанные условия ОДЗ и проверить, какие решения проходят. Их и взять за ответы

Пример 2. Решите уравнение lg(3x-11)+lg(x-27)=3.

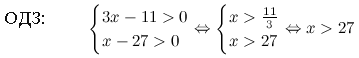
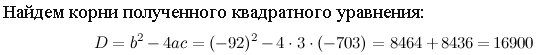
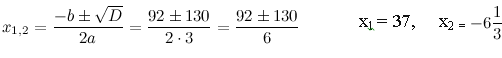
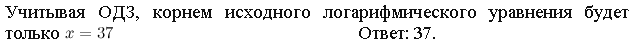
Если в уравнении содержатся логарифмы с разными основаниями, то, прежде всего, следует свести все логарифмы к одному основанию, используя формулы перехода 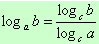, 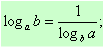и

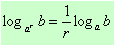
Уравнения, решаемые введением новой переменной

Если, в уравнение неоднократно, встречается некоторое определенное выражение, то оно решается введением новой переменной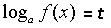

Пример 1. Решите уравнение .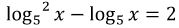

ОДЗ: x > 0. Введем новую переменную тогда получим квадратное уравнение:

y² – y = 2,

y² – y – 2 = 0,

y₁ = 2 или y₂ = -1

или

x = 25 или x = 5^-1

x =

Ответ: 25;

Пример 2. Решите уравнение .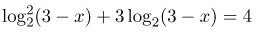

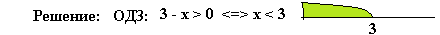
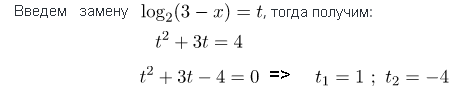
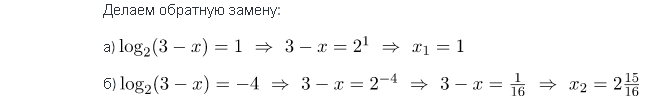Оба корня удовлетворяют ОДЗ нашего уравнения.

Пример 3. Решите уравнение 4 log₂₅5x + log²₅x – 5 = 0; ОДЗ: x > 0.

Тут 2 основания, выполним переход к основанию 5, используя формулу

2 log₅5x + log²₅x – 5 = 0; Применим формулу log_axy = log_ax + log_ay

2(log₅5 + log₅x) + log²₅x – 5 = 0.

2(1 + log₅x) + log²₅x – 5 = 0.

Пусть log₅x = t, тогда 2(1 + t) + t² – 5 = 0;

t² + 2t – 3 = 0;

(t + 3)(t – 1) = 0;

t = – 3 или t = 1; Обратно переходим на обозначение log₅x = t:

log₅x = – 3, log₅x = 1;

x = 5^-3, x = 5;

x = 1/125. Оба корня удовлетворяют ОДЗ. Ответ: 5 и 1/125.

Уравнения, содержащие неизвестное и в основании и в аргументе.

Уравнения вида log _f(x)g(x) = b

Уравнение log _f(x)g(x) = b похоже простейшему уравнению log_a f (x) = b Сходство: в обеих уравнениях в левой части log, в правой число b. Отличие в том, что в первой переменная х присутствует не только внутри аргумента, но и в основании логарифма.

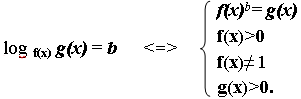
Но мы должны учесть определенные требования. 1) аргумент каждого из логарифмов должен быть больше 0: 2) основание должно быть не только больше 0, но и отлично от 1

Способы решения :

1) Применение определения логарифма

2)Представление числа в виде логарифма

Пример 1. Решить уравнение: log _{x – 1}(x² – 5x + 10) = 2.

Решение: ОДЗ: x² – 5x + 10 > 0, x – 1 > 0, x – 1 ≠ 1.

По определению логарифма х² – 5х + 10 = (х - 1)² х² – 5х + 10 =:х² – 2х + 1, -3х = -9 х = 3

Проверим принадлежность х = 3 ОДЗ: 3² – 5*3 + 10 > 0 верно, 3 – 1 > 0 верно 3 – 1 ≠ 1 верно

Ответ: 3.

Пример 2. Решите уравнение log _х+1(2x²+1)=2 Решение: Решим методом равносильных переходов. Заменяем 2 на 2=2*1=2* log _{х + 1}(х+1)= log _{х + 1}(х+1)² тогда получим: log _х+1(2x²+1)= log _х+1(x+1)²

Наше уравнение содержит неизвестное и в основании и в аргументе. Поэтому 1) аргумент каждого из логарифмов должен быть больше 0. 2) основание должно быть не только больше 0, но и ≠ 1. В итоге получим систему:

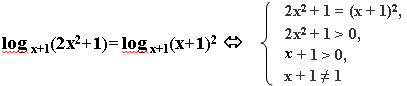
Решим уравнение 2х²+1=(х+1)², 2х² + 1 = х² + 2х + 1 х² - 2x = 0 ó x(x - 2) = 0 ó x=2 или x=0. х=0 не соответствует системе. Ответ: 2.

Способ 2. ОДЗ: 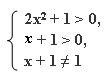по определению логарифма получим: 2х²+1 = (х+1)², 2х²+1 = х² +2х + 1, х² – 2х = 0 ó x(x – 2) = 0 ó x = 0, x = 2. Корень х = 0 не удовлетворяет третьему неравенству ОДЗ.

Ответ: 2

Уравнения вида log _h(x)f(x) = log _h(x)g(x)

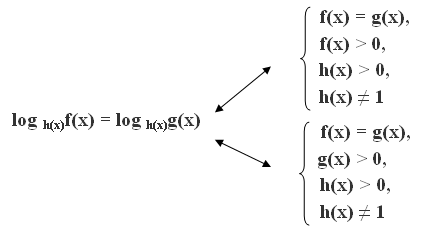
Пример 1. Решите уравнение log _3x(x² – 5x) = log _3x(4x – 8)

Логарифмирование обеих частей уравнения.

Дата добавления: 2020-11-29; просмотров: 3122; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!