Дифференцирование параметрически заданных функций
Пусть зависимость между аргументом x и функцией y задана параметрически в виде двух уравнений
(1.11)
где t – вспомогательная переменная, называемая параметром.
Найдем производную 
, считая, что функции (1.11) имеют производные и что функция 
имеет обратную 
. По правилу дифференцирования обратной функции
. (1.12)
Функцию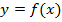 
, определяемую параметрическими уравнениями (1.11), можно рассматривать как сложную функцию 
. По правилу дифференцирования сложной функции имеем: 
.
С учетом равенства (1.12) получаем
.
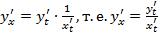Полученная формула позволяет находить производную от функции, заданной параметрически, не находя непосредственной зависимости y от x.
Пример. Пусть 
Найти .
Решение. Имеем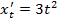 
, 
. Следовательно, 
.
В этом можно убедиться, найдя непосредственно зависимость y от x. Действительно, 
. Тогда 
. Отсюда 
.
Логарифмическое дифференцирование
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продифференцировать. Такую операцию называют логарифмическим дифференцированием.
Связь между непрерывностью и дифференцируемостью. Дифференциал функции.
Теорема. Если функция у(x) = f(x) дифференцируема в своей области определения, то она непрерывна. Обратное не верно: из непрерывности функции дифференцируемость не следует.
|
|
|
Доказательство. Дифференцируемость означает наличие производной
(1.13)
Используем теорему о разности между функцией и ее пределом:
если 
, то f (x) = A + a (х), (1.14)
где a (х) величина бесконечно малая.
Сравнивая выражения (1.13) и (1.14) получим, что в нашем случае
A 
y’(x), f(x) 
, 
т.е. = y ’(x) +a (Δх). (1.15)
Умножим (1.15) на Δх
. (1.16)
Из (1.16) следует, что если 
, то и 
, что является доказательством непрерывности функции.
Приведем пример показывающий, что непрерывная функция может быть не дифференцируемой. Возьмем функцию
Эта функция непрерывна на всей области определения, так как в точке х0 = 0 выполняется соотношение
= 
= f(x0).
Действительно, 
и 
= f(x0).
Следовательно, в точке 0 функция непрерывна. Но производной в этой точке нет, так как слева при x < 0, y’(x) = -1, а справа при x > 0 y’(x) = 1.
Вернемся к формуле (1.16). Дифференциалом df(x) функции f(x) в точке х называется линейная по Dx часть приращения функции (равная произведению производной функции на приращение аргумента)
|
|
|
df(x) = 
. (1.17)
По определению для независимой переменной Δх = dx. Поэтому дифференциал функции f(x) записывают чаще так
(1.18)
Формула (1.18) сохраняется и в том случае, когда х зависимая переменная (формула (1.17) для зависимой переменной неверна).
Иными словами, дифференциал функции равен произведению функции на дифференциал независимой переменной.
Геометрический смысл дифференциала (рис.1.2).
Производная f ¢(x) численно равна тангенсу угла наклона касательной к графику функции f(x). Дифференциал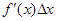 
равен приращению ординаты касательной к графику функции в точке N (когда x получит приращение Δx). Замена истинного приращения функции NB Df(x) = f(x + Dx) - f(x) на дифференциал СВ 
равносильна замене части графика функции на соответствующую часть касательной к этому графику (см. также рис.1.1).
Производная f¢(x) является функцией того же аргумента х, что и исходная функция. Поэтому ее можно опять дифференцировать, т.е. вычислять предел отношения приращения производной к приращению аргумента
Рис. 1.2 Геометрический смысл дифференциала
|
|
|
= 
.
Если этот предел существует и конечен, то он называется второй производной от функции f(x) в точке х. Принятое обозначение:
Подобным образом вводят производные n-го порядка f(n)(x) = (f(n-1)(x))¢. В механике вторая производная от пути по времени есть ускорение 
Пример. Производные от степенной функции y = хn.
y¢ = n xn-1,
y¢¢ = n (n-1) xn-2,
y¢¢¢ = n (n-1) (n-2) xn-3,
...,
y(k) = n (n-1) (n-2)...(n-k+1) x(n-k) при (к £ n).
Дифференциалом второго порядка называется дифференциал от первого дифференциала
d(df(x)) = (df(x))¢Dx = (f ¢(x)Dx)¢Dx = f ¢¢(x) (Dx)2.
Дата добавления: 2020-11-29; просмотров: 141; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!