Произвести полное исследование функции:
Тульский филиал
федерального государственного бюджетного образовательного учреждения
высшего образования
«Российский экономический университет имени Г.В. Плеханова»
(Тульский филиал РЭУ им. Г.В. Плеханова)
Кафедра финансов и информационных технологий управления
Контрольная работа
по дисциплине
«Математический анализ»
на тему:
«Исследование функции»
Выполнил:
Студент 1 курса
Очной формы обучения
Направления «Экономика»
Годованный Егор Викторович
Проверил профессор технических наук:
Юдин Сергей Владимирович
Тула 2020
Группа № 3 Вариант 7
Найти экстремумы функции:
#1. 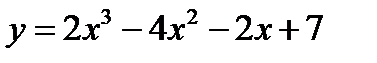
#2. 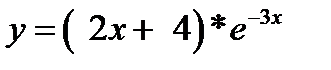
#3. 
Найти минимальное и максимальное значение функции:
#4.  на отрезке [2, 12]
на отрезке [2, 12]
#5.  на отрезке [4, 13]
на отрезке [4, 13]
#6.  на отрезке [2, 13]
на отрезке [2, 13]
Найти асимптоты функции:
#7. 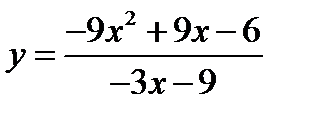
#8. 
#9. 
Произвести полное исследование функции:
#10. 
#11. 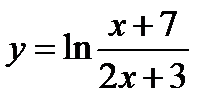
#12. 
#13. 
#14 
#15. 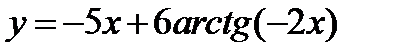
Вычислить при помощи 1-го дифференциала:
#16.  в точке x=-0.001.
в точке x=-0.001.
#17. 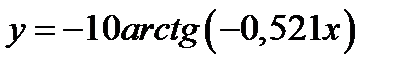 в точке x=-0.004.
в точке x=-0.004.
#18. 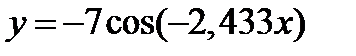 в точке x=-0.001.
в точке x=-0.001.
#19. 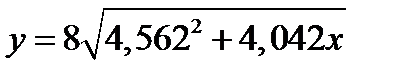 в точке x= 0.006.
в точке x= 0.006.
#20. 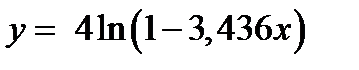 в точке x=-0.008.
в точке x=-0.008.
#21. 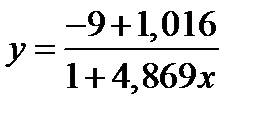 в точке x= 0.009.
в точке x= 0.009.
Ответы:
№1. 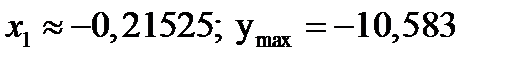 .
. 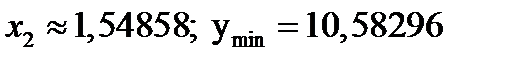 .
.
№2.  .
.
№3.  .
.
№4.  .
.  .
.
№5.  .
.
№6.  .
.  .
.
№7.  - наклонная асимптота;
- наклонная асимптота; 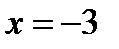 - вертикальная асимптота.
- вертикальная асимптота.
№8.  - наклонная асимптота;
- наклонная асимптота; 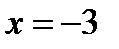 - вертикальные асимптоты.
- вертикальные асимптоты.
№9. наклонные асимптоты:  .
.
№10.
№11.
№12.
№13.
№14.
№15.
№16. -5,9844
№17. -0,02084
№18. -7
№19. 36,51726
№20. 0,10995
№21. -7,634113
Найти экстремумы функций:
№1. 
Решение:
1) Найдем стационарные точки, которые определяются тем, что в этих точках производная обращается в нуль или не существует.
|
|
|

Решив данное уравнений, получим: 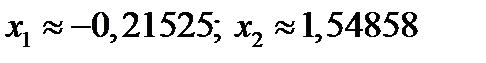
2) Проверим эти точки на экстремум. Для этого необходимо найти вторую производную. Если в стационарной точке y"¹ 0, то эта точка является точкой экстремума, причем, если y"> 0 – имеется минимум; если y"< 0 – максимум:

Ответ: 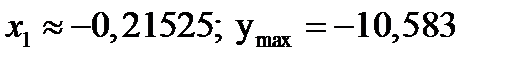
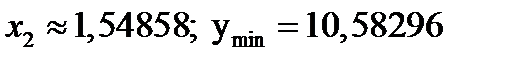
№2. 
Решение:
1) Найдем стационарные точки, которые определяются тем, что в этих точках производная обращается в нуль или не существует.
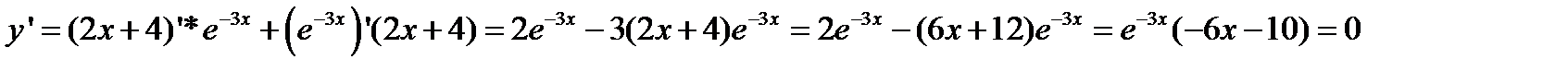
Отсюда 
2) Исследуем эту точку на экстремумы:

Ответ: 
№3. 
Решение:
1) Найдем стационарные точки, которые определяются тем, что в этих точках производная обращается в нуль или не существует.

Отсюда 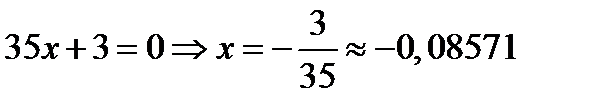
2) Исследуем точку на экстремум:
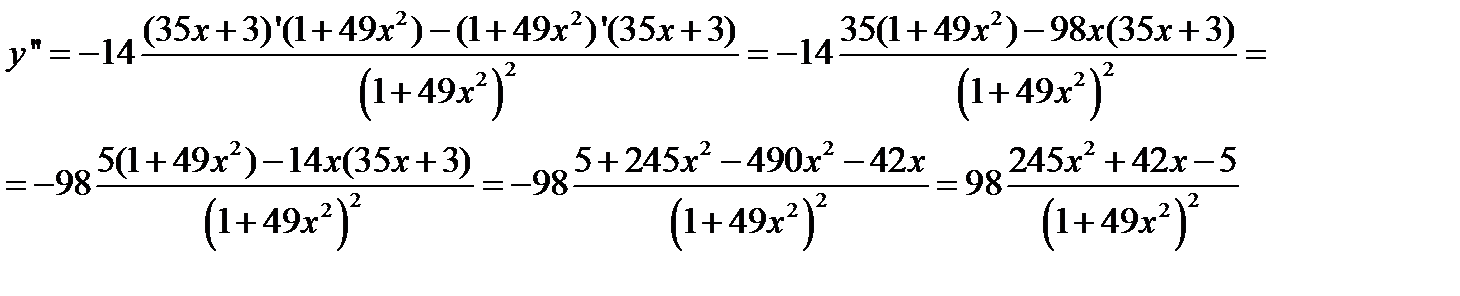

Ответ: 
Найти минимальное и максимальное значение функций:
№4.  на отрезке [2, 12]
на отрезке [2, 12]
Решение:
Минимальное и максимальное значения функции могут достигаться или в стационарных точках внутри исследуемого отрезка, или в особых точках внутри отрезка (точки разрыва, точки разрыва первой или второй производной и т.д.), или на границах отрезка.
1) Найдем стационарные точки. Производная равна 
Отсюда имеем: 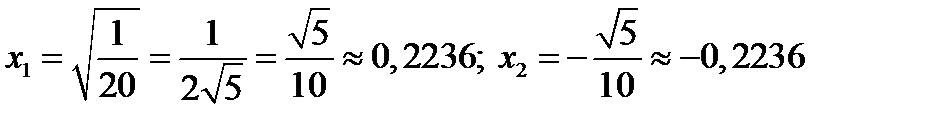
Эти точки не принадлежат исследуемому отрезку.
|
|
|
2) Особых точек нет.
3) На левой границе  функция принимает значение
функция принимает значение  ; на правой границе
; на правой границе 
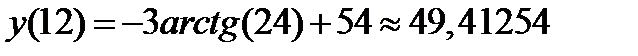
Ответ: 
№5.  на отрезке [4, 13]
на отрезке [4, 13]
Решение:
1) Найдем стационарные точки: 
Эти точки не принадлежат исследуемому отрезку.
2) Особых точек внутри отрезка нет.
3)  ;
; 
Ответ: 
№6.  на отрезке [2, 13]
на отрезке [2, 13]
1) Найдём стационарные точки: 
Получаем: 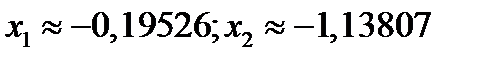 - эти точки не принадлежат исследуемому отрезку.
- эти точки не принадлежат исследуемому отрезку.
2) Особых точек нет.
3)  ;
; 
Ответ: 
Найти асимптоты функции:
№7. 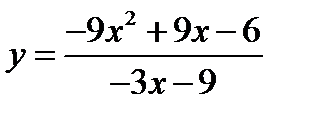
Решение:
Уравнение наклонной асимптоты y = ax + b, если она имеется, определяется следующим образом:

Вертикальная асимптота определяется точкой бесконечного разрыва функции.
1) Найдём наклонную асимптоту функции.
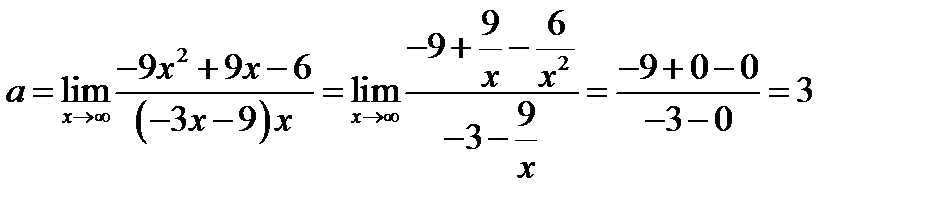
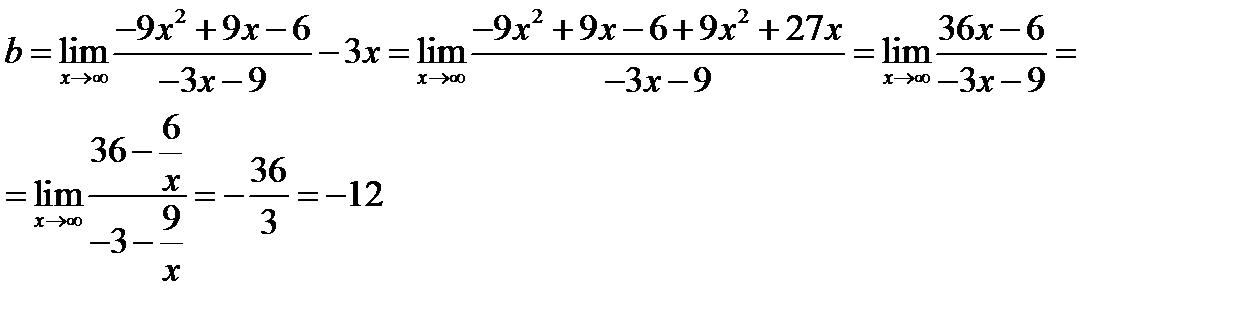
Таким образом, уравнение наклонной асимптоты имеет вид: 
2) Вертикальная асимптота задается точкой, в которой обнуляется знаменатель, т.е.
 Отсюда:
Отсюда: 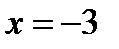
Ответ:  -наклонная асимптота;
-наклонная асимптота; 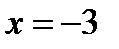 - вертикальная асимптота
- вертикальная асимптота
№8. 
Решение:
Уравнение наклонной асимптоты y = ax + b, если она имеется, определяется следующим образом:

Вертикальная асимптота определяется точкой бесконечного разрыва функции.
1) Найдём наклонную асимптоту функции.


Таким образом, уравнение наклонной асимптоты имеет вид: 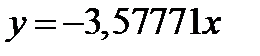
2) Вертикальная асимптота задается точкой, в которой обнуляется знаменатель, т.е.
|
|
|
 Отсюда:
Отсюда: 
Ответ:  - наклонная асимптота;
- наклонная асимптота; 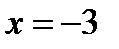 - вертикальные асимптоты.
- вертикальные асимптоты.
№9. 
Решение:
Вертикальных асимптот нет.
Наклонные асимптоты:
1) Рассмотрим случай, когда 
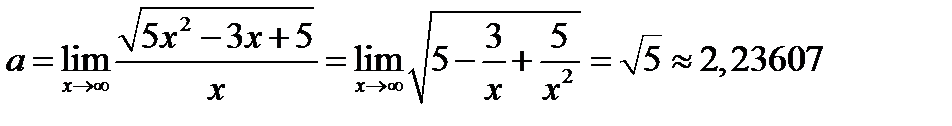

2) Рассмотри случай, когда 
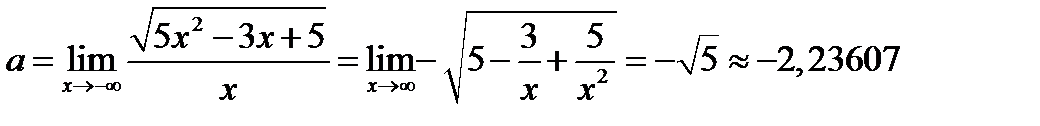

Таким образом, уравнения наклонных асимптот имеют вид: 
Ответ: наклонные асимптоты: 
Произвести полное исследование функции:
№10. 
Решение:
Схема исследования функции:
1) Область определения.
2) Симметрия.
3) Точки пересечения с осями координат.
4) Точки разрыва, вертикальные асимптоты.
5) Наклонные асимптоты.
6) Точки экстремума. Интервалы монотонности.
7) Точки перегиба. Интервалы выпуклости и вогнутости.
8) Построение графика.
1) О.О.Ф. 
2) Т.к., 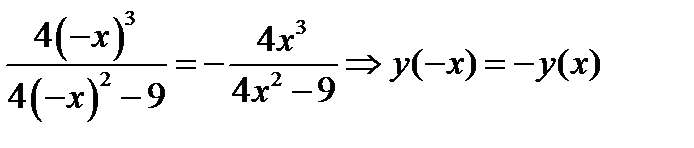 , то функция антисимметричная (нечетная).
, то функция антисимметричная (нечетная).
3) Точки пересечения с осями координат:
С осью абсцисс: 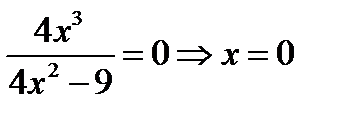
С осью ординат: 
Следовательно точка пересечения с осями координат M1(0;0)
4)  - точки разрыва и вертикальные асимптоты.
- точки разрыва и вертикальные асимптоты.
Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках:
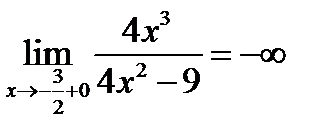 ;
; 
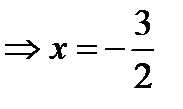 - точка разрыва второго рода.
- точка разрыва второго рода.
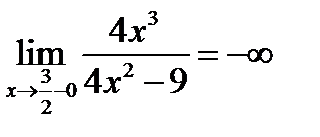 ;
; 
 - точка разрыва второго рода.
- точка разрыва второго рода.
5) Наклонные асимптоты:

Уравнение наклонной асимптоты: 
При x ®+¥ функция будет находиться над асимптотой, а при x ®-¥ функция будет находиться под асимптотой.
|
|
|
6) Точки экстремума:

Она обращается в ноль при 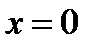 и
и 
1. На интервале (-∞; -2,59808] y’(x) >0 функция возрастает
2. На интервале [-2,59808; -1,5) y’(x) <0 функция убывает
3. На интервале (-1,5; 0] y’(x) <0 функция убывает
4. На интервале [0; 1,5) y’(x) <0 функция убывает
5. На интервале (1,5; 2,59808] y’(x) <0 функция убывает
6. На интервале [2,59808; +∞] y’(x) >0 функция возрастает
Таким образом функция имеет два экстремума: точка x=-2,59808 – точка максимума, а точка x=2,59808 – точка минимума.
7) Вторая производная равна:
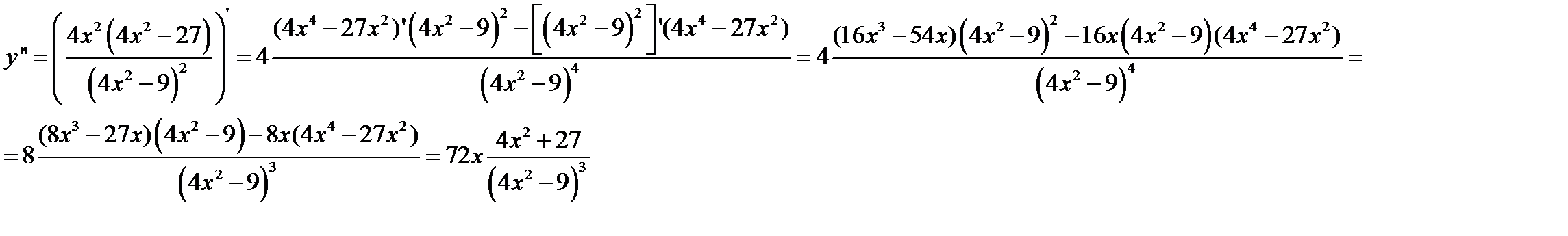
Она обращается в ноль при x=0 – это точка перегиба.
1. На интервале (-∞; -1,5) y’’(x) <0 функция выпукла
2. На интервале (-1,5; 0] y’’(x) >0 функция вогнута
3. На интервале [0; 1,5) y’’(x) <0 функция выпукла
4. На интервале (1,5; +∞) y’’(x) >0 функция вогнута
8) Теперь можно построить график функции:

№11. 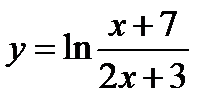
1) О.О.Ф.: 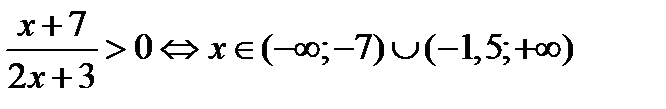
В интервале 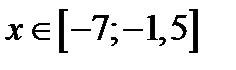 функция не определена.
функция не определена.
2) Симметрия четности отсутствует.
3) Точки пересечения с осями координат:
При  график пересекает ось Oy в точке
график пересекает ось Oy в точке 
y=0 при 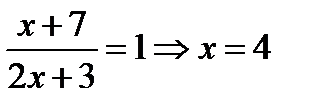 - точка, в которой графики пересекает ось Ox.
- точка, в которой графики пересекает ось Ox.
3) Точки разрыва: 
При 
При 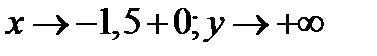
5) Наклонные асимптоты:
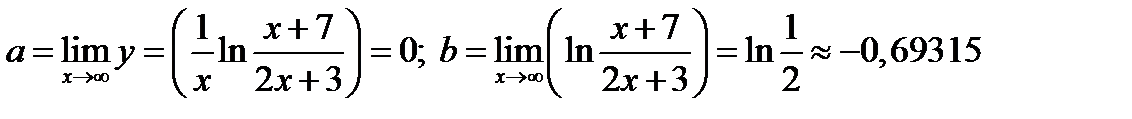
Уравнение наклонной асимптоты: 
При x ®+¥ функция будет находиться над асимптотой, а при x ®-¥ функция будет находиться под асимптотой.
6) Точки экстремума:
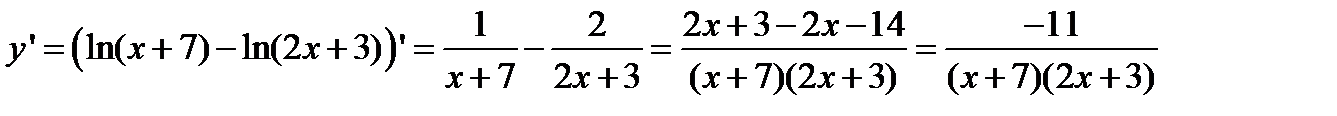
Точек с нулевой производной нет. Функция монотонна.
При x < -7 производная отрицательная; при x > -1,5 производная отрицательная. Таким образом, функция монотонно убывает на обоих интервалах определения.
7) Вторая производная равна:
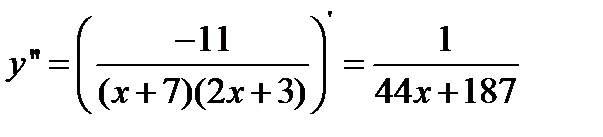
При y’’=0 не существует ни одного x, следовательно точек перегиба для этой функции не существует. При x < -7 график функции выпуклый, а при x > -1,5 график функции вогнутый.
8) Теперь можно построить график функции:
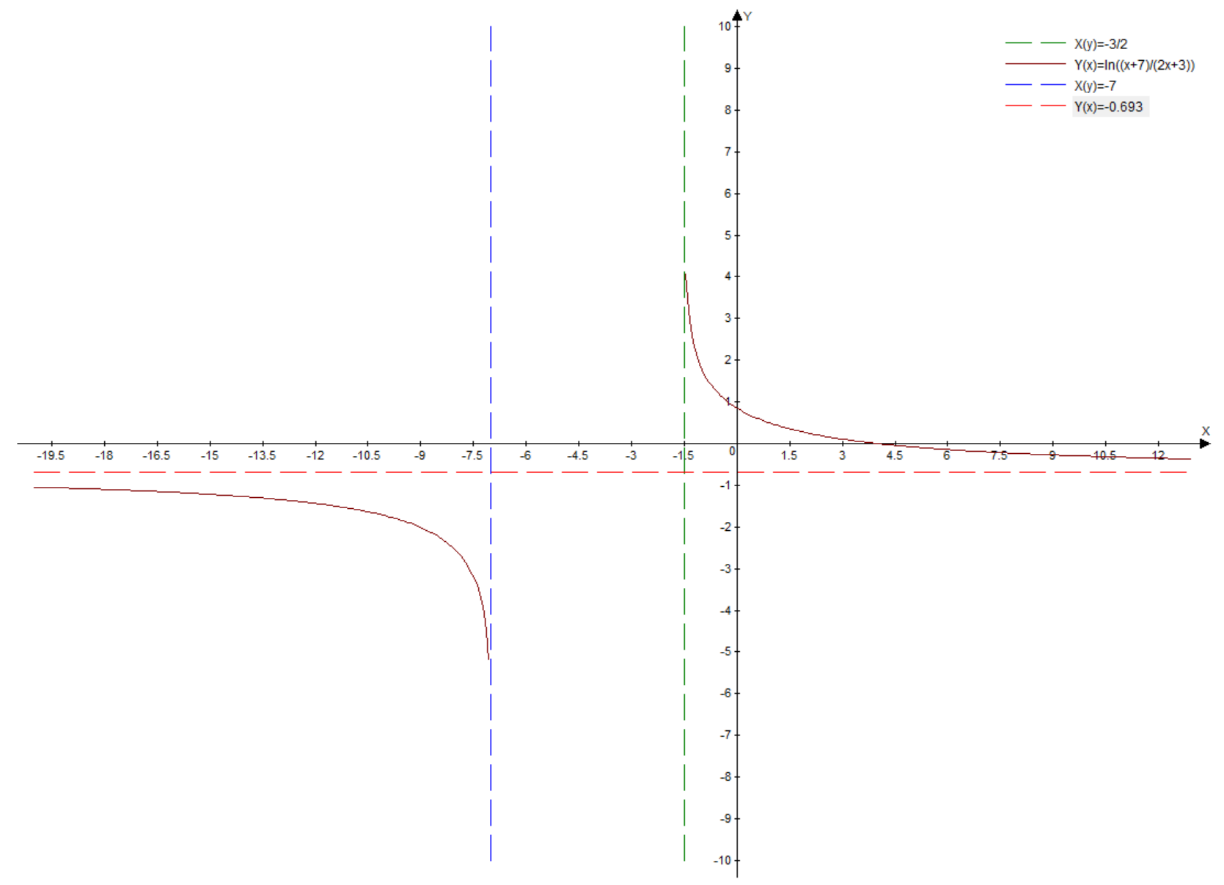
№12. 
1) Область определения функции: x - любое действительное число.
2) Симметрия отсутствует.
3) Точки пересечения с осями координат.
При x =0:  ;
;
при y =0: x = -0,66667.
4) Точек разрыва и вертикальных асимптот нет.
5) Наклонные асимптоты. Здесь придется рассмотреть два отдельных случая:
2. x ®¥ : 
Таким образом, при x ® ¥ наклонная асимптота имеет вид: y=0
2. x ®-¥ :  . Таким образом, при x ®-¥ асимптоты нет.
. Таким образом, при x ®-¥ асимптоты нет.
6) Точки экстремума. Интервалы монотонности.

Производная обращается в ноль при x = -0,35. При x> -0,35 производная положительна, т.е. функция возрастает; при x < -0,35 производная отрицательна, т.е. функция убывает. x = -0,35 - точка максимума.
7) Точки перегиба. Выпуклость и вогнутость.

Вторая производная обращается в ноль при x = -0,1. При x < -0,1 вторая производная отрицательная, т.е. график функции выпуклый; при x > -0,1 она положительная, т.е. график функции вогнутый.
8) Теперь можно строить график функции:

№13. 
1) ООФ: xÎR.
2) Симметрия отсутствует.
3) Точки пересечения с осями координат:
При x =0: y =-2,51984; y=0 при x1 =-4; x2 =-2; x3=2
4) Точек разрыва и вертикальных асимптот нет.
5) Наклонные асимптоты:
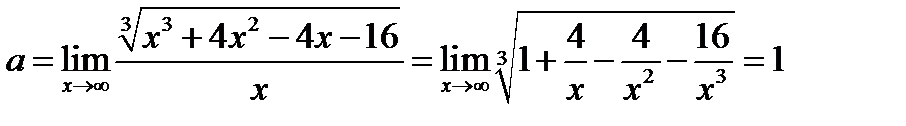
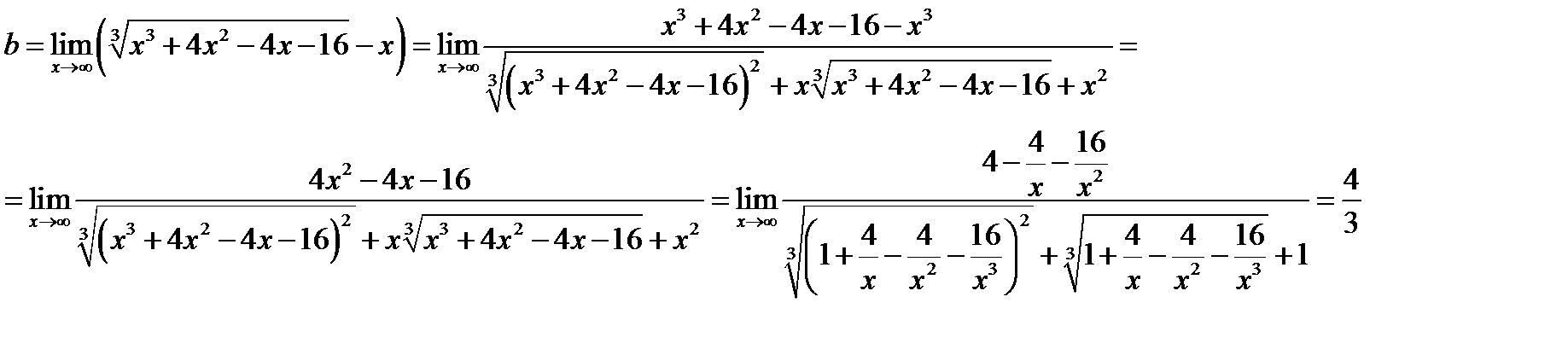
Таким образом, наклонная асимптота имеет вид: 
6) Точки экстремума. Интервалы монотонности.
Производная равна 
Отсюда получаем, что y’=0 при x4=-3,09717 и x5=0,4305.
Помимо этого, следует отметить, что при x1=-4, x2=-2, x3=2 первая производная терпит разрыв, и ее значение в этих точках стремится к бесконечности. Таким образом, график функции в этих точках вертикален.
При x < -3,09717 y'>0 - функция возрастает.
При -3,09717 < x < 0,4305 y’<0 – функция возрастает.
При x > 0,4305 y’>0 – функция возрастает.
Таким образом, x4=-3,097171 - точка максимума; x5=0,4305 - точка минимума.
7) Точки перегиба. Выпуклость и вогнутость.
Вторая производная равна

В данном случае 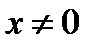 .
.
При x<-4 y’’(x) <0 функция выпуклая
При -4<x<-2 y’’(x) >0 функция вогнутая
При -2<x<2 y’’(x) <0 функция выпуклая
При x>2 y’’(x) >0 функция вогнутаz
8) Теперь можно строить график функции.
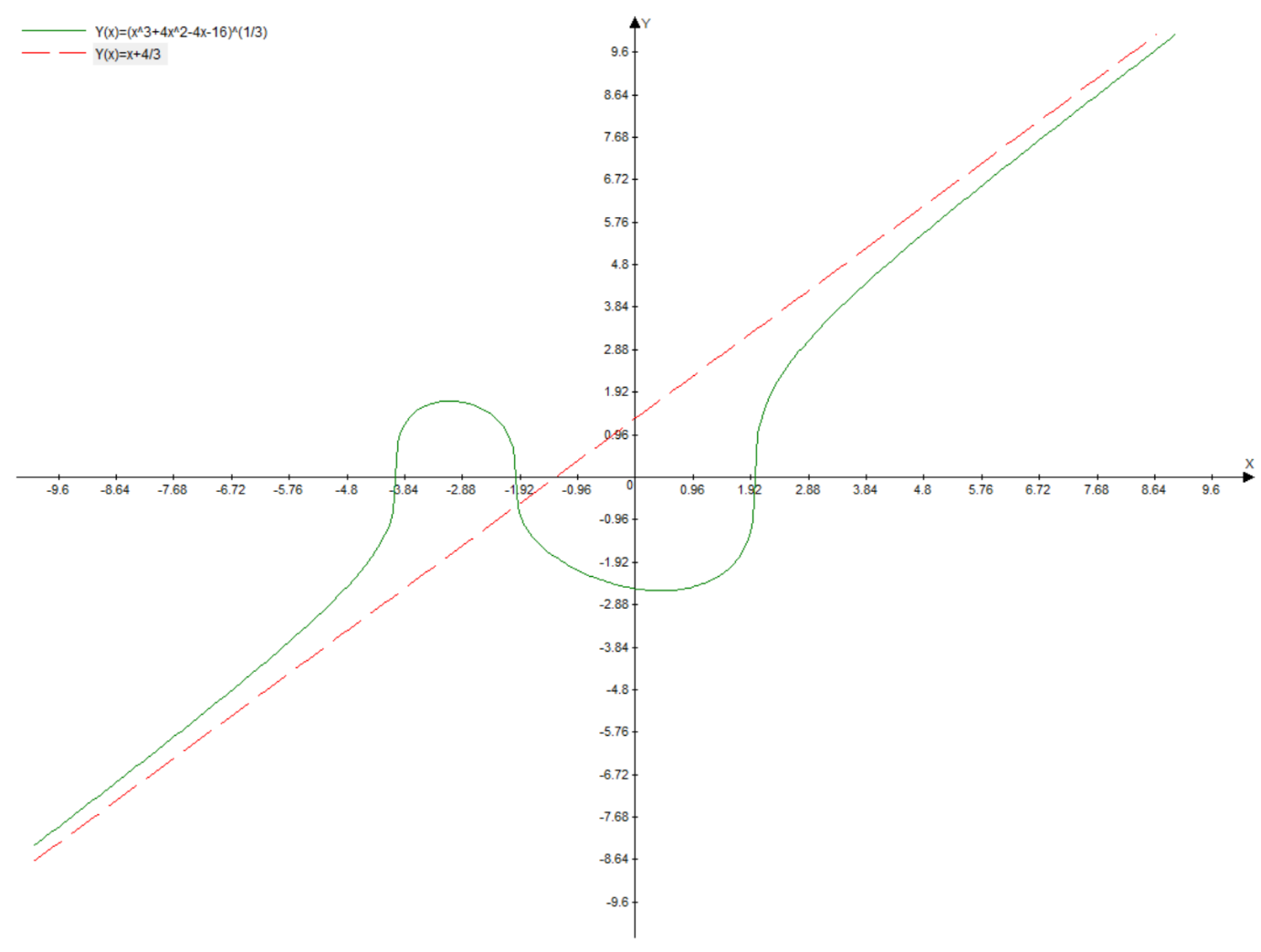
№14. 
1) Область определения функции: 
2) Симметрия отсутствует.
3) Точки пересечения с осями координат: отсутствуют.
4) Точки разрыва: 
При  ; при
; при 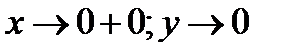
Прямая x =0 - вертикальная асимптота.
5) Наклонные асимптоты
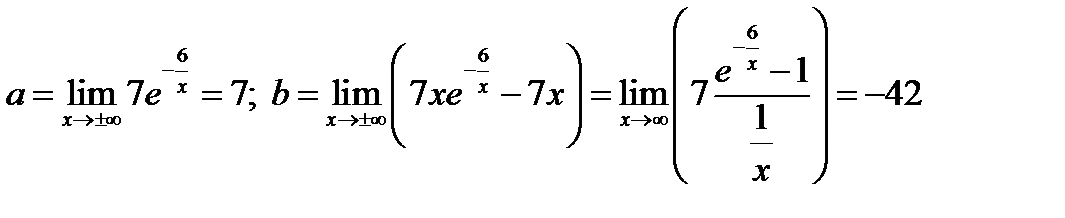
Таким образом, прямая y = 7x - 42 является наклонной асимптотой функции.
При x ®+¥ график функции находится над асимптотой, при x ®-¥ график функции находится под асимптотой.
6) Точки экстремума. Интервалы монотонности.
Производная равна 
 при x=-6
при x=-6
При x < -6 y' >0 - функция возрастает;
При - 6<x<0 y'<0 – функция убывает;
При 0<x y' >0 - функция возрастает.
Таким образом, точка x = -6 - точка максимума.
7) Точки перегиба. Выпуклость и вогнутость.
Вторая производная равна 
 точек перегиба нет.
точек перегиба нет.
8) Теперь можно приступать к построению графика функции.
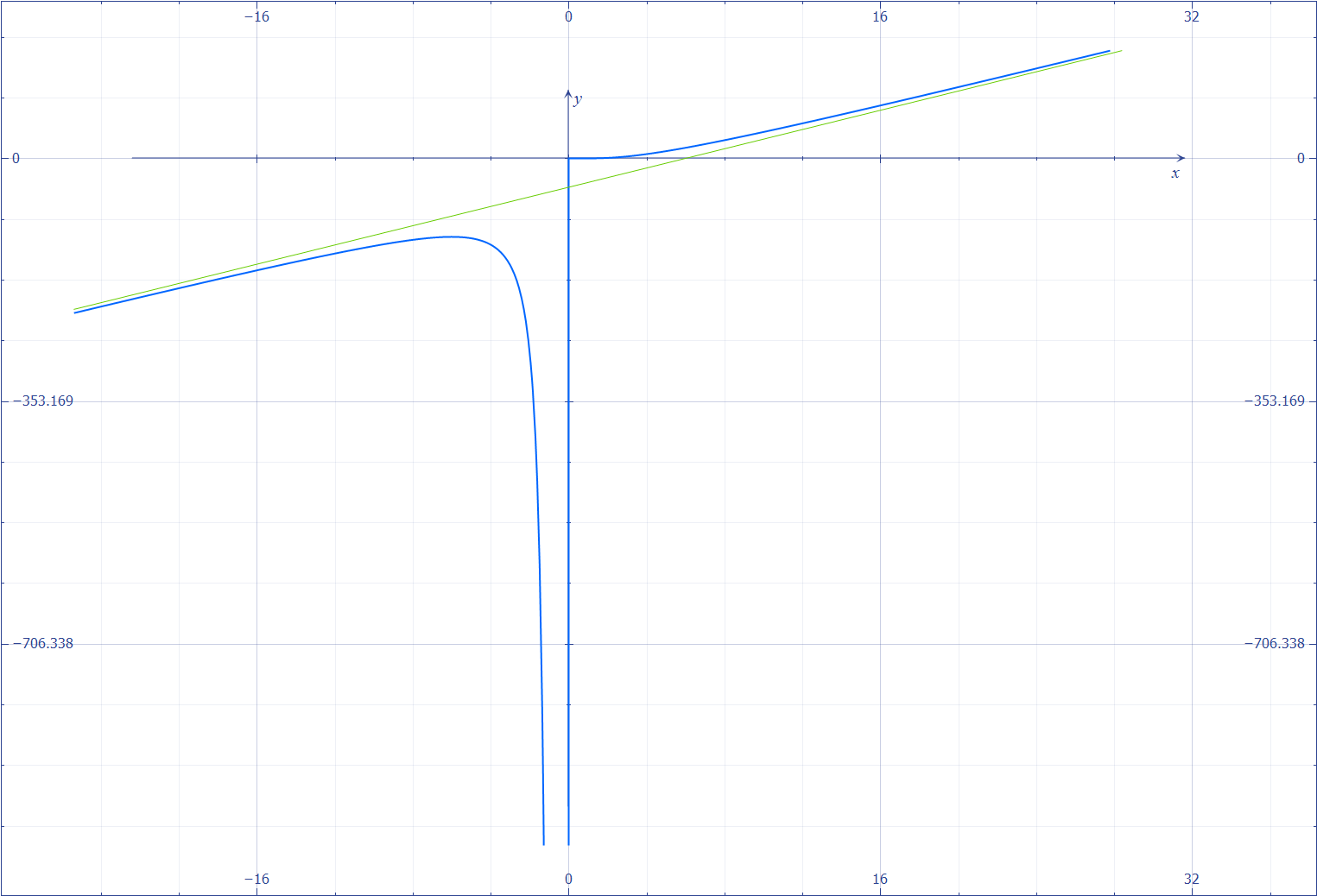
Синий график: 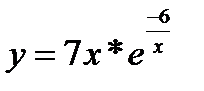 ; зелёный график: y = 7x - 42
; зелёный график: y = 7x - 42
№15. 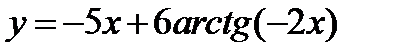
Решение:
1) Область определения: x - любое действительное число.
2) Симметрия: 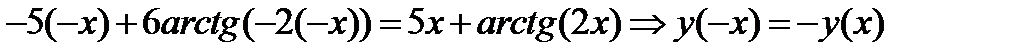
Следовательно функция нечетная.
3) Точки пересечения с осями координат.
При x =0 y =0.
4) Точки разрыва, вертикальные асимптоты: отсутствуют.
5) Наклонные асимптоты.
1. При  :
:
 ;
; 
Таким образом, при x ®+¥ асимптота имеет вид y=-5x-9,42478
2. Аналогично при x ®-¥ получим, что асимптота имеет вид y=-5x+9,42478
6) Точки экстремума. Интервалы монотонности.
Производная равна 
 при
при 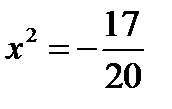 (данное уравнение не имеет вещественных корней), следовательно эта функция монотонна и всё время убывает.
(данное уравнение не имеет вещественных корней), следовательно эта функция монотонна и всё время убывает.
7) Точки перегиба. Интервалы выпуклости и вогнутости.
Вторая производная равна 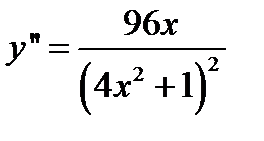
 - точка перегиба
- точка перегиба
При x<0 y’’<0 – функция выпукла
При x>0 y’’>0 – функция вогнута
8) Построение графика.

Дата добавления: 2020-11-29; просмотров: 124; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
