Общая схема решения уравнения методом итераций

Метод итераций для уточнения корней

Рассмотрим самый мощный класс методов уточнения корней уравнений. Его достоинство состоит в том, что основная идея рассматриваемых ниже методов является универсальной при приближенном решении уравнений многих классов.

Так называемые итерационные методы уточнения корней уравнений основаны на математической теории, которую необходимо предварительно рассмотреть.

Метрические пространства и принцип сжимающих отображений

Способ измерения расстояния ρ(х, у) между элементами х и у некоторого множества Х (произвольной природы) называется метрикой. Множество с введенной в нем метрикой ρ становится метрическим пространством, если для любых элементов:

1) ρ(х, у) ≥ 0;

2) ρ(х, у) = 0 тогда и только тогда, когда х совпадает с у;

З) ρ(х, у) = ρ(у, х);

4) ρ(х, у) ≤ ρ( x , z ) + ρ( z , у).

Пусть х(х₁, х_{2, … ,}х _n ) и y ( y _1, y ₂ , …, y_n ) – две точки множества Х.

Расстояние между точками ρ(х, у) чаще всего задается тремя метриками:

1) ρ₁(х, у) = 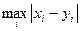(1)

2) ρ₂(х, у) = (2)

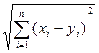3) ρ₃(х, у) = (3)

Пусть F - отображение, действующее в метрическом пространстве Е с метрикой ρ; х и у - точки пространства Е, а F х, F у - образы этих точек.

Отображение F пространства Е в себя называется сжимающим отображением, если существует такое число q : 0 < q < 1, что для любых двух точек х, у 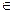Е выполняется неравенство:

ρ(х, у) ≤ q ·ρ( x , y ). (4)

Точка х называется неподвижной точкой отображения F, если отображение переводит ее саму в себя:

F х = х (5)

Важнейшее значение в теории решения уравнений имеет следующая теорема (Принцип сжимающих отображений):

Если F — сжимающее отображение, определенное в полном метрическом пространстве, то для него существует единственная неподвижная точка ξ, такая, которая переводится отображением в себя: ξ = Fξ . Эта точка является пределом последовательности

x ⁽⁰⁾ , x ⁽¹⁾ = Fx ⁽⁰⁾ , x ₂ = Fx ⁽¹⁾ , … , x ⁽ ⁿ ⁺¹⁾ = Fx ⁽ ⁿ ⁾ , … (6)

с любым начальным членом х⁽⁰⁾.

Последовательность (6) называют итерационной последовательностью. Итерационная последовательность, образуемая сжимающим отображением, является сходящейся.

В процессе доказательства этой теоремы получается и оценка расстояния между неподвижной точкой отображения и очередным приближением х⁽ ^k ⁾:

(7)

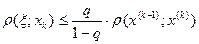, (8)

где q – коэффициент сжатия из условия (4).

Метод простой итерации

Применим принцип сжимающих отображений для уточнения значения корня уравнения. Для этого заменим уравнение (1) равносильным уравнением:

х = φ(х) (9)

Сделать это можно множеством способов. Простейший — добавить х к левой и правой частям уравнения (1).

Пусть х^* — корень уравнения (9), а х₀ — полученное каким - либо способом на этапе отделения корней грубое приближение к корню х^*. Подставляя х₀ в правую часть уравнения (9), получим некоторое число х₁ = φ (х₀). Проделаем то же самое с х₁, получим х₂ = φ (х₁) и т. д. Последовательно применяя рекуррентное соотношение х _n = φ (х _n _-1 ) для n = 1, 2,…, образуем итерационную последовательность, подобную последовательности (6):

x ₀ , x ₁ = φ ( x ₀ ), x ₂ = φ ( x ₁ ), … x_n = φ ( x_n _-1 ), … (10)

Построенная итерационная последовательность приближений может быть как сходящейся, так и расходящейся. Как следует из принципа сжимающих отображений, условием сходимости итерационной последовательности является то, что функция φ (х) осуществляет сжимающее отображение в окрестности корня.

Если существует такое число q : 0 < q < 1, что для любых выполняется неравенство:

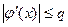, (11)

где 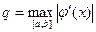, (12)

то функция φ ( x ) является сжимающей на [a ; b].

Условия (11), (12) являются достаточными, но не необходимыми для сходимости итерационной последовательности (10). Это означает, что итерационная последовательность может оказаться сходящейся и при невыполнении этого условия.

Общая схема решения уравнения методом итераций

1. Выполнить отделение корней. Выбрать тот корень, который подлежит уточнению, и соответствующий ему отрезок [a ; b], содержащий этот корень и не содержащий других корней данного уравнения.

2. Преобразовать уравнение (1) к равносильному ему уравнению вида (9).

3. Найти 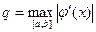и проверить, является ли функция φ ( x ) сжимающей на отрезке [a ; b].

4. Если сжимаемость имеет место, то:

4.1 задаться точностью ξ нахождения приближенного значения корня;

4.2 задаться первым членом итерационной последовательности х₀ – начальным приближением к корню;

4.3 построить следующий член итерационной последовательности (10);

4.4 всякий раз, получив очередной член итерационной последовательности, проверять, выполняется ли условие, следующее из (8):

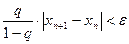или (n = 0, 1, 2,…); (13)

4.5 если условие (13) выполняется, то принять х _n, за результат, иначе вновь выполнить пункт 4.3.

Способ перехода от уравнения в форме (1) к равносильному уравнению в форме (9) (и связанный с этим вид функции φ (х)) является определяющим для сходимости итерационной последовательности. Если подбирать φ (х) вслепую, можно впустую потратить массу времени. Однако есть общие приемы, которые позволяют избежать этой ситуации.

Рассмотрим простейший из них. Преобразуем уравнение (1) к равносильному уравнению

х = х - μ · f ( x ), (14)

где μ - отличная от нуля константа.

Таким образом, φ( x ) = х - μ · f ( x ). Условие (11) приобретает вид

(15)

Если удастся подобрать значение μ так, чтобы условие (15) выполнялось, то метод итераций применим.

Пусть на [a ; b] существует единственный корень уравнения f ( x ) = 0. Будем считать функцию f (х) дифференцируемой на отрезке [a ; b] и сохраняющей на этом отрезке свой знак (фактически предполагается, что отрезок достаточно мал).

Рассмотрим вначале случай, когда . Полагая

, (16)

получим из (14) итерационную формулу:

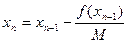(17)

Рассмотрим критерий выхода из итерационного процесса:

= = .

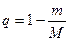Т.к. , то , где .

В случае, когда , путем аналогичных рассуждений получим: и итерационную формулу:

(18)

Одним из важнейших свойств итерационных методов решения уравнений, является свойство самоисправляемости. Поскольку начальное приближение х₀ выбирается произвольно, то отсюда следует, что полученное в итерационном процессе n-е приближение при желании можно считать начальным. Это означает, что если в процессе вычисления приближений допускались ошибки, то они не влияют на окончательный результат (при условии, что запрашиваемая точность результата существенно ниже реализуемого в процессе счета уровня точности представления числовых данных). Указанное свойство метода итераций делает его одним из самых надежных методов решения уравнений.

Дата добавления: 2020-11-27; просмотров: 101; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!