Методы определения точечных статистических оценок
Существуют три метода определения точечных статистических оценок для параметров генеральной совокупности.
Метод аналогий.
Этот метод основан на том, что для параметров генеральной совокупности выбирают такие же параметры выборки, то есть для оценки  ,
,  выбирают аналогичные
выбирают аналогичные
статистики –  ,
,  .
.
Метод наименьших квадратов.
Согласно этому методу, статистические оценки определяются из условия минимизации суммы квадратов отклонений вариант выборки от статистической оценки  . Используя метод наименьших квадратов, можно, например, определить статистическую оценку для
. Используя метод наименьших квадратов, можно, например, определить статистическую оценку для 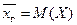 . Для этого воспользуемся функцией
. Для этого воспользуемся функцией  .
.
Используя условие экстремума, получим:

Отсюда, для  точечной статистической оценкой будет
точечной статистической оценкой будет 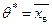 – выборочная средняя.
– выборочная средняя.
Метод максимального правдоподобия.
Этот метод занимает центральное место в теории статистического оценивания параметров. На него в свое время обращал внимание К. Гаусс, а разработал его Р. Фишер. Этот метод рассмотрим подробнее.
Пусть признак генеральной совокупности  определяется только одним параметром
определяется только одним параметром  и имеет плотность вероятностей
и имеет плотность вероятностей  . В случае реализации выборки с вариантами
. В случае реализации выборки с вариантами 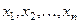 плотность вероятностей выборки будет:
плотность вероятностей выборки будет:
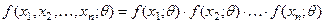 . (9)
. (9)
При этом варианты рассматриваются как независимые случайные величины, имеющие один и тот же закон распределения, и признак генеральной совокупности  .
.
|
|
|
Суть метода заключается в том, что, фиксируя значение вариант  , определяют такие значения параметра
, определяют такие значения параметра  , при котором функция (9) имеет максимум. Она называется функцией максимального правдоподобия и обозначается:
, при котором функция (9) имеет максимум. Она называется функцией максимального правдоподобия и обозначается:  .
.
Например, когда признак генеральной совокупности  имеет нормальный закон распределения, то функция максимального правдоподобия:
имеет нормальный закон распределения, то функция максимального правдоподобия:
 (10)
(10)
При этом вместо статистических оценок  выбирают те значения, при которых функция (10) достигает максимума.
выбирают те значения, при которых функция (10) достигает максимума.
На практике удобно от функции (10) перейти к ее логарифму:
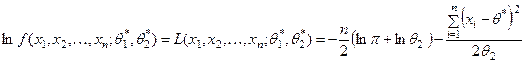 . (11)
. (11)
Согласно необходимому условию экстремума для этой функции получим:
 (12)
(12)
Из первого уравнения системы (12) :
 .
.
Из второго уравнения системы (12):
 Значит, для
Значит, для  точечной статистической оценкой будет
точечной статистической оценкой будет 
Свойства  ,
,  . Исправленная дисперсия, исправленное среднее квадратическое отклонение.
. Исправленная дисперсия, исправленное среднее квадратическое отклонение.
|
|
|
Точечной несмещенной статистической оценкой для  является
является  .
.
Действительно,
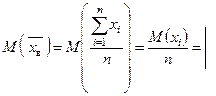 Учитывая, что
Учитывая, что 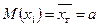

Значит,  .
.
Проверим на несмещенность статистическую оценку  .
.



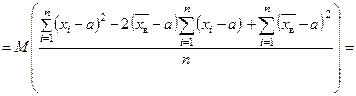
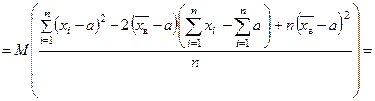


Так как 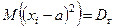 і і  , то , то
|

Таким образом,  .
.
Значит,  является точечной смещенной статистической оценкой для
является точечной смещенной статистической оценкой для  , где
, где  – коэффициент смещения, который уменьшается с увеличением объема выборки
– коэффициент смещения, который уменьшается с увеличением объема выборки  .
.
 .
.
Значит, 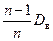 будет точечной несмещенной статистической оценкой для
будет точечной несмещенной статистической оценкой для  . Ее назвали исправленной дисперсией и обозначили через
. Ее назвали исправленной дисперсией и обозначили через 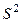 .
.
Отсюда, точечной несмещенной статистической оценкой для  является исправленная дисперсия
является исправленная дисперсия 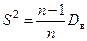 :
:
 . (19)
. (19)
Величину
 (20)
(20)
называют исправленным средним квадратическим отклонением.
Исправленное среднее квадратическое отклонение будет смещенной точечной статистической оценке для 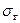 , так как
, так как
 (21)
(21)
где  количество степеней свободы;
количество степеней свободы;  – коэффициент смещения.
– коэффициент смещения.
Пример. Были отшлифованы 200 однотипных деталей. Результаты шлифовки приведены как дискретное статистическое распределение:
|
|
|
 , мм , мм
| 3,7 | 3,8 | 3,9 | 4,0 | 4,1 | 4,2 | 4,3 | 4,4 |

| 1 | 22 | 40 | 79 | 27 | 26 | 4 | 1 |
Найти точечные несмещенные статистические оценки для  ,
,  .
.
Решение. Поскольку точечной несмещенной оценкой для 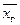 является
является  , то
, то

 мм.
мм.
Для определения точечной несмещенной статистической оценки для  вычислим
вычислим  :
:
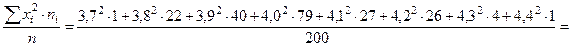

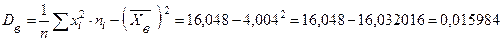 .
.
Тогда точечная несмещенная статистическая оценка для  будет равна:
будет равна:
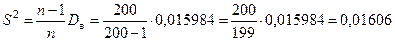 .
.
Дата добавления: 2020-11-27; просмотров: 115; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
