Решение систем дифференциальных уравнений
Лекция 4
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Важное место в математических расчётах занимает решение дифференциальных уравнений. К нему, в частности, обычно относится анализ поведения различных систем во время (анализ динамики), а также вычисление различных полей (тяготения, электрических зарядов и т.д.). Трудно перецинить роль дифференциальных уравнений в моделировании физических и технических объектов и систем.
Maple позволяет решить одиночные дифференциальные уравнения и системы дифференциальных уравнений, как аналитически, так и в численном виде.
Maple содержит специализированные пакеты DEtools и PDEtools для решения и графического представления решений дифференциальных уравнений (обыкновенных и в частных производных соответственно). Однако многие дифференциальные уравнения можно решать, и не подгружая этот пакет, используя функции dsolve и pdesolve, входящие в ядро Maple:
> ode := diff(y(x),x)-y(x)^2+y(x)*sin(x)-cos(x);

> ans := dsolve(ode);

> pdesolve( diff(f(x,y),x,x)+5*diff(f(x,y),x,y)=3, f(x,y) );

Для решения системы простых дифференциальных уравнений (задача Коши) используется функция dsolve в различных формах записи:
dsolve(ODE)
dsolve(ODE, y(x), extra_arqs)
dsolve({ODE, ICs}, y(x), extra_arqs)
dsolve({sysODE, ICs}, {funcs}, extra_arqs)
Здесь ODE – одно обыкновенное дифференциальное уравнение или система из дифференциальных уравнений первого порядка с указанием начальных условий, y(x) – функция одной переменной, ICs – выражение, задающее начальные условия, {sysODE} – множество дифференциальных уравнений, {funcs} – множество неопределённых функций.
|
|
|
Параметр extra_arqs задаёт класс решаемых уравнений. Основными значениями этого параметра являются:
exact – аналитическое решение (принято по умолчанию);
explicit – решение в явном виде;
system – решение системы дифференциальных уравнений;
ICs – решение системы дифференциальных уравнений с заданными начальными условиями;
formal series – решение в форме степенного многочлена;
inteqral transform – решение на основе интегральных преобразований Лапласа, фурье и др;
series – решение в виде ряда с порядком, указанным значением переменной Order
numeric – решение в численном виде.
Решение ОДУ первого порядка
Рассмотрим примеры решения одиночных ОДУ (первого порядка).
> dsolve(diff(y(x),x)-a*x,y(x));

> dsolve(diff(y(x),x)-y(x)=exp(-x),y(x));

Решение ОДУ второго порядка
При решении дифференциального уравнения для задания производной более высоко порядка используется символ $. Ниже приведены решение дифференциального уравнения второго порядка в аналитическом виде:
> de:=m*diff(y(x),x$2)-k*diff(y(x),x);

> yx0:=y(0)=0,y(1)=1;

> dsolve({de,yx0},y(x));

Решение систем дифференциальных уравнений
Для решения таких систем использует функция dsolve(deqns,vars)или dsolve(deqns,vars,option) где
|
|
|
deqns – одно ДУ или система ДУ 1-го порядка с указанием начальных условий;
vars – переменная, относительно которых ищется решение;
option – необязательный параметр, указывающий на метод решения.
Параметр option задаёт один из методов решения:
exact – аналитическое решение (принято по умолчанию);
explicit – решение в явном виде;
laplace – решение через преобразования Лапласа.
Для решения задачи Коши в deqns надо включать начальные условия, а при решении краевых задач – краевые условия. Если Maple способна найти решение при числе начальных или краевых условий меньше порядка системы, то в решении будут появляться неопределённые константы вида _С1, _С2 и т.д. Они же могут быть при аналитическом решении системы, когда начальные условия не заданы. Если решение найдено в неявном виде, то в нём появится параметр _Т.
Производные при записи ДУ могут задаваться функцией diff или оператором D. Выражение deqns должно иметь структуру множества и содержать помимо самой системы уравнений их начальные условия.
Рассмотрим решение системы из двух дифференциальных уравнений различными методами – в явном виде, в виде разложения в ряд и с использованием преобразования Лапласа.
|
|
|
> sys:=diff(y(x),x)=2*z(x)-y(x)-x, diff(z(x),x)=y(x);
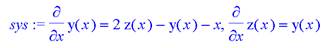
> fcns:={y(x),z(x)};

> dsolve({sys,y(0)=0,z(0)=1},fcns);

> order:=8;dsolve({sys,y(0)=0,z(0)=1},fcns,series);

> dsolve({sys,y(0)=0,z(0)=1},fcns,laplace);

Численное решение ДУ
Для решения дифференциальных уравнений в численном виде используется функция dsolve с параметром numeric или type=numeric. При этом решение возвращается в виде специальной процедуры, по умолчанию реализующей широко известный метод решения дифференциальных уравнений Рунге-Кутта-Фелберга порядков 4 или 5. Эта процедура называется rkf45 и символически выводится (без тела) при попытке решения заданной системы дифференциальных уравнений. Указанная процедура возвращает особый тип данных, позволяющий найти решение в любой точке или построить график решения. При этом используется функция plot[odeplot] из пакета odeplot, предназначенного для визуализации решений ДУ. Процедура имеет особый вид listprocedure и для преобразования листа выходных данных в векторы Y и Z используется функция subs.
В списке параметров функции dsolve можно явным образом включить указание на метод решения: опция method=dverk78 – задаёт решение методом Рунге – Кутта 7 и 8 порядка; опция 'abserr'=aerr – задаёт велияину абсолютной погрешности решения; опция 'minerr'=mine – задаёт минимальную величину погрешности.
|
|
|
Далее приведено решение системы ДУ численным методом.
> restart;
> s:=diff(y1(x),x)=2*sqrt(3*x*x+y1(x)*y1(x)+y1(x)),
diff(y2(x),x)=sqrt(x*x+y1(x)*y1(x)+y2(x));

> f:={y1(x),y2(x)};

> p:=dsolve({s,y1(0)=0,y2(0)=1},f,numeric);

> p(2);

> plots[odeplot](p,[x,y1(x)],0..2.5,labels=[x,y1],color=black);


Решение системы двух ДУ с выводом графика
> restart;
> sys:=diff(y(x),x)=2*z(x)*sin(x)-y(x)-x, diff(z(x),x)=y(x);

> f:={y(x),z(x)};
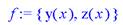
> P:=dsolve({sys,y(0)=0,z(0)=1},f,type=numeric,
output=listprocedure);

> Y:=subs(P,y(x)); Z:=subs(P,z(x));

> plot({Y,Z},0..6);

Дата добавления: 2020-11-27; просмотров: 89; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
