Полиномиальная интерполяция данных
Лекция 2
ОПЕРАЦИИ И ФУНКЦИИ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Вычисление сумм рядов
Для вычисляемой и инертной форм вычисления сумм служат функции:
| Вычисляемая форма: | Инертная форма: |
| sum(f,k) | Sum(f,k) |
| sum(f,k=m..n) | Sum(f,k=m..n) |
где f – функция, задающая члены суммируемого ряда,
k – индекс суммирования,
m и n – целочисленные пределы изменения k.
Значение n может приниматься бесконечным, тогда для n используется константа infinity.
Инертная форма начинается с большой буквы и служит для воспроизведения заданного выражения.
Примеры:
>Sum(k^2, k=1..5)=sum(k^2, k=1..5);
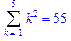
>sum(k^2,k);
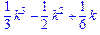
>Sum(1/n!,n=1..infinity)=sum(1/n!,n=1..infinity);
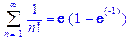
Вычисление произведений
Для вычисления произведений используются функции:
| Вычисляемая форма: | Инертная форма: |
| product(f,k) | Product(f,k) |
| product(f,k=m..n) | Product(f,k=m..n) |
Примеры :
>Product(k^2, k=1..5)=product(k^2, k=1..5);

>product(k^2,k);
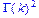
>Product(1/n!,n=1..infinity)=
product(1/n!,n=1..infinity);
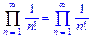
Вычисление производных
Для вычисления производных используются следующие функции:
| Вычисляемая форма: | Инертная форма: |
| diff(f,x1,x2,…,xn) | Diff(f,x1,x2,…,xn) |
| diff(f,[x1,x2,…,xn]) | Diff(f,[x1,x2,…,xn]) |
где f – дифференцируемое алгебраическое выражение, в частности функция f(x1,x2,…,xn) n переменных, по которым производится дифференцирование.
Первая из этих функций вычисляет в простейшем случае diff(f(x),x) первую производную функции f(x) по переменной x. При n>1 вычисления производных выполняются рекурсивно, т.е. diff(f(x),x,y) эквивалентно diff(diff(f(x),x),y). Оператор $ можно использовать для вычисления производных высокого порядка. Для этого после имени соответствующей переменной ставится этот оператор и указывается порядок производной. Например, выражение diff(f(x),x$4) вычисляет производную 4-го порядка и эквивалентно записи diff(f(x),x,x,x,x). А diff(g(x,y),x$2, y$3) эквивалентно diff(g(x,y),x,x,y,y,y).
Примеры :
>Diff(sin(x),x)=diff(sin(x),x);
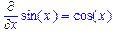
>Diff(x^3+y^2,x,y)=diff(x^3+y^2,x,y);

>Diff(x^6/6!,x$6)=diff(x^6/6!,x$6);
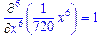
>diff([sin(x),x^n,exp(a*x)],x);
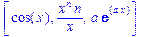
>simplify(%);
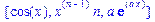
>f(x,y):=cos(x)*y^3;
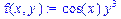
>Diff(f(x,y),x)=diff(f(x,y),x);
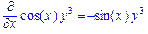
>Diff(f(x,y),x,y)=diff(f(x,y),x,y);
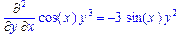
>Diff(f(x,y),[x,y])=diff(f(x,y),[x,y]);
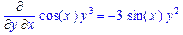
>Diff(f(x,y),x$4)=diff(f(x,y),x$4);
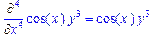
>Diff(f(x,y),x$3,y$2)=diff(f(x,y),x$3,y$2);
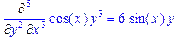
Для вычисления производных может использоваться дифференциальный оператор D. Он позволяет создавать более компактные выражения, чем функции diff и Diff. Дифференциальный оператор может записываться в формах:
D(f) или D[i](f)
где f – выражение или функция,
i – положительное целое число, выражение или последовательность.
Оператор D(f) вычисляет имя производной от f. В форме D(f)(x) этот оператор подобен diff(f(x),x).
>D(sin);
cos
>D(sin)(x)=diff(sin)x,x);
cos(x)=cos(x)
>D(sin)(Pi);
-1
Если f – функция n аргументов, то D[i](f) вычисляет частную производную по отношению к i-му аргументу. В общем случае D[i,j](f) эквивалентно D[i](D[j](f)) и D[](f)=f.
>fun:=(x)->sin(x^2);
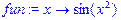
>D(fun);
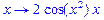
>diff(fun(x),x);
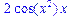
>f:=(x,y,z)->x*exp(y)+ln(z);
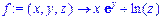
>D[1](f);
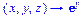
>D[2](f);
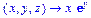
>D[3](f);
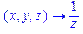
Вычисление интегралов
Для вычисления интегралов используются функции:
| Вычисляемая форма: | Инертная форма: |
| int(f,x) | Int(f,x) |
| int(f,x=a..b) | Int(f,x=a..b) |
| int(f,x=a..b,continuous) | Int(f,x=a..b,continuous) |
где f – подынтегральная функция,
x – переменная интегрирования,
a и b – нижний и верхний пределы интегрирования,
continuous – опционально заданное условие.
Maple старается найти аналитическое значение интеграла. Если это не удается, то возвращается исходная запись интеграла. В этом случае для вычисления определенного интеграла надо использовать функцию evalf(int(f,x=a..b)).
>Int(sin(x),x)=int(sin(x),x);
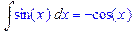
>Int(a*x^n,x)=int(a*x^n,x);
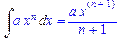
>Int(ln(x)^3,x)=int(ln(x)^3,x);

В отличие от функции дифференцирования, для функции интегрирования нельзя задавать подынтегральную функцию в виде списка или множества, однако возможно вычисление сумм интегралов и интегралов сумм, а также интегралов от полиномов.
>sum(int(x^i,x),i=1..5);
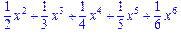
>int(sum(x^i,i=1..5),x);
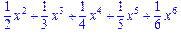
>P(x):=a*x^3+b*x^2+c*x+d;

>int(P(x),x);
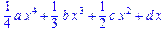
Если Maple не может вычислить интеграл, то можно попытаться найти его значение в виде многочлена
>int(exp(x^4),x);

>convert(taylor(%,x=0,10),polynom);
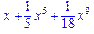
Для вычисления определенных интегралов, необходимо указывать пределы интегрирования.
>Int(x^1.5,x=0..5)=int(x^1.5,x=0..5);
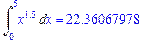
>Int(x*exp(-x),x=0..infinity)=
int(x*exp(-x),x=0..infinity);
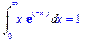
Опция continuous, добавленная в качестве четвертого аргумента команды, вынуждает Maple игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования.
>Int(1/(x-1)^2,x=0..2)=
int(1/(x-1)^2,x=0..2,continuous);
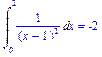
Для вычисления кратных интегралов функции int и Int нужно применять неоднократно:
>Int(Int(x^2*y^2,x),y)=int(int(x^2*y^2,x),y);
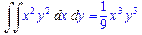
В качестве пределов интегрирования могут быть функции:
>Int(Int(2-x-y,x=sqrt(y)..y^2),y=0..1)=
int(int(2-x-y,x=sqrt(y)..y^2),y=0..1);

Если значение интеграла нельзя найти в аналитическом виде, можно получить его значение с заданной точностью:
>Int(1/(exp(x^2)+x),x=0..1)=
int(1/(exp(x^2)+x),x=0..1);
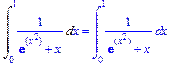
>evalf(%,20);
.58592031278103454744=.58592031278103454744
>evalf(%);
.5859203128=.5859203128
Вычисление пределов функций
Для вычисления пределов функции f в точке x=a используются следующие функции:
| Вычисляемая форма: | Инертная форма: |
| limit(f,x=a) | Limit(f,x=a) |
| limit(f,x=a,dir) | Limit(f,x=a,dir) |
где f – алгебраическое выражение,
x – имя переменной,
dir – опция, указывающая направление поиска предела (left – слева, right – справа, real – в области вещественных значений, complex – в области комплексных значений).
Значением a может быть бесконечность (как положительная, так и отрицательная).
>Limit(1-exp(-x),x=infinity);

>value(%);
1
>Limit(sin(x)^2,x=Pi/2)=limit(sin(x)^2,x=Pi/2);
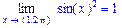
>Limit(exp(x),x=infinity)=limit(exp(x),x=infinity);
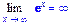
>Limit(exp(x),x=-infinity)=limit(exp(x),
x=-infinity);
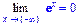
>Limit(1/x,x=0,real)=limit(1/x,x=0,real);

>Limit(tan(x),x=Pi/2,right)=limit(tan(x),x=Pi/2,
right);
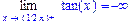
>Limit(tan(x),x=Pi/2,left)=limit(tan(x),x=Pi/2,
left);
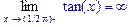
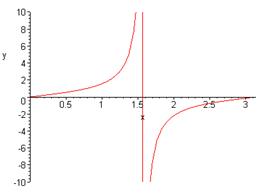
>plot(tan(x),x=0..Pi,y=-10..10);
Разложение функций в ряд
Для разложение функции в ряд служат следующие функции:
series (f,eqn)
series (f,eqn,n)
где f – разлагаемая функция,
eqn – условие (например, в виде x=a) или имя переменной,
n – необязательное и неотрицательное целое число, задающее число членов ряда (по умолчанию n=6, но может переустанавливаться системной переменной Order).
Если в качестве eqn задано имя переменной, это соответствует разложению по этой переменной в области x=0. Задав eqn в виде x=a можно получить разложение по переменной x в окрестности точки x=a.
Разложение получается в форме степенного многочлена. остаточная погрешность задается членом вида O(xn). При точном разложении этот член отсутствует. В общем случае для его удаления можно использовать функцию convert.
>series(sinh(x),x);
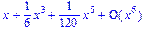
>series(sinh(x),x,10);

>series(2*x^2-x,x=5,10);
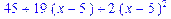
>f:=sin(x)/x;
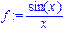
>p:=series(f,x,8);
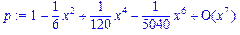
Для разложения в рядТейлора используется функция:
taylor (f,eqn,n)
где f – разлагаемая функция,
eqn – условие (например, в виде x=a) или имя переменной,
n – необязательное и неотрицательное целое число, задающее число членов ряда (по умолчанию n=6).
Задав eqn в виде x=a можно получить разложение по переменной x в окрестности точки x=a. Если в качестве eqn задано имя переменной, то разложение ищется в окрестности точки x=0, т.е. фактически вычисляется рядМаклорена.
>taylor(1-exp(x),x=1,4);

Для разложения в ряд Тейлора функции нескольких переменных используются функции:
mtaylor(f,v)
mtaylor(f,v,n)
mtaylor(f,v,n,w)
где f – разлагаемая функция,
v – список имен или равенств,
n – необязательное число, задающее порядок разложения,
w – необязательный лист целых чисел, задающих «вес» каждой переменной списка v.
Эта функция должна вызываться из библиотека Maple.
>readlib(mtaylor):
>mtaylor(sin(x*y),[x,y],10);

Для вычисления асимптотическихразложений функций (в виде рядов) используются функции:
asympt(f,x)
asympt(f,x,n)
где f – разлагаемая функция,
x – имя переменной, по которой производится разложение,
n – необязательное число, задающее порядок разложения.
>asympt(x/(1-x^2),x);
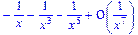
Полиномиальная интерполяция данных
Если данные некоторой зависимости y(x) заданы векторами X и Y её дискретных значений, то для получения интерполяционного степенного многочлена – полинома можно использовать функцию:
| Вычисляемая форма: | Инертная форма: |
| interp(X,Y,v) | Interp(X,Y,v) |
Переменная v указывает имя переменной интерполяционного полинома. Векторы X и Y должны содержать n+1 координат точек исходной зависимости, где n – степень интерполяционного многочлена.
>X:=[1,2,3,4,5]: Y:=[0.3,1,2,2,1]:
>Digits:=5: f:=interp(X,Y,a);
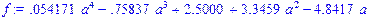
Дата добавления: 2020-11-27; просмотров: 58; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
