Вычисление погрешности эксперимента
Оценки однородных дисперсий нескольких серий параллельных опытов можно усреднить и найти величину
sy2 = 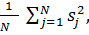 (1.6)
(1.6)
называемой оценкой дисперсии воспроизводимости. С ней связано число степеней свободы j = N ( k -1).
На основании таблицы 2
sy 2 = (1,45 + 0,70 + 0,54)/3 = 0,897.
f = N ( k -1) = 3 (2-1) = 3.
Оценку дисперсии среднего значения рассчитывают по формуле
sy̅2 = sy 2 / k .
С ней также связано число степеней свободы j = N ( k -1).
В рассматриваемом примере 1.1
sy̅2 = 0,897/2 = 0,449.
Если при проведении эксперимента опыты дублируют и пользуются средними значениями функции отклика y, то при обработке экспериментальных данных следует использовать sy̅2. В тех случаях, когда из-за недостатка времени, трудоемкости или высокой стоимости эксперимента опыты не дублируются, при обработке экспериментальных данных используют sy 2 .
ЭКСПЕРИМЕНТАЛЬНО-СТАТИСТИЧЕСКИЕ МОДЕЛИ
Математическое описание
Под математическим описанием процесса будем понимать систему уравнений, связывающих функции отклика с влияющими факторами. В простейшем случае это может быть одно уравнение. Часто математическое описание называют математической моделью.
С помощью математических методов оптимального планирования эксперимента можно получить математическую модель процесса даже при отсутствии сведений о его механизме. Это в ряде случаев бывает очень полезно.
|
|
|
Ценность математического описания заключается в том, что оно:
во-первых, даёт информацию о влиянии факторов;
во-вторых, позволяет количественно определить значения функций отклика при заданном режиме ведения процесса;
в-третьих, может служить основой для оптимизации.
Следует отметить, что на основе методов планирования эксперимента можно количественно описать также свойства таких продуктов, как сплавы, бетоны, сухие строительные смеси, керамика, пластмассы, композитные материалы и т.п.
Математические модели, получаемые с помощью методов планирования эксперимента, принято называть экспериментально-статистическими.
Полный факторный эксперимент
Метод полного факторного эксперимента даёт возможность получить математическое описание исследуемого процесса в некоторой локальной области факторного пространства, лежащей в окрестности выбранной точки с координатами (х01, х02, …, х0 n ).
Перенесем начало координат факторного пространства в выбранную точку (рисунок 3). С этой целью введем новые переменные
Xi = 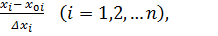 (2.1)
(2.1)
где 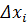 – масштаб по оси Х i.
– масштаб по оси Х i.
Иногда величину Xi называют кодированной переменной.
|
|
|
Рисунок 3 – Введение кодированных переменных
Функцию отклика в окрестности нового начала координат разложим в ряд Тейлора
y = β 0 + β 1 X 1 + β 2 X 2 +…+ βnXn + β 12 X 1 X 2 +…+ β ( n -1) n Xn -1 Xn + β 11 X 1 2 + β 22 X 2 2 +
+ βnn Xn 2 +…, (2.2)
где β 0 = y (0,0,…0) – значение функции отклика в начале координат;



и т.д.
Метод полного факторного эксперимента служит для получения математического описания процесса в виде отрезка ряда Тейлора (2.2). При этом обычно ограничиваются линейной частью разложения и членами, содержащими произведения факторов в первой степени. Таким образом, удается находить уравнение локального участка поверхности отклика, если его кривизна не слишком велика.
Следует отметить, что коэффициенты искомого уравнения определяются на основе экспериментальных данных и, следовательно, несут на себе отпечаток погрешностей эксперимента. Чтобы подчеркнуть это обстоятельство, в уравнении вместо символов β, обозначающих истинные значения коэффициентов, пишут b, подразумевая под этим соответствующие выборочные оценки.
|
|
|
Итак, с помощью полного факторного эксперимента ищут математическое описание процесса в виде уравнения:
y= b0 + b1X1 + b2X2 + … + bnXn + b12X1 X2 + … + b ( n -1) n Xn -1 Xn (2.3)
Его называют уравнением регрессии, а входящие в него коэффициенты - коэффициентами регрессии.
Для удобства вычислений коэффициентов регрессии все факторы в ходе полного факторного эксперимента варьируют на двух уровнях, соответствующих значениям кодированных переменных +1 и -1.
Таким образом, полным факторным экспериментом называется система опытов, содержащая все возможные неповторяющиеся комбинации уровней варьирования факторов.
В таблице 3 приведены условия опытов полного двухфакторного эксперимента. Совокупность чисел во втором и третьем столбцах таблицы называется матрицей планирования.
Таблица 3 - Полный двухфакторный эксперимент
| Номер опыта | Факторы | Функция отклика | |
| Х1 | Х2 | ||
| 1 | -1 | -1 | y1 |
| 2 | +1 | -1 | y2 |
| 3 | -1 | +1 | y3 |
| 4 | +1 | +1 | y4 |
Как видно из рисунка 4, опыты, приведенные в таблице 3, соответствуют на факторной плоскости вершинам квадрата с центром в начале координат.
Рисунок 4 – Опыты полного двухфакторного эксперимента
В таблице 4 приведены условия опытов полного трехфакторного эксперимента. Эти опыты соответствуют в факторном пространстве вершинам куба с центром в начале координат.
|
|
|
Таблица 4 - Полный трехфакторный эксперимент
| Номер опыта | Факторы | Функция отклика | ||
| Х1 | Х2 | Х3 | ||
| 1 2 3 4 5 6 7 8 | -1 +1 -1 +1 -1 +1 -1 +1 | -1 -1 +1 +1 -1 -1 +1 +1 | -1 -1 -1 -1 +1 +1 +1 +1 | у1 у2 у3 у4 у5 у6 у7 у8 |
Из таблиц 3 и 4 видны основные принципы построения матрицы планирования полного факторного эксперимента:
уровни варьирования первого фактора чередуются от опыта к опыту;
частота смены уровней варьирования каждого последующего фактора вдвое меньше, чем у предыдущего.
Матрица планирования полного факторного эксперимента обладает следующими свойствами:
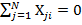 (2.4)
(2.4)
 (2.5)
(2.5)
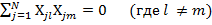 (2.6)
(2.6)
Здесь N - число опытов полного факторного эксперимента;
j - номер опыта;
i, l, m - номера факторов.
Свойство, выраженное уравнением (2.6), называется ортогональностью. Поэтому говорят, что матрица полного факторного эксперимента ортогональна. Это свойство позволяет вычислять коэффициенты регрессии по простым формулам независимо друг от друга.
Общее количество опытов в матрице планирования
N =2 n , (2.7)
где n - число факторов.
На основании полного факторного эксперимента вычисляют коэффициенты регрессии, пользуясь следующими формулами:
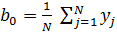 , (2.8)
, (2.8)
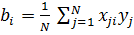 (2.9)
(2.9)
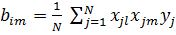 (где l ≠ m) (2.10)
(где l ≠ m) (2.10)
Некоторые из коэффициентов регрессии могут оказаться пренебрежимо малыми - незначимыми. Чтобы установить, значим коэффициент или нет, необходимо прежде всего вычислить оценку дисперсии, с которой он определяется:
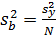 (2.11)
(2.11)
Следует отметить, что с помощью полного факторного эксперимента все коэффициенты определяются с одинаковой погрешностью.
Принято считать, что коэффициент регрессии значим, если выполнено условие
|b| ≥ sb t (2.12)
где t - значение критерия Стьюдента (псевдоним английского математика Госсета). Значения критерия t приведены в Приложении 2.
В противном случае коэффициент регрессии незначим, и соответствующий член можно исключить из уравнения.
Получив уравнение регрессии, следует проверить его адекватность, т. е. способность достаточно хорошо описывать поверхность отклика. Эту проверку осуществляют с помощью критерия Фишера, который представляет собой следующее отношение:
 (2.13)
(2.13)
где s2ад - оценка дисперсии адекватности.
В числителе дроби (2.13) находится бóльшая, а в знаменателе меньшая из указанных оценок дисперсий.
Оценку дисперсии адекватности вычисляют по формуле
 , (2.14)
, (2.14)
где В - число коэффициентов регрессии искомого уравнения, включая и свободный член;
yэj, ypj - экспериментальное и расчетное значение функции отклика в j-м опыте;
N - число опытов полного факторного эксперимента.
С оценкой дисперсии адекватности связано число степеней свободы
fад = N – B . (2.15)
Уравнение регрессии считается адекватным, если выполняется условие
Fp ≤ F , (2.16)
где F - значение критерия Фишера (из Приложения 3).
Для пользования Приложением 3 необходимо знать число степеней свободы, связанных с числителем и знаменателем выражения (2.13).
Пример 2.1
Требуется с помощью полного факторного эксперимента получить зависимость пористости керамического кирпича y от температуры обжига x 1 (°С) и времени изотермической выдержки x 2 (мин) в окрестности точки факторного пространства с координатами х01=1050°С и х02=45 мин.
Решение. Математическое описание рассматриваемого процесса будем искать в виде уравнения регрессии
y = b0 + b1Х1 + b2Х2,
где кодированные переменные связаны с температурой и временем обжига следующими соотношениями
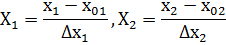
При проведении полного факторного эксперимента зададимся условиями, приведенными в таблице 5.
Таблица 5 - Основные характеристики плана экспериментов
| Характеристика | х1, °С | х2, мин |
| Основной уровень | 1050 | 45 |
| Интервал варьирования | 50 | 15 |
| Верхний уровень | 1100 | 60 |
| Нижний уровень | 1000 | 30 |
Матрица планирования и результаты полного факторного эксперимента представлены в таблице 6.
Таблица 6 - Полный двухфакторный эксперимент
| Номер опыта | Х1 | Х2 | х1, °С | х2, % | ȳ, % |
| 1 | -1 | -1 | 1000 | 30 | 9 |
| 2 | +1 | -1 | 1100 | 30 | 4 |
| 3 | -1 | +1 | 1000 | 60 | 5 |
| 4 | +1 | +1 | 1100 | 60 | 3 |
На основании результатов полного факторного эксперимента рассчитаем коэффициенты регрессии, пользуясь формулами (2.8) и (2.9):



Будем считать, что оценка дисперсии среднего значения s2j определена по методике, изложенной в параграфе 1.3, и равна 0,25. Примем также, что с этой величиной связаны 3 степени свободы.
Ошибку в определении коэффициентов регрессии вычислим по формуле
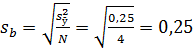
Пользуясь Приложением 3, находим, что для доверительной вероятности Р=0,95 и 3 степеней свободы значение критерия Стьюдента t=3,18.
Тогда
sbt=0,25∙3,18=0,795.
Для оценки значимости коэффициентов регрессии рассмотрим следующие соотношения:
|b0| = 5,25 > sbt;
|b1| = 1,75 > sbt;
|b2| = 1,25 > sbt.
Отсюда видно, что все коэффициенты регрессии значимы. Следовательно, искомое уравнение имеет вид:
у=5,25+1,95Х1-1,35Х2
Для проверки адекватности уравнения регрессии найдем расчетные значения функции отклика:
ур1=35,6+1,95(-1)-1,35(-1) =35,0
ур2=35,6+1,95(+1)-1,35(-1) =38,9
ур3=35,6+1,95(-1)-1,35(+1) =32,3
ур4=35,6+1,95(+1)-1,35(+1) =36,2
По формуле (2.14) вычислим оценку дисперсии адекватности:
 [(35,5-35,0)2 + (38,7 – 38,9)2 + (32,6 – 32,3)2 + (36,2 – 36,2 )2] = 0,38
[(35,5-35,0)2 + (38,7 – 38,9)2 + (32,6 – 32,3)2 + (36,2 – 36,2 )2] = 0,38
С ней связано число степеней свободы f=N-B=4-3=1. Расчетное значение критерия Фишера находим по формуле:

Оно не превосходит значения, приведенного в Приложении 3. Следовательно, уравнение регрессии адекватно.
Пример 2.2
Изучался процесс обжига керамической массы, состоящей из кембрийской глины и кварцевого песка в зависимости от температуры обжига (x1), времени изотермической выдержки (x 2) и содержания добавки кварцевого песка (x3). В качестве переменной состояния на обожженных образцах методом гидростатического взвешивания определялась открытая пористость. В результате анализа научно–технической литературы и проведенных предварительных экспериментов выбрана область определения факторов (таблица 7).
Таблица 7 – План эксперимента, выраженный в натуральных единицах
| Наименование фактора | Обозначение | Ед. изм. | Нулевой уровень фактора | Интервал варьирования | Верхний уровень фактора | Нижний уровень фактора |
| Температура обжига | x 1 | °С | 1000 | 50 | 1050 | 950 |
| Длительность изотермической выдержки | x 2 | мин | 40 | 20 | 60 | 20 |
| Содержание кварцевого песка | x 3 | % масс. | 10 | 5 | 15 | 5 |
Таким образом, в данном случае необходимо воспользоваться планом ПФЭ 23, предполагающим проведение 8 опытов (N = 8). Матрица планирования выглядит следующим образом (таблица 8):
Таблица 8 – План эксперимента ПФЭ 23
| Опыты | Планирование | y | |||
| X0 | X1 | X2 | X3 | ||
| 1 | +1 | +1 | +1 | +1 | y1 |
| 2 | +1 | -1 | +1 | +1 | y2 |
| 3 | +1 | +1 | -1 | +1 | y3 |
| 4 | +1 | -1 | -1 | +1 | y4 |
| 5 | +1 | +1 | +1 | -1 | y5 |
| 6 | +1 | -1 | +1 | -1 | y6 |
| 7 | +1 | +1 | -1 | -1 | y7 |
| 8 | +1 | -1 | -1 | -1 | Y8 |
Полиномиальное уравнение для такого плана в общем виде выглядит следующим образом:
 , (2.17)
, (2.17)
Рабочая матрица ПФЭ 23 представлена в таблице 9.
Таблица 9 – Рабочая матрица ПФЭ 23
| опыт | Планирование | Переменная состояния y, εоткр., % об. | yср. | |||||||
| Тобж. | tвыд. | % SiO2 | y1 | y2 | y3 | y4 | y5 | y6 | ||
| 1 | 1050 | 60 | 15 | 8,8 | 9,4 | 9,0 | 8,9 | 9,1 | 9,4 | 9,1 |
| 2 | 950 | 60 | 15 | 10,5 | 11,8 | 11,2 | 10,8 | 11,1 | 11,2 | 11,1 |
| 3 | 1050 | 20 | 15 | 13,1 | 13,0 | 12,7 | 12,9 | 12,9 | 12,8 | 12,9 |
| 4 | 950 | 20 | 15 | 14,1 | 13,7 | 13,9 | 14,3 | 14,1 | 13,9 | 14,0 |
| 5 | 1050 | 60 | 5 | 14,9 | 14,7 | 15,4 | 15,3 | 14,9 | 15,4 | 15,1 |
| 6 | 950 | 60 | 5 | 17,7 | 17,2 | 16,9 | 17,3 | 17,2 | 17,5 | 17,3 |
| 7 | 1050 | 20 | 5 | 20,1 | 18,7 | 19,4 | 18,5 | 20,0 | 18,5 | 19,2 |
| 8 | 950 | 20 | 5 | 23,3 | 22,9 | 23,7 | 23,1 | 22,9 | 22,7 | 23,1 |
Число параллельных опытов в каждой строке плана равнялось шести (m = 6).
Расчет коэффициентов регрессии по формулам (2.8)-(2.10):
b0 = 1/8 × (9,1+11,1+12,9+14,0+15,1+17,3+19,2+23,1) = 15,2;
b1 = 1/8 × (9,1-11,1+12,9-14,0+15,1-17,3+19,2-23,1) = -1,15;
b2 = 1/8 × (9,1+11,1-12,9-14,0+15,1+17,3-19,2-23,1) = -2,33;
b3 = 1/8 × (9,1+11,1+12,9+14,0-15,1-17,3-19,2-23,1) = -3,46.
Расчет построчных дисперсий по формуле (1.3):
s12 = 1/(6-1) × (0,32 + 0,32 + 0,22 + 0,12 + 02 + 0,32) = 0,32/5 = 0,080;
s22 = 1/(6-1) × (0,62 + 0,72 + 0,12 + 0,32 + 02 + 0,12) = 0,96/5 = 0,192; (max sj2)
s32 = 1/(6–1) × (0,22 + 0,12 + 0,22 + 02 + 02 + 0,12) = 0,1/5 = 0,020;
s42 = 1/(6–1) × (0,12 + 0,32 + 0,12 + 0,32 + 0,12 + 0,12) = 0,22/5 = 0,044;
s52 = 1/(6–1) × (0,22 + 0,42 + 0,32 + 0,22 + 0,22 + 0,32) = 0,45/5 = 0,090;
s62 = 1/(6–1) × (0,42 + 0,12 + 0,42 + 02 + 0,12 + 0,22) = 0,38/5 = 0,076;
s72 = 1/(6–1) × (0,92 + 0,52 + 0,22 + 0,72 + 0,82 + 0,72) = 2,72/5 = 0,544;
s82 = 1/(6–1) × (0,22 + 0,22 + 0,62 + 02 + 0,22 + 0,42) = 0,64/5 = 0,164.
Cумма sj2 = 1,172; sj2 max = 0,192.
Критерий Кохрена расчетный Gp находим по формуле (1.4):
Gp = 0,192/1,172 = 0,1638
Критерий Кохрена G находят по таблицам (Приложение 1) для степеней свободы:
f1 = m – 1 = 5
f2 = N = 8
для уровня значимости Р = 0,05 критерий G = 0,4387.
Условие Gp < G выполняется, следовательно, построчные дисперсии однородны и их можно усреднить:
s02 = 1,172 / 8 = 0,1465.
Проверка значимости коэффициентов регрессии.
Вычисляем дисперсию коэффициентов регрессии (bi), которая принимается равной для всех bi, по формуле (2.11):
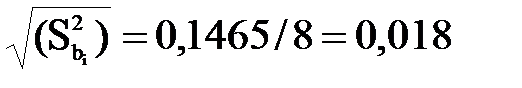
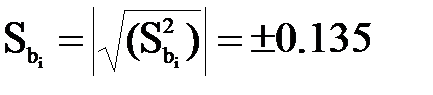
1–й способ. Используется проверка по критерию Стьюдента, расчетное значение коэффициента которого вычисляется по формуле (2.18):
 (2.18)
(2.18)
Табличное значение коэффициента Стьюдента (tт) находят по числу степени свободы fo = N (m – 1) и уровню значимости q= 0,05 (Приложение 2).
Для каждого bi выполняется условие:
tiр > tт
следовательно, все коэффициенты регрессии оказались значимыми.
2–й способ. Используется доверительный интервал D bi , который вследствие равенства s2bi для всех коэффициентов, одинаков для всех bi :
D bi = ± tт sbi (2.19)
Значимость коэффициентов регрессии оцениваем, сравнивая абсолютные значения коэффициента и доверительного интервала:
½ bi ½ >½ D bi½ . (2.20)
Оба условия (по двум способам) выполняются, следовательно, все коэффициенты регрессии являются значимыми. Уравнение регрессии для данного примера выглядит следующим образом:

Проверка адекватности уравнения регрессии.
Для расчета дисперсии адекватности необходимо вычислить значения y по полученному уравнению регрессии и найти Dyi = yiэ – yiр (таблица 10).
Таблица 10 – Расчет погрешности предсказанных и экспериментальных значений функции отклика
| Опыт | yэксп | yрасч | Dy | Dy2 |
| 1 | 9,1 | 8,29 | 0,81 | 0,66 |
| 2 | 11,1 | 10,59 | 0,51 | 0,26 |
| 3 | 12,9 | 12,94 | –0,04 | 0,001 |
| 4 | 14,0 | 15,24 | –1,24 | 1,53 |
| 5 | 15,1 | 15,21 | –0,11 | 0,01 |
| 6 | 17,3 | 17,51 | –0,21 | 0,05 |
| 7 | 19,2 | 19,86 | –0,66 | 0,44 |
| 8 | 23,1 | 22,16 | 0,94 | 0,88 |
S Dy2 = 2,911
Дисперсия адекватности s2ад рассчитывается по формуле (2.21):
 , (2.21)
, (2.21)
где r – число членов в уравнении регрессии, оставшихся после оценки значимости коэффициентов регрессии (r = 4).
s2ад = [1/(8 – 4)] × 2,911 = 0,7278
Адекватность проверяется с помощью критерия Фишера, расчетное значение которого (Fр) определяем по формуле (2.22):
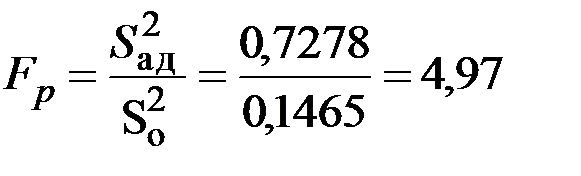 . (2.22)
. (2.22)
Табличное значение коэффициента Фишера (Fт) находим по числу степеней свободы fo и fад. и уровню значимости P (приложение 3).
fo = N = 8; fад = N – r = 4; Fт = 6,04.
Условие Fр < Fт выполняется, уравнение регрессии признается адекватным.
Полученное в результате реализации плана уравнение регрессии в случае его адекватности следует использовать для поиска оптимума сочетаний факторов с применением различных методов оптимизации. Наиболее подходящим в таких случаях является метод крутого восхождения (будет рассмотрен ниже), заключающийся, в общих чертах, в постановке нового плана ПФЭ с другими значениями факторов, приводящих к приближению к экстремуму.
Метод дробных реплик
С увеличением количества факторов резко возрастает количество опытов полного факторного эксперимента. Это видно из уравнения (2.7). Однако для нахождения коэффициентов регрессии не всегда требуется много опытов. В таких случаях можно уменьшить объем экспериментальных работ, воспользовавшись методов дробных реплик.
Рассматриваемый метод заключается в том, что для нахождения математического описания процесса используется определенная часть полного факторного эксперимента: ½, ¼ и т. д. Эти системы опытов называются дробными репликами (см. таблицу 11)
Таблица 11 - Полный трехфакторный эксперимент и его дробные реплики
| Номер опыта | Факторы | Функция отклика | Дробные реплики | |||
| Х1 | Х2 | Х3 | ||||
| 1 | -1 | -1 | -1 | у1 | 1/4 | 1/2 |
| 2 | +1 | -1 | -1 | у2 | ||
| 3 | -1 | +1 | -1 | у3 | 1/4 | |
| 4 | +1 | +1 | -1 | у4 | ||
| 5 | -1 | -1 | +1 | у5 | 1/4 | 1/2 |
| 6 | +1 | -1 | +1 | у6 | ||
| 7 | -1 | +1 | +1 | у7 | 1/4 | |
| 8 | +1 | +1 | +1 | у8 | ||
Расчет коэффициентов регрессии, проверка значимости коэффициентов и адекватности математического описания в данном случае производятся так же, как и при полном факторном эксперименте.
Пусть, например, требуется найти коэффициенты уравнения регрессии
y=b0+b1Х1+b2Х2+b3Х3
Если для этой цели воспользоваться полным трехфакторным экспериментом, то необходимо провести 8 опытов. Однако эту задачу можно решить и с помощью меньшего количества опытов. Например, возьмем матрицу полного двухфакторного эксперимента (таблица 12) и приравняем произведение Х1Х2 к фактору Х3.
Пользуясь формулой (2.8), вычислим
b0= ¼(y1+y2+y3+y4)
С помощью формулы (2.9) найдём:
b1= ¼(-y1+y2-y3+y4)
b2= ¼(-y1-y2+y3+y4)
Таблица 12 - Планирование типа 23-1
| Номер опыта | х1 | х2 | х1х2 | х3 | Функция отклика |
| 1 | -1 | -1 | +1 | +1 | у1 |
| 2 | +1 | -1 | -1 | -1 | у2 |
| 3 | -1 | +1 | -1 | -1 | у3 |
| 4 | +1 | +1 | +1 | +1 | у4 |
Отметим, что в таблице 12 столбцы для произведения Х1Х2 и фактора Х3 полностью совпадают. Поэтому коэффициенты b12 и b3 не могут быть определены раздельно. С помощью формулы (2.9) может быть найдена только их сумма
b12+b3= ¼(y1-y2-y3+y4)
Это недостаток рассматриваемого плана является своеобразной “платой” за уменьшение общего количества опытов с 8 до 4. Такое планирование эксперимента, когда некоторые из факторов приравнивают к произведениям нескольких факторов, называется планирование со смешиванием. Его обозначают символом 2n-p, где n - общее число факторов, а p - число факторов, приравненных к произведениям. С этой точки зрения в таблице 12 приведена матрица планирования 23-1.
Существует правило, позволяющее определить, какие коэффициенты регрессии определяются совместно при планировании со смешиванием. Рассмотрим это правильно на конкретном примере.
Пример 2.3. Методом дробных реплик будем искать математическое описание процесса в виде уравнения регрессии:
y = b0 + b1X1 + b2X2+ b3X3 + b4X4
Воспользуемся планированием типа 25-2 и примем:
X 4 = - X 1 X 2 ;
X 5 = X 1 X 2 X 3 .
Такие равенства в методе дробных реплик называются генерирующими соотношениями. Следует отметить, что выбор генерирующих соотношений в общем случае произволен. Однако он существенно влияет на характер совместных оценок коэффициентов регрессии.
Правило определения совместных оценок коэффициентов состоит в следующем:
1. Прием во внимание, что
X2i=1 ;
Xi•1=Xi .
2. Умножив обе части генерирующих соотношений соответственно на X 4 и X5, получим:
1= - X 1 X 2 X 4 ;
1= X 1 X 2 X 3 X 5 .
Эти равенства называются определяющими контрастами. Перемножив их почленно, получим новые определяющие контрасты. В данном случае это
1= - X 3 X 4 X 5 .
3. Составим алгебраическую сумму из единицы и правых частей всех полученных определяющих контрастов:
S=1 - Х1Х2Х4 + Х1Х2Х3Х5 - Х3Х4Х5.
4. Умножив каждый из факторов на S и заменив факторы соответствующими коэффициентами разложения в ряд Тейлора (2.2), получим
b1 -> β1- β24+ β235- β1345 ;
b2 -> β2- β14+ β135- β2345 ;
b3 -> β3- β1234+ β125- β45 ;
b4 -> β4- β12+ β12345- β35 ;
b5 -> β5- β1245+ β123- β31.
Дата добавления: 2020-11-23; просмотров: 302; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
