ПОТЕНЦИАЛЬНЫЕ И ВЕКТОРНЫЕ ПОЛЯ.
ФОРМУЛА ОСТРОГРАДСКОГО – ГАУССА.
Пусть  - область. В G задано векторное поле
- область. В G задано векторное поле  .
.
В декартовой системе координат  .
.
Df.1  , т.е. существуют все частные производные
, т.е. существуют все частные производные  и они непрерывны в G .
и они непрерывны в G .
Df.2 Дивергенцией (расходимостью) векторного поля  в точке M ( x , y , z ) называется скаляр:
в точке M ( x , y , z ) называется скаляр:
 (1)
(1)
Отметим, что операция  ставит в соответствие векторному полю
ставит в соответствие векторному полю  скалярное поле
скалярное поле  , определенное в G.
, определенное в G.
Дивергенция в заданной точке характеризует мощность источников и стоков в данной точке.
Те точки, где  > 0 называются источниками поля, а те где
> 0 называются источниками поля, а те где  < 0 – стоками.
< 0 – стоками.





Абсолютная величина дивергенции характеризует производительность (интенсивность) источников и стоков. Если  , то в точке М нет ни источника, ни стока.
, то в точке М нет ни источника, ни стока.
Th.1 ( ОСТРОГРАДСКОГО - ГАУССА )
Пусть область  можно представить в виде объединения конечного числа областей
можно представить в виде объединения конечного числа областей  , каждая из которых является одновременно:
, каждая из которых является одновременно:
 -цилиндром,
-цилиндром,  - цилиндром и
- цилиндром и  -цилиндром, тогда
-цилиндром, тогда  - кусочно-замкнутая гладкая поверхность. ограничивающая G . Поле
- кусочно-замкнутая гладкая поверхность. ограничивающая G . Поле  .
.
Тогда справедлива формула Остроградского – Гаусса:
 (2)
(2)
* Причем, поверхностный интеграл берется по внешней стороне поверхности.
Доказательство:
Скалярный вид формулы Остроградского – Гаусса:
|
|
|
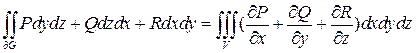 (3)
(3)
Пусть в G z- цилиндроид, т.е.:
 .
.

Тогда:  -гладкие.
-гладкие.
Докажем формулу:
 (4)
(4)
 =
=  (по теореме 5 и формуле (9))=
(по теореме 5 и формуле (9))=  .
.
Пусть теперь G является также и  - цилиндроидом и
- цилиндроидом и  -цилиндроидом. Тогда аналогично можно показать, что:
-цилиндроидом. Тогда аналогично можно показать, что:
 (5)
(5)
 (6)
(6)
Суммируя (4), (5) и (6) получим (3).
Пусть теперь G – объединение областей указанного типа:  .
.
 П
П







 - гладкая.
- гладкая.  тогда:
тогда:
 (*)
(*)
 (**)
(**)
 - две стороны одной поверхности (с нормалями
- две стороны одной поверхности (с нормалями  ). Отсюда скалывая, получим:
). Отсюда скалывая, получим:
|
|
|
 формула (2).
формула (2).
Заметим, что теорема Остроградского – Гаусса справедлива для областей более общего вида.
СЛЕДСТВИЕ.


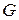
 - область,
- область,  инвариантен относительно системы координат, т.е. не зависит от выбора системы координат.
инвариантен относительно системы координат, т.е. не зависит от выбора системы координат.
Доказательство:
 . Пусть
. Пусть  - открытая область, для которой верна теорема Остроградского – Гаусса.
- открытая область, для которой верна теорема Остроградского – Гаусса.  ,
,  - замкнутая поверхность. ограничивающая H . Тогда:
- замкнутая поверхность. ограничивающая H . Тогда:

По теореме о среднем для кратных интегралов:
 .
.
Отметим, что  , т.к.
, т.к.  .
.
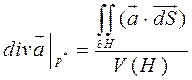 (***)
(***)
Перейдем в (***) к  при
при  . В силу непрерывности
. В силу непрерывности  , получим:
, получим:
 (7)
(7)
Т.к. поток  и
и  не зависят от системы координат
не зависят от системы координат 
 не зависит от выбора системы координат. Из (7)
не зависит от выбора системы координат. Из (7)  физический смысл
физический смысл  . Пусть
. Пусть  - скорость жидкости.
- скорость жидкости.  - средняя объемная плотность потока жидкости через поверхность
- средняя объемная плотность потока жидкости через поверхность  , ограничивающая область H с объемом V .
, ограничивающая область H с объемом V .
 - плотность источника в точке
- плотность источника в точке  .
.
Из (7)  , что при
, что при  > 0 – сток,
> 0 – сток,  =0 – источник отсутствует.
=0 – источник отсутствует.
Таким образом  в какой-нибудь точке равен потоку векторного поля через бесконечно малую замкнутую поверхность, окружающую данную точку, отнесенному к единице объема.
в какой-нибудь точке равен потоку векторного поля через бесконечно малую замкнутую поверхность, окружающую данную точку, отнесенному к единице объема.
Df.2 Пусть  определено в G,
определено в G,  называется соленоидальным в G, если
называется соленоидальным в G, если  .
.
|
|
|
Th.2 (НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ
СОЛЕНОИДАЛЬНОСТИ ПОЛЯ  )
)
Пусть G – область, для которой возможно применение формулы Остроградского – Гаусса.  - замкнутая кусочно-гладкая,
- замкнутая кусочно-гладкая, 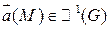 , тогда
, тогда  соленоидально
соленоидально  в G .
в G .
Доказательство:
Необходимость:
Пусть  соленоидально в G
соленоидально в G 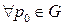 . Пусть
. Пусть  - область допускающая применение формулы Остроградского – Гаусса. Тогда по (7):
- область допускающая применение формулы Остроградского – Гаусса. Тогда по (7):
 в G .
в G .
Достаточность:
Пусть 
 . Пусть
. Пусть  - допускает применение формулы Остроградского – Гаусса, по ней:
- допускает применение формулы Остроградского – Гаусса, по ней:
 соленоидальное.
соленоидальное.
ФОРМУЛА СТОКСА.
Df.1 Пусть  ,
, 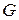 - область, векторное поле
- область, векторное поле  . Ротором (вихрем) векторного поля
. Ротором (вихрем) векторного поля  называется:
называется:
 (1)
(1)
(1) операторная форма записи  . Для того, чтобы получить обычную запись необходимо рассмотреть определитель. При этом нужно понимать:
. Для того, чтобы получить обычную запись необходимо рассмотреть определитель. При этом нужно понимать:
 и т.д. Тогда:
и т.д. Тогда:

Очевидно, операция  ставит в соответствие векторному полю
ставит в соответствие векторному полю  векторное поле
векторное поле  , определенное в G.
, определенное в G.
Th.1 (ТЕОРЕМА СТОКСА)
Пусть  , G – область.
, G – область.  - кусочно-гладкая;
- кусочно-гладкая;  - кусочно-замкнутый контур, ограничивающий П. Тогда:
- кусочно-замкнутый контур, ограничивающий П. Тогда:
 (3)
(3)
(3) – формула Стокса.
(Б/д).
|
|
|








 |  | ||


 | |||
 | |||








При этом сторона поверхности и направление обхода контура  согласованы. Как правило, обычно выбирается внешняя сторона П.
согласованы. Как правило, обычно выбирается внешняя сторона П.
Th.2 (ТЕОРЕМА ГРИНА)
Пусть  ,
,  - область,
- область,  - кусочно-гладкая граница D , ориентированная против часовой стрелки;
- кусочно-гладкая граница D , ориентированная против часовой стрелки;  , тогда:
, тогда:
 (4)
(4)
(4) – формула Грина.
(Б/д).
Покажем, что (4) – есть частный случай формулы Стокса. Причем это нельзя считать доказательством, т.к. при доказательстве (3) используется (4).
Итак: плоскость П зададим так: 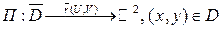 .
.




D 

Тогда  , кроме того
, кроме того  .
.

Из (3) 
 (по теореме о сведении поверхностного интеграла II-го рода к двойному)
(по теореме о сведении поверхностного интеграла II-го рода к двойному)
Здесь  , очевидно
, очевидно  , т.е. С=1. Итак:
, т.е. С=1. Итак:

СЛЕДСТВИЕ ИЗ Th .1
Пусть 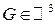 , G-область,
, G-область,  определен в G и инвариантен относительно системы координат.
определен в G и инвариантен относительно системы координат.
 Доказательство:
Доказательство:




 Г
Г
D ●  G
G
 ●
● 
Рассмотрим  направление, задаваемое
направление, задаваемое  . П – плоскость, перпендикулярная
. П – плоскость, перпендикулярная  , проходящая через точку
, проходящая через точку  .
.
Пусть D – поверхность:  .
.
Г – граница (кусочно-гладкая) поверхности D. Направление обхода D согласовано с  . Применим формулу Стокса для поверхности D с нормалью
. Применим формулу Стокса для поверхности D с нормалью  и границей Г:
и границей Г:

где  =
=  ,
,  - проекция
- проекция  на направление
на направление  . По теореме о среднем для поверхностного интеграла I-го рода:
. По теореме о среднем для поверхностного интеграла I-го рода:
 , что
, что
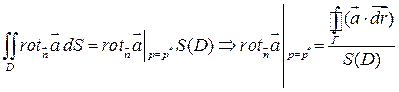 (*)
(*)
Отметим, что 
 - непрерывное векторное поле.
- непрерывное векторное поле.
Перейдем в (*) к пределу при 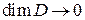 (
(  ,
,  ). В силу непрерывности
). В силу непрерывности  найдем:
найдем:
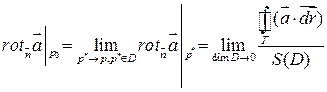
Т.к.  и
и  не зависят от выбора системы координат, то
не зависят от выбора системы координат, то 
 не зависит от выбора системы координат
не зависит от выбора системы координат 
 инвариантен относительно выбора системы координат. (Достаточно взять три неколлинеарных вектора
инвариантен относительно выбора системы координат. (Достаточно взять три неколлинеарных вектора  и считать, что
и считать, что  , проекции
, проекции  на
на  . Есть его координаты).
. Есть его координаты).
СЛЕДСТВИЕ 2.
Пусть  (т.е.
(т.е.  и они непрерывны в G)
и они непрерывны в G)  определяет соленоидальное поле в G, т.е.
определяет соленоидальное поле в G, т.е.  .
.
САМОСТОЯТЕЛЬНО.
Действительно  .
.
 :
: 
§ 5. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА II-ГО РОДА ОТ ФОРМЫ ПУТИ ИНТЕГРИРОВАНИЯ.
ПОТЕНЦИАЛЬНЫЕ И ВЕКТОРНЫЕ ПОЛЯ.
Пусть векторное поле  непрерывно в G;
непрерывно в G;  /
/
Df.1 Выражение 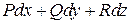 (1) называется полным дифференциалом в G, если
(1) называется полным дифференциалом в G, если  , что:
, что:
 (2)
(2)
т.к.  , то (1) – полный дифференциал
, то (1) – полный дифференциал  если
если  и
и
 (3)
(3)
Напомним, что для  :
:
 (4)
(4)
тогда очевидна следующая Лемма:
(1) – полный дифференциал  и
и  .
.
Доказательство следует из (3) и (4).
Имеют место следующие утверждения:
1)  полный дифференциал в G.
полный дифференциал в G.
2)  , что
, что 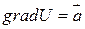 .
.
3)  не зависит от формы пути,
не зависит от формы пути,  - кусочно-гладкая.
- кусочно-гладкая.
4)  - замкнутого кусочно-гладкого,
- замкнутого кусочно-гладкого,  :
:

Df.2 G- область. Обозначим D – область в G,  - граница области (замкнутый простой контур в
- граница области (замкнутый простой контур в  или поверхность в
или поверхность в  ). Тогда G – односвязная
). Тогда G – односвязная  .
.
 Односвязное
Односвязное







 G D
G D
G
Неодносвязное
Th.1 Пусть векторное поле  определено в односвязной области G,
определено в односвязной области G,  , тогда условия (1), (2), (3) и (4) равносильны.
, тогда условия (1), (2), (3) и (4) равносильны.
Доказательство:
Для доказательства введем два вспомогательных утверждения:
(3’)  - ломанной,
- ломанной,  не зависит от формы пути.
не зависит от формы пути.
(4’)  - замкнутой простой ломанной,
- замкнутой простой ломанной,  .
.
Доказательство проведем по следующей схеме:

(1)
(3’) (4’)
Отсюда будет следовать, что все условия эквивалентны.
Отметим, что (1)  (2) доказано Леммой. Далее ограничимся рассмотрением плоского случая, т.е.
(2) доказано Леммой. Далее ограничимся рассмотрением плоского случая, т.е.  .
.
а) (1)  (3)
(3)
Дано: 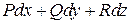 - полный дифференциал, т.е.
- полный дифференциал, т.е.  , что
, что  .
.

 ●
● 
 ●
●

Пусть  - гладкая кривая.
- гладкая кривая.  .
.

 =
=  =
= 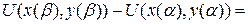
=  .
.
Пусть теперь  - кусочно-гладкая:
- кусочно-гладкая:



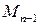



+ 
 .
.
Таким образом, также дается формула вычисления  , если подынтегральное выражение полный дифференциал.
, если подынтегральное выражение полный дифференциал.
б) (3)  (4)
(4)
Пусть 
 не зависят от формы пути. Рассмотрим любой контур Г – замкнутый кусочно-гладкий,
не зависят от формы пути. Рассмотрим любой контур Г – замкнутый кусочно-гладкий,  .
.




 ●
●
 ● ●
● ● 
 ●
●
По свойству кратного интеграла II-го рода  не зависит от начальной точки.
не зависит от начальной точки.  , тогда:
, тогда:  .
.
в) (4)  (4’)
(4’)
Это очевидно, т.к. замкнутая ломанная – частный случай кусочно-гладкой кривой.
г) (4’)  (3’)
(3’)
Ограничимся случаем непересекающихся ломанных.







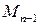


Дано:  - замкнутой ломанной
- замкнутой ломанной  .
.
Доказать:  - ломанной, соединяющей A и B
- ломанной, соединяющей A и B  не зависит от формы пути.
не зависит от формы пути.
Пусть  - две произвольные ломанные, тогда:
- две произвольные ломанные, тогда:
 разобьем:
разобьем: 
 .
.
Можно доказать, что все останется в силе, если ломанные пересекаются.
д) (3’)  (1)
(1)
Дано:  - ломанной,
- ломанной,  не зависит от формы пути.
не зависит от формы пути.
Доказать: что 
Доказательство существования проведем построением.




 ● ●
● ● 
0 x
 , т.к. G открыто, то
, т.к. G открыто, то  , что
, что
 . Возьмем
. Возьмем  . Определим
. Определим 
=  . Это можно сделать, т.к. интеграл не зависит от формы пути и при фиксированной точке А зависит только от конечной точки В( x , y ).
. Это можно сделать, т.к. интеграл не зависит от формы пути и при фиксированной точке А зависит только от конечной точки В( x , y ).
Найдем:

= 
 .
.

Т.к. Р( x , y ) непрерывная в G следовательно по теореме о среднем:
 , причем при
, причем при  ,
, 

 .
.
Аналогично показывается, что  полный дифференциал.
полный дифференциал.
СЛЕДСТВИЕ.
Доказательство теоремы позволяет установить метод отыскания U ( x , y , z ).
Пусть  .
.

 ●
● 
● 

● ●



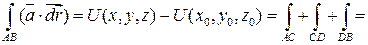
 +
+
 .
.



Df.3 Векторное поле  , определенное в G, называется потенциальным, если оно удовлетворяет любому из равносильных условий (1), (2), (3) и (4); U называют потенциалом (потенциальной функцией) поля
, определенное в G, называется потенциальным, если оно удовлетворяет любому из равносильных условий (1), (2), (3) и (4); U называют потенциалом (потенциальной функцией) поля  .
.
Очевидно, что U ( M ) определяется с точностью до константы.
Th.2 Пусть  , G – односвязная область. Тогда
, G – односвязная область. Тогда  потенциально в G
потенциально в G  .
.
Доказательство:
Необходимость.
Пусть  потенциально в G.
потенциально в G.  - замкнутая кусочно-гладкая граница:
- замкнутая кусочно-гладкая граница:  .
.
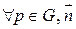 - произвольный нормальный вектор из точки
- произвольный нормальный вектор из точки  к плоскости, содержащей кривую Г.
к плоскости, содержащей кривую Г.




 ●
● 
По инвариантному определению  :
:

Т.к.  произвольного направления, то пусть
произвольного направления, то пусть 
 .
.
Достаточность.
Пусть  .
.  - замкнутой
- замкнутой  - поверхность, что
- поверхность, что  (по теореме Стокса)
(по теореме Стокса) 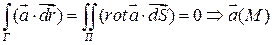 - потенциально.
- потенциально.
Df.4 Пусть векторное поле  называется бизвихревым в G
называется бизвихревым в G  если
если  .
.
Тогда теорему 2 можно переформулировать (перефразировать) следующим образом:
 - потенциальное
- потенциальное  безвихревое.
безвихревое.
Таким образом, отсутствие вихрей является и необходимым и достаточным условием потенциальности поля.
Следует отметить, что необходимым и достаточным условием потенциальности поля является также равенство нулю циркуляции поля по любому замкнутому контуру.
Следует иметь ввиду, что приведенные выше рассуждения справедливы только в случае, когда поле  определено во всех внутренних точках контура Г. Если же хотя бы в одной внутренней точке некоторого замкнутого контура поле
определено во всех внутренних точках контура Г. Если же хотя бы в одной внутренней точке некоторого замкнутого контура поле  не определено, то циркуляция по этому контуру может и не обращаться в нуль, хотя поле и потенциально.
не определено, то циркуляция по этому контуру может и не обращаться в нуль, хотя поле и потенциально.
Рассмотрим еще одно векторное поле – так называемое соленоидальное, или трубчатое поле.
Df.5 Поле вектора  называется соленоидальным или трубчатым, если в каждой точке поля
называется соленоидальным или трубчатым, если в каждой точке поля  .
.
Или имея в виду физический смысл  , можно сказать, что соленоидальное поле – это такое поле, в котором нет источников и стоков.
, можно сказать, что соленоидальное поле – это такое поле, в котором нет источников и стоков.
Примером соленоидального поля является поле вихря вектора  .
.

Основное свойство соленоидального поля состоит в том, что в нем векторные линии не могут нигде ни начинаться, ни кончаться, они могут уходить в бесконечность или быть замкнутыми.
ПРИМЕР.
Проверить на потенциальность поле:  . Найти потенциал и вычислить
. Найти потенциал и вычислить  , где
, где  и
и  .
.
Решение:
Очевидно,  - имеют производные любого порядка в
- имеют производные любого порядка в  , т.е.
, т.е.  .
.
а) Проверка потенциальности:
 =
=  поле потенциально.
поле потенциально.
б) Определяем потенциал:
 1 способ.
1 способ.
z
● 

 ● ●
● ● 

 =
=  , где
, где  .
.
2 способ.
 ;
;

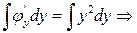
 ;
;
 ;
;
Итак:
 .
.
в)  .
.
§ 6. ВЕКТОРНЫЕ ОПЕРАЦИИ II-ГО ПОРЯДКА.
СИМВОЛИКА ГАМИЛЬТОНА.
В предыдущих параграфах мы ввели понятия: вектора  , характеризующего скорость изменения скалярного поля; производную по направлению
, характеризующего скорость изменения скалярного поля; производную по направлению  , характеризующую скорость изменения величины
, характеризующую скорость изменения величины  в направлении l; скаляра
в направлении l; скаляра  , вектора
, вектора  , характеризующих плотность источников и вращательную способность векторного поля. Были указаны формулы для вычисления этих величин в декартовых координатах.
, характеризующих плотность источников и вращательную способность векторного поля. Были указаны формулы для вычисления этих величин в декартовых координатах.
Пусть  - скалярное поле,
- скалярное поле,  - векторное поле.
- векторное поле.
1) 

Где  - единичный вектор в направлении
- единичный вектор в направлении  .
.
2)  - скаляр.
- скаляр.
3)  - вихрь вектора
- вихрь вектора  , являющийся вектором.
, являющийся вектором.
Известным английским математиком Гамильтоном было замечено, что все эти (и многие другие) операции можно записать кратко при помощи следующего символического вектора – оператора  (читается «набла», оператор Гамильтона).
(читается «набла», оператор Гамильтона).

Проекции символического вектора оператора Гамильтона – суть.
 .
.
Сам вектор  не имеет реального смысла, но результат его применения, как оператора к скалярным или векторным функциям (величинам) дает вполне реальную физическую величину.
не имеет реального смысла, но результат его применения, как оператора к скалярным или векторным функциям (величинам) дает вполне реальную физическую величину.
Тогда символически (обращаясь с  как с вектором в прямоугольной декартовой системе координат и понимая запись
как с вектором в прямоугольной декартовой системе координат и понимая запись  ) операции 1), 2), 3) которые называют операциями I-го порядка можно записать в виде:
) операции 1), 2), 3) которые называют операциями I-го порядка можно записать в виде:
1) 

Таким образом, под символическим произведением вектора  на скаляр
на скаляр  понимается вектор
понимается вектор  с координатами:
с координатами:

2) 

3) Найдем векторное произведение символического вектора:
 на вектор
на вектор  - есть вектор.
- есть вектор.



 =
=
=  - это вектор, который называют вихрем поля
- это вектор, который называют вихрем поля  .
.  от английского слова
от английского слова  - вращение.
- вращение.
Производную по направлению можно записать в виде:
 и вообще
и вообще  .
.
Таким образом, операции первого порядка могут быть единообразно записаны с помощью символического вектора набла.

УТВЕРЖДЕНИЕ. Векторные операции I-го порядка линейны относительно своих аргументов.
Доказательство:
Следует из линейности дифференцирования и скалярного и векторных произведений.
НАПРИМЕР.
 и
и 

Заметим также, что соотношения, содержащие  не зависят от выбора системы координат (это доказано для
не зависят от выбора системы координат (это доказано для  ).
).
Многие формулы векторного анализа легко выводятся при использовании символического вектора  . Нужно понимать, что на функции и векторы, стоящее справа от
. Нужно понимать, что на функции и векторы, стоящее справа от  , этот оператор действует как дифференциальный, а функции и векторы, стоящие слева от
, этот оператор действует как дифференциальный, а функции и векторы, стоящие слева от  , перемножаются с
, перемножаются с  как с обычным вектором по правилам векторной алгебры. В результате такого умножения получается новый дифференциальный оператор.
как с обычным вектором по правилам векторной алгебры. В результате такого умножения получается новый дифференциальный оператор.
Применяя, оператор  к произведениям векторов и скаляров, будем пользоваться следующим правилом:
к произведениям векторов и скаляров, будем пользоваться следующим правилом:
1. Если оператор  действует на какое-либо произведение, то в первую очередь учитывается его дифференциальный характер, а затем уже векторное свойство.
действует на какое-либо произведение, то в первую очередь учитывается его дифференциальный характер, а затем уже векторное свойство.
2. Чтобы отметить тот факт, что  не воздействует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом
не воздействует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом  или «стрелкой» (например
или «стрелкой» (например 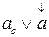 ), который в окончательном результате может быть снят.
), который в окончательном результате может быть снят.
3. Все величины, на которые оператор  не воздействует, в окончательном результате ставятся впереди
не воздействует, в окончательном результате ставятся впереди  , т.е. слева от него.
, т.е. слева от него.
Так, например, в 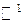 оператор
оператор  есть оператор дифференцирования
есть оператор дифференцирования
функции одной переменной и тогда правило нахождения производной произведения сводится:

ЗАМЕЧАНИЕ.
Под дифференциальными операциями II-го порядка понимаются операции, в которых символ  встречается дважды. При этом формулы векторной алгебры считаются справедливыми при замене обычного вектора символическим вектором
встречается дважды. При этом формулы векторной алгебры считаются справедливыми при замене обычного вектора символическим вектором  .
.
Усвоим некоторые элементы техники обращения с оператором  .
.
Вы можете проверить получающиеся формулы в координатах.
1) Пусть  , тогда
, тогда

2) 
3) 
= 
4) 

= 
Наряду с обозначениями векторного произведения 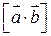 будем использовать и
будем использовать и  .
.
Нами будет использовано и двойное векторное произведение, известное вам из аналитической геометрии (1 семестр):

5) 
=  .
.
6) 
= 
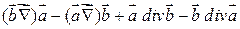 .
.
7)  .
.
Вектор  поэтому скалярное произведение равно 0, т.е.
поэтому скалярное произведение равно 0, т.е.  . Т.е. поле вихря вектора
. Т.е. поле вихря вектора  не имеет источников и стоков.
не имеет источников и стоков.
8)  .
.
Т.к. векторы  и
и  параллельны, т.е. поле вектора
параллельны, т.е. поле вектора  безвихревое.
безвихревое.
9)  .
.
10) Наряду с  используют оператор Лапласа или Лапласиан.
используют оператор Лапласа или Лапласиан.
Df. Оператором Лапласа или Лапласианом называется закон образования дивергенции от вектора  :
:
 физический смысл. Численное значение Лапласиана определяет плотность источников (если
физический смысл. Численное значение Лапласиана определяет плотность источников (если  ) или стоков (если
) или стоков (если  ) векторного поля
) векторного поля  .
.
Справедлива формула:
 , где символ
, где символ 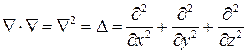 , так что
, так что 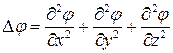 .
.
Df. Скалярное поле  , удовлетворяющее условию
, удовлетворяющее условию  , называется лапласовым или гармоническим полем.
, называется лапласовым или гармоническим полем.
Дифференциальные операции II -го порядка можно для наглядности записать в виде таблицы:
|
| Скалярное поле 
| Векторное поле | |

| 
| 
| |

| ---------------------------- | 
| ---------------------------------- |
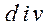
| 
| ----------------- | 
|
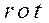
| 
| ----------------- | 
|
ТАБЛИЦА ОСНОВНЫХ ВЕЛИЧИН ПОЛЯ
| Наименование величины и обозначение | Определение или запись с помощью операторов Гамильтона и Лапласа | Формула записи в декартовых координатах |
| -1- | -2- | -3- |
Градиент скалярного поля 

| 
| 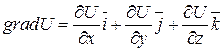
|
Расходимость векторного поля 
 ; ;
| 
| 
|
Поток векторного поля
 П
П
|
 ;
в частности через замкнутую поверхность S : ;
в частности через замкнутую поверхность S :
 (Теорема
Остроградского)
(Теорема
Остроградского)
| 
 
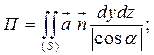

|
Ротор векторного поля

 ; ;
| 
|  +
+ 
|
| -1- | -2- | -3- |
Работа (линейный интеграл) векторного поля вдоль контура  ;
W ;
W
|  где
где

|  . .

 +
+ 
|
| Циркуляция векторного поля
вдоль контура l. Ц
|  . .
| 
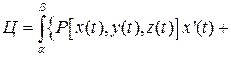
 +
+ +
+  . .
|

|  +
+  + +  . .
|
Дата добавления: 2020-11-15; просмотров: 235; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!


