Принцип математической индукции
Множество натуральных чисел
Натуральные числа - числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления), т.е натуральные числа - это естественные числа.
Всего существуют два подхода к пониманию натуральных чисел- это числа, используемые при:
1) перечислении (нумеровании) предметов (например:первый, второй, третий…и т.д.). Этот подход, общепринятый во многих странах мира (в том числе и в России);
2) обозначении количества предметов (например: нет предметов, один предмет, два предмета…и т.д.). Принят в трудах Бурбаки, где натуральные числа определяются как мощности конечных множеств.
Натуральными числами не являются: отрицательные и нецелые числа.
Множество всех натуральных чисел принято обозначать знаком N
Существует бесконечное множество натуральных чисел — для любого натурального числа найдётся другое натуральное число, большее его.
Аксиоматическое определение по Пеано
Определение 1. Пусть заданы множество  и отображение
и отображение  , удовлетворяющие условиям:
, удовлетворяющие условиям:
1. Область определения 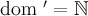 ,
,
2. Существует элемент 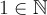 такой, что
такой, что  ,
,
3. Из 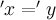 следует, что
следует, что  ,
,
4. Аксиома полной индукции: 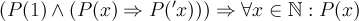 .
.
Тогда будем говорить, что  — натуральный ряд, а
— натуральный ряд, а  — множество натуральных чисел1).
— множество натуральных чисел1).
Пример 1. Реализацией натурального ряда может служить множество слов в алфавите из одной буквы с операцией дописывания буквы в конце слова.
Сложение в множестве натуральных чисел
|
|
|
Предложение 1. Для каждой пары натуральных чисел 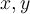 существует единственным образом определенное число, называемое суммой
существует единственным образом определенное число, называемое суммой  и
и  , обозначаемое через
, обозначаемое через 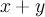 и удовлетворяющее условиям
и удовлетворяющее условиям
1. 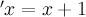 для всех
для всех  ,
,
2.  для всех
для всех  .
.
Предложение 2. Операция сложения 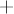 на множестве натуральных чисел обладает следующими свойствами:
на множестве натуральных чисел обладает следующими свойствами:
1. ассоциативность:  для любых натуральных
для любых натуральных 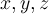 ;
;
2. коммутативность:  для любых натуральных
для любых натуральных 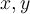 .
.
Умножение в множестве натуральных чисел
Предложение 3. Для каждой пары натуральных чисел 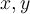 существует единственным образом определенное число, называемое произведением
существует единственным образом определенное число, называемое произведением  и
и  , обозначаемое через
, обозначаемое через  и удовлетворяющее условиям
и удовлетворяющее условиям
1.  для всех
для всех  ,
,
2.  для всех
для всех  .
.
Предложение 4. Операция умножения  на множестве натуральных чисел обладает следующими свойствами:
на множестве натуральных чисел обладает следующими свойствами:
1. ассоциативность: 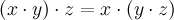 для любых натуральных
для любых натуральных 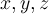 ;
;
2. коммутативность:  для любых натуральных
для любых натуральных 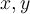 ;
;
3. дистрибутивность:  для любых натуральных
для любых натуральных 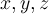 .
.
Реализация натуральных чисел как подмножества действительных
Пусть определено множество действительных чисел  2).
2).
Определение 2. Назовем множество 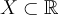 индуктивным3), если из того, что
индуктивным3), если из того, что  следует, что
следует, что  .
.
Определение 3. Множеством натуральных чисел  называется наименьшее индуктивное множество, содержащее 1.
называется наименьшее индуктивное множество, содержащее 1.
|
|
|
Предложение 5. Каждое натуральное число  можно представить как сумму конечного числа единиц 1.
можно представить как сумму конечного числа единиц 1.
Принцип математической индукции
Аксиома полной индукции 4) или индуктивность множества 5) позволяет применять
Принцип математической индукции. Предположим, что для каждого натурального  имеется некоторое утверждение
имеется некоторое утверждение 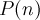 . Пусть утверждение
. Пусть утверждение 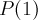 верно. Предположим также, что для каждого
верно. Предположим также, что для каждого  из истинности утверждения
из истинности утверждения 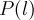 можно вывести истинность утверждения
можно вывести истинность утверждения  . Тогда утверждение
. Тогда утверждение 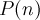 истинно для каждого натурального
истинно для каждого натурального 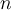 .
.
Пример 3. С помощью принципа математической индукции можно доказать истинность выражения  . Действительно, при
. Действительно, при  имеем верное выражение
имеем верное выражение 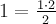 . Предположим, что верно выражение
. Предположим, что верно выражение  . Добавив к обеим частям равенства
. Добавив к обеим частям равенства  , получим
, получим
 , откуда следует истинность выражения
, откуда следует истинность выражения
 . Применив принцип математической индукции, получаем, что
. Применив принцип математической индукции, получаем, что  верно для любого натурального
верно для любого натурального 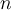 .
.
См. также
Дата добавления: 2020-11-15; просмотров: 67; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
