Обобщение алгоритма Брезенхема.
Лекции 5. Алгоритмы растрово-векторной графики.
 Растр и вектор.
Растр и вектор.
Основа растрового дисплея – растр – упорядоченная сетка пикселей. Каждое изображение непрерывно: фотография, рисунок и т.д., представляет собой множество точек, линий, сплошных областей. Т.к. растр – матрица дискретных элементов (пикселей), то любое непрерывное изображение нельзя абсолютно точно изобразить на растровом экране => необходима аппроксимация (приблизительное описание).
Растрирование (разложение в растр) – процесс определения пикселей, наилучшим образом аппроксимирующих непрерывное изображение. Процесс разложения в растр тесно связан с процессом визуализации изображения (растровая развертка).
Основными рассматриваемыми векторными примитивами являются:
Точка
Отрезок (прямая)
Дуга (эллипс, окружность)
Закраска замкнутой области (растровая развертка треугольника)
Текст (шрифты растровые и TT )
Алгоритмы вывода точки . Адрес в Буфере Кадра:
А=( Y * H + X )*РазмерЦвета [A]=C заносим цвет точки.
Алгоритмы развертки отрезков.
Главной задачей алгоритма развертки отрезков является вычисление координат пикселей, лежащих вблизи отрезков на двумерной растровой сетке. При решении этой задачи предполагают, что начальная и конечная точки отрезка имеют целочисленные координаты.
 Алгоритмы симметричны по X <-> Y от угла наклона прямой <45°
Алгоритмы симметричны по X <-> Y от угла наклона прямой <45°
|
|
|
Алгоритм проведения отрезка “ в лоб”.
 - уравнение прямой
- уравнение прямой
 ; [1]
; [1]  - tg угла наклона
- tg угла наклона
x: x1...x2 с шагом 1
y: рассчитывается y=Round( [1] )
При увеличении угла наклона появляются разрывы (Dx=1, Dy>1), т.е. при m<1 (угол < 45) используем [1], при m>1 (угол > 45), обратаная зависимость:
 [2]
[2]
y: y1...y2 с шагом 1
x: рассчитывается x=Round( [ 2 ] )
Недостатки: операции умножения, деления и дробная арифметика.
Данный алгоритм практически не используется.
Алгоритм Цифрового Дифференциального Анализатора.
 (const)
(const) 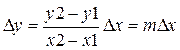 ;
; 
Dx и Dy для отрезка постоянны.
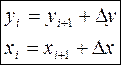 , где
, где 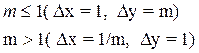
Xni = Round(Xi) Yni = Round(Yi)
Недостатки: работа с дробными числами. Данный алгоритм используется как основа для следующих алгоритмов растровой развертки.
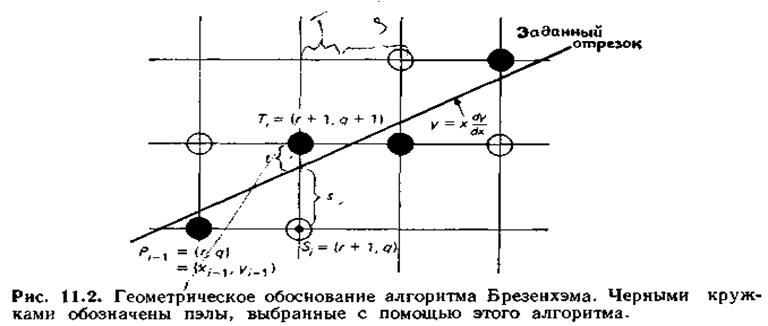
Целочисленный алгоритм Брезенхема.
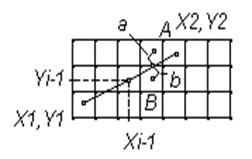 Вещественные переменные не используются совсем и, следовательно, округление не требуется.
Вещественные переменные не используются совсем и, следовательно, округление не требуется.
Оговорки:
m = (0..1); x2 > x1; (x1,y1) = (0,0); (x1,y1) ¹ (x2,y2)
Dx = 1 – всегда, Dy = { 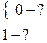


|

 - Определитель
- Определитель
Для упрощения вычислений вводят:

шаг  (от инкремент)
(от инкремент)
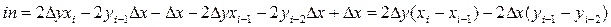
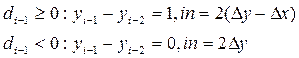
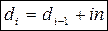 необходимо определить лишь одно значение d
необходимо определить лишь одно значение d
|
|
|
x1 = 0, y1 = 0; Dx = 1, x2 = 1
|
Обобщение алгоритма Брезенхема.
Были ограничения:
1. m < 1 (угол < 45); при m = 1..¥ - надо поменять x и y
2. x1=0, y1=0; смещение
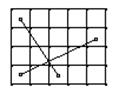
I квадрант:
x1=1, x2=5 Dx=4 “+”
y1=1, y2=3 Dy=2 “+”
(+1, +1v0) - приращение
II квадрант:
x1=3, x2=1 Dx=-2 “-”
y1=1, y2=4 Dy=3 “+”
 (-1, +1v0) - приращение
(-1, +1v0) - приращение
III квадрант:
x1=5, x2=1 Dx=-4 “-”
y1=3, y2=1 Dy=-2 “-”
(-1, -1v0) - приращение
IV квадрант:
x1=1, x2=3 Dx=2 “+”
y1=4, y2=1 Dy=-3 “-”
(+1, -1v0) - приращение
Sx = sign(x2-x1) = 
Sy= sign(y2-y1)
В алгоритме нужно заменить:
Inc(x) на 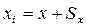
Inc(y) на 
Dx = x2 – x1 на Dx = |x2 – x1|
Dy = y2 – y1 на Dy = |y2 – y1|
Дата добавления: 2020-11-15; просмотров: 248; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
