Тригонометрическая и показательная форма комплексного числа
КОМПЛЕКСНЫЕ ЧИСЛА
Понятие комплексного числа
Числа вида a + bi , где a;b – действительные числа, число i определяется равенством i2 = - 1, называются КОМПЛЕКСНЫМИ числами.
Примеры: 3+2i; -7+I; 5-8i; -2-4i; ½ + (3/2)i и т.п.
i – мнимая единица. z - комплексное число.
z = a + bi –алгебраическая форма комплексного числа.
а – действительная часть комплексного числа(Re z)
b – мнимая часть комплексного числа(Im z).
0 = 0 + 0i – комплексный ноль
1 = 1 + 0i – действительная единица
i = 0 + i - мнимая единица
Представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве. Комплексное число – это двумерное число.
a + bi – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: z = bi + a или z = a + ib – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: z = a + bi
Комплексные числа изображаются на комплексной плоскости:

R -множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой C. Поэтому на чертеже следует поставить букву C, обозначая тот факт, что у нас комплексная плоскость.
Комплексная плоскость состоит из двух осей: Re z – действительная ось Im z – мнимая ось
Правила оформления чертежа такие же, как и для чертежа в декартовой системе координат. По осям нужно задать масштаб, отмечаем ноль, единицу 1 по действительной оси, единицу I по мнимой оси.
|
|
|
Построим на комплексной плоскости следующие комплексные числа:
 ,
,  ,
, 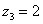
 ,
, 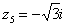 ,
, 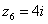
 ,
,  ,
,  ,
, 
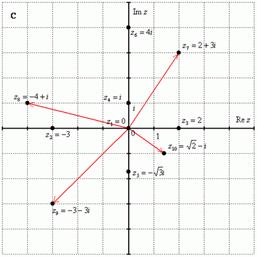
Алгебраическая форма комплексного числа.
Сложение, вычитание, умножение и деление комплексных чисел
z = a + bi - это алгебраическая форма записи комплексного числа.
Действия с комплексными числами в алгебраической форме основаны на алгебраических преобразованиях (приведение подобных слагаемых, группировка, вынесение за скобки общего множителя, раскрытие скобок и т.п.)
Рассмотрим два комплексных числа z1 = a1+ b1 i и z2 = a2+ b2 i
1. z1=z2 ↔ a1=a2 и b1=b2
2. z1+z2 = (a1+b1i) + (a2+b2i) = a1+b1i+a2+b2i = (a1+a2)+(b1+b2)i
3. z1-z2 = (a1+b1i) - (a2+b2i) = a1+b1i-a2-b2i = (a1-a2)+(b1-b2)i
4. z1∙z2 = (a1+b1i)( a2+b2i) = a1a2+a1b2i+b1ia2+b1b2i2= (a1a2-b1b2)+(a1b2+b1a2)i
| z1 | = | a1+b1i | = | (a1+b1i)( a2-b2i) |
| z2 | a2+b2i | (a2+b2i)( a2-b2i) |
5.
Примеры :
1). z1= 2 – 3i; z2=6+2i
z1 + z2 = 2 – 3i + 6 + 2i = 8 – i
z1 – z2 = 2 – 3i – 6 – 2i = - 4 – 5i
z1∙z2 = (2 – 3i)(6 + 2i) = 12 + 4i – 18i – 6i2 = 12 – 14i + 6 =18 – 14i
z 1 = 2 – 3i = (2 – 3i)(6 – 2i) = 12 – 4i – 18i + 6i2 = 12 – 22i – 6 = 6 – 22i =6– 22i
z2 6 + 2i (6 + 2i)(6 – 2i) 36 – 4i2 36 + 4 40 40 40
2). z1 =5 – i; z2= 1- i; z3= 3+2i
2z2 – z3= 2(1-i) – (3+2i) = 2 - 2i – 3 - 2i = -1 – 4i
5z1 + z2 = 5(5- i) + 1 – i = 25 – 5i + 1 – i = 26 – 6i
|
|
|
Выполнить самостоятельно :
z1 = 3 – 4i; z2 = 4 + i; z3 = - 2 + 3i;
Найти : z1 + 3z3; z2 – z3; 2z1 + 3z2; z1∙z2; z2∙z3; z2 : z1; (z1 + 3z3): z2
Решение квадратных уравнений.
Пример 1.
x2 + 1 = 0 ; x2 = - 1 = i2 ; x = ±√i2 = ±i ; x1 = -i;x2 = i
Пример 2.
x2 + 36 = 0; x2 = - 36 = 36i2; x = ±√36i2 = ±6i; x1 = - 6i;x2 = 6i;
Пример 3.
x2 + x + 2 = 0;
D = b2 – 4ac = 12 - 4∙1∙2 = - 7 = 7i2;
x1= (-b - √D):2a = (-1 - √7 i): 2 = -1/2 - √7/2 i;
x2= (-b + √D):2a = (-1 +√7 i):2 = -1/2 + √7/2
Выполнить самостоятельно :
Решить уравнение:
1). х2 + 4 = 0; 2). х2 + х + 3 = 0; 3). х2 – 2х + 5 = 0;
4). х2 – 7х + 20 = 0; 5). х2 + х + 7 = 0
Выполнить самостоятельно:
Вариант 1
1. Решить уравнение:
а). х2 + 25 = 0; б). х2 – 6х + 10 = 0; в). х2 + х + 1 = 0; г).х2 – 2х + 4 = 0
2. Вычислить:
[(z1 + 2z2)∙z3]:(z1∙z2), если z1 = 5 + i, z2 = -1 – i, z3 = 7 – i
Вариант 2
1. Решить уравнение:
а). х2 + 9 = 0; б). х2 – 2х + 6 = 0; в). х2 – 4х + 16 = 0; г). х2 – 3х + 5 = 0
2. Вычислить:
[(z1 + 2z2)∙z3]:(z1∙z2), если z1 = 3 + i; z2 = -2 + i ; z3 = 8 + i
Тригонометрическая и показательная форма комплексного числа
Любое комплексное число (кроме нуля)  можно записать в тригонометрической форме:
можно записать в тригонометрической форме:
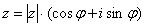 , где
, где 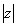 – это модуль комплексного числа, а
– это модуль комплексного числа, а 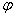 – аргумент комплексного числа. Изобразим на комплексной плоскости число
– аргумент комплексного числа. Изобразим на комплексной плоскости число  . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что
. Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что  :
:
|
|
|

Модулем комплексного числа  называется расстояние от начала координат до соответствующей точки комплексной плоскости. модуль – это длина радиус-вектора. Модуль комплексного числа
называется расстояние от начала координат до соответствующей точки комплексной плоскости. модуль – это длина радиус-вектора. Модуль комплексного числа  стандартно обозначают:
стандартно обозначают: 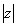 или
или  .По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа:
.По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа:  . Данная формула справедлива для любых значений «а» и «b».
. Данная формула справедлива для любых значений «а» и «b».
Примечание: модуль комплексного числа представляет собой обобщение понятия модуля действительного числа, как расстояния от точки до начала координат.
Аргументом комплексного числа  называется угол
называется угол 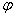 между положительной полуосью действительной оси
между положительной полуосью действительной оси 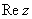 и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: 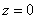 . Аргумент комплексного числа
. Аргумент комплексного числа  стандартно обозначают:
стандартно обозначают: 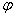 или
или  .
. 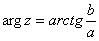
Модуль – длина (которая всегда неотрицательна), аргумент – угол.
Примеры:
1) Представим в тригонометрической форме число  . Найдем его модуль и аргумент. Очевидно, что
. Найдем его модуль и аргумент. Очевидно, что  . Формальный расчет по формуле:
. Формальный расчет по формуле: 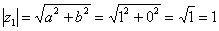 .
.
Очевидно, что 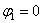 (число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:
(число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:  .
.
|
|
|
Обратное проверочное действие: 
2) Представим в тригонометрической форме число  . Найдем его модуль и аргумент. Очевидно, что
. Найдем его модуль и аргумент. Очевидно, что 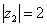 . Формальный расчет по формуле:
. Формальный расчет по формуле: 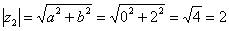 .
.
Очевидно, что 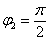 (или 90 градусов). Таким образом, число в тригонометрической форме:
(или 90 градусов). Таким образом, число в тригонометрической форме: 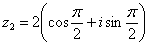 .
.
Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):

3) Представим в тригонометрической форме число  . Найдем его модуль и аргумент. Очевидно, что
. Найдем его модуль и аргумент. Очевидно, что  . Формальный расчет по формуле:
. Формальный расчет по формуле: 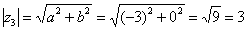 .
.
Очевидно, что  (или 180 градусов). Таким образом, число в тригонометрической форме:
(или 180 градусов). Таким образом, число в тригонометрической форме: 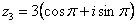 .
.
Проверка: 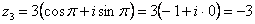
4) Представим в тригонометрической форме число 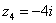 . Найдем его модуль и аргумент. Очевидно, что
. Найдем его модуль и аргумент. Очевидно, что  . Формальный расчет по формуле:
. Формальный расчет по формуле:  .
.
Аргумент можно записать двумя способами: Первый способ:  (270 градусов), и, соответственно:
(270 градусов), и, соответственно: 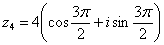 . Проверка:
. Проверка: 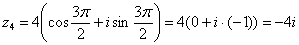
Однако более стандартно следующее правило: Если угол больше 180 градусов, то его записывают со знаком минус и противоположной ориентацией («прокруткой») угла:  (минус 90 градусов). Легко заметить, что
(минус 90 градусов). Легко заметить, что  и
и  – это один и тот же угол.
– это один и тот же угол.
Таким образом, запись принимает вид: 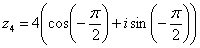
Формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число  . При этом возможны три варианта:
. При этом возможны три варианта:
1) Если  (1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле
(1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле 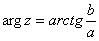 .
.
2) Если  (2-я координатная четверть), то аргумент нужно находить по формуле
(2-я координатная четверть), то аргумент нужно находить по формуле  .
.
3) Если  (3-я координатная четверть), то аргумент нужно находить по формуле
(3-я координатная четверть), то аргумент нужно находить по формуле  .
.
Пример:
Представить в тригонометрической форме комплексные числа: 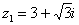 ,
, 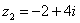 ,
, 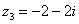 ,
, 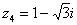 .
.

Представим в тригонометрической форме число 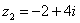 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.

Поскольку  (случай 2), то
(случай 2), то 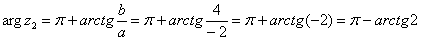
 – число
– число  в тригонометрической форме.
в тригонометрической форме.
Представим в тригонометрической форме число 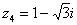 . Найдем его модуль и аргумент.
. Найдем его модуль и аргумент.
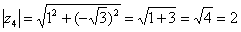
Поскольку  (случай 1), то
(случай 1), то 
Таким образом:
 – число
– число 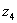 в тригонометрической форме.
в тригонометрической форме.
Числа 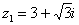 и
и 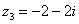 представьте в тригонометрической форме самостоятельно.
представьте в тригонометрической форме самостоятельно.
Дата добавления: 2020-11-15; просмотров: 93; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
