Векторное произведение двух векторов.
ЛЕКЦІЯ № 5.
Раздел 1. Линейная алгебра и аналитическая геометрия.
Тема: Векторы в системе координат.
Цели: расширить понятия о векторах, рассмотреть правила действий над векторами в системе координат, изучить формулу нахождения длины вектора.
План.
1. Действия над векторами, заданными своими координатами.
2. Длина вектора, расстояние между двумя точками на плоскости.
3. Деление отрезка в заданном соотношении.
Действия над векторами, заданными своими координатами.
С понятием вектора, как направленного отрезка, и векторных величин вы уже знакомы. Рассмотрим векторы в системе координат и действия над ними.
Пусть заданы векторы:
1) при сложении двух векторов их одноименные координаты складываются:
;
2) при вычитании двух векторов их одноименные координаты вычитаются:
;
3) при умножении вектора на число k , каждая координата вектора умножается на это число:
;
Например: даны векторы 
и 
. Найдем сумму, разность и произведение вектора на число 0,5:
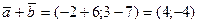
Длина вектора, расстояние между двумя точками на плоскости.
Если вектор задан своими координатами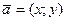 
, то его длина определяется по формуле:
Если вектор задан двумя точками 
и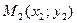 
то длину вектора 
определяют по формуле:
По этой формуле можно найти расстояние между двумя точками, так как длина вектора равна длине порождающего его отрезка.
Например, длина вектора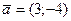 
равна:
|
|
|
.
Известно, что направление любого вектора 
определяется углами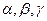 
, которые вектор образует с осями координат. Косинусы этих углов называются направляющими косинусами. Формулы для направляющих косинусов:
; 
; 
.
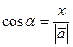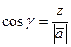Напомним определение коллинеарности векторов: векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат.
Деление отрезка в заданном соотношении.
Если отрезок АВ, координаты концов которого известны, точка С делит в заданном отношении 
, где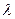 
- число, то координаты точки С можно найти по формуле:
; 
.
Если точка С делит отрезок АВ на две равные части, тогда координаты точки деления находим по формуле:
; 
.
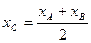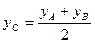Если есть две материальные точки и 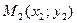, в которых сосредоточены массы 
и 
, то координаты точки центра масс этих двух материальных точек находится по формулам:
; 
.
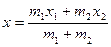Аналогично находятся координаты центра масс трех и более материальных точек.
Контрольные вопросы.
1. Что называется вектором и как найти координаты вектора?
2. Как вычислить длину вектора?
3. Какие векторы считаются равными?
|
|
|
4. Какие векторы называются коллинеарными?
5. Какие векторы называются ортогональными?
6. В чем заключается условие коллинеарности двух векторов?
7. Запишите формулы для нахождения координат центра масс трех материальных точек.
8. Какие действия можно выполнять над векторами?
Литература: В.П.Дубовик «Высшая математика», К.,2003, с50-53.
ЛЕКЦІЯ № 6
Раздел 1. Линейная алгебра и аналитическая геометрия.
Тема: Скалярное и векторное произведение векторов.
Цели: расширить понятия о векторах, рассмотреть правила скалярного и векторного умножения, изучить формулу нахождения угла между векторами.
План.
1. Скалярное произведения векторов.
2. Векторное произведение двух векторов.
3. Нахождение угла между векторами.
1. Скалярное произведения векторов.
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
.
Если хотя бы один из векторов равен нулю, то скалярное произведение равно нулю. Углом между векторами называется угол между их направлениями.
Рассмотрим, как находить скалярное произведение двух векторов в координатной форме.
Пусть два ненулевых вектора заданы своими координатами:
|
|
|
, .
Скалярным произведением двух векторов называется число, равное сумме произведений их одноименных координат:
.
Скалярное произведение обозначается одним из символов:
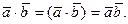
Если скалярное произведение двух векторов равно нулю, то эти векторы ортогональны.
Для скалярного произведения векторов имеет место переместительный, сочетательный и распределительный законы. Кроме того, скалярный квадрат вектора равен квадрату длины этого вектора: 
Векторное произведение двух векторов.
Векторным произведением векторов 
и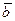 
называется вектор 
, который определяется тремя условиями:
1) длина вектора равна: 
;
2) вектор перпендикулярен каждому из векторов и ;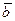
3) если 
, то векторы , , 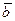образуют правую тройку векторов.
Векторное произведение обозначается одним из символов:
Рассмотрим алгебраические свойства векторного произведения:
1) От перестановки множителей векторное произведение меняет знак.
2) Скалярный множитель выносится за знак векторного произведения.
3) Выполняется дистрибутивный закон относительно сложения
Рассмотрим геометрические свойства векторного произведения:
4) Векторное произведение двух векторов равно нулю тогда и только тогда, когда эти векторы коллинеарные.
|
|
|
5) Модуль векторного произведения неколлинеарных векторов равен площади параллелограмма, построенного на векторах и 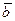, отнесенных к общему началу:
.
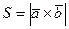Пусть векторы и 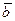заданы своими координатами в пространстве:
, 
,
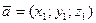тогда их векторное произведение можно определить по формуле:
.
Пример. Найти площадь параллелограмма, построенного на векторах 
и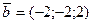 
.
Решение:
согласно свойства 5), имеем 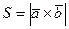, значит
Дата добавления: 2020-11-15; просмотров: 102; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!