Тест ранговой корреляции Спирмена
При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшатся с увеличением значения X. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений 
и значения 
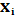будут коррелированы. Значения 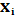и ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции: 
где d — разность между рангами значени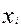й 
и 
.
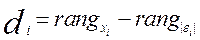Если соответствующий коэффициент корреляции для генеральной совокупности равен нулю, т. е. гетероскедастичность отсутствует, то коэффициент ранговой корреляции имеет нормальное распределение с математическим ожиданием 0 и дисперсией
.
Соответствующая тестовая статистика равна:
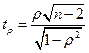
Следовательно, если значение тестовой статистики, вычисленное по вышеприведенной формуле, превышает при выбранном уровне значимости определяемое по таблице критических точек распределения Стьюдента, то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции, а следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.
Тест Голдфелда – Квандта
В данном случае предполагается, что стандартное отклонение 
пропорционально значению 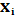переменной X в этом наблюдении. Предполагается, что имеет нормальное распределение и отсутствует автокорреляция остатков.
Тест Голдфелда – Квандта состоит в следующем:
|
|
|
1. Все n наблюдений упорядочиваются по величине X по возрастающей.
2. Вся упорядоченная выборка после этого разбивается на две подвыборки размерностей k и k соответственно, средние (N – 2k) элементов исходного ряда отбрасываются.
3. Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для второй подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям X верно, то дисперсия регрессии (сумма квадратов остатков RSS1 ) по первой подвыборке будет существенно меньше дисперсии регрессии (суммы квадратов остатков RSS2 ) по второй подвыборке.
4. Для сравнения соответствующих дисперсий строится следующая F-статистика: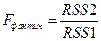 
Находим табличное значение F для df=(k – m – 1)
Здесь (k – m – 1) – число степеней свободы соответствующих выборочных дисперсий (m – количество объясняющих переменных в уравнении регрессии).
5. Если 
, то гипотеза об отсутствии гетероскедастичности отклоняется.
6. Если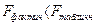 
, то гипотеза об отсутствии гетероскедастичности принимается.
Естественным является вопрос, какими должны быть размеры подвыборок для принятия обоснованных решений. Для парной регрессии Голдфелд и Квандт предлагают следующие пропорции: n = 30, k = 11; n = 60, k = 22.
|
|
|
Этот же тест может быть использован при предположении об обратной пропорциональности между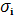 
и значениями объясняющей переменной. При этом F-статистика примет вид: 
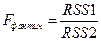(если X убывает).
Тест Глейзера
Тест Глейзера предполагает анализ зависимостей между дисперсиями отклонений 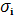и значениями переменной :
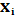В качестве зависимой переменной для изучения гетероскедастичности выбирается абсолютная величина остатков, т. е. осуществляется регрессия
где 
– случайный член.
В качестве функций f обычно выбираются функции вида 
, где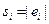 
- оценка .
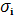Регрессия осуществляется при разных значениях γ, затем выбирается то значение, при котором коэффициент β оказывается наиболее значимым, т. е. имеет наибольшее значение t-статистики. Изменяя значения γ, можно построить различные регрессии. Обычно γ = …, -1, -0.5, 0, 0.5, 1, 1.5, … . Статистическая значимость коэффициента β в каждом конкретном случае фактически означает наличие гетероскедастичности. Если для нескольких регрессий коэффициент β оказывается статистически значимым, то при определении характера зависимости обычно ориентируются на лучшую из них оценивая коэффициент детерминации и статистическую значимость коэффициента β.
|
|
|
Дата добавления: 2020-11-15; просмотров: 100; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!