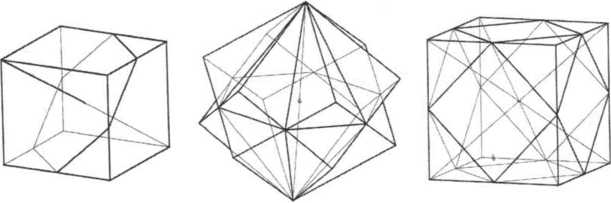
Многогранники в 1700-2000 годах
В 1700-2000 годы главным стимулом интереса к многогранникам стало не искусство, а математика. Вначале Рене Декарт (1596—1650) доказал, что сумма угловых дефектов при вершинах многогранника (разностей между 360° и суммой углов между ребрами каждой грани, сходящейся в рассматриваемой вершине) для всех выпуклых многогранников одинакова и равна 720°.
Следующая формула, сыгравшая огромную роль при изучении многогранников, была открыта великим Леонардом Эйлером (1707—1783). Знаменитая формула Эйлера Г + В = Р + 2 (сумма числа граней и вершин равна числу ребер, увеличенному на 2) удивительным образом выполняется для всех выпуклых многогранников. Она позволила подойти к изучению многогранников с новой стороны.
Создатель начертательной геометрии Гаспар Монж (1746—1818), подобно художникам Возрождения, использовал многогранники в качестве идеальных моделей при работе над своей теорией. Луи Пуансо (1777—1859) описал еще два звездчатых многогранника, получаемых из описанных Кеплером, пополнив коллекцию правильных невыпуклых многогранников, а Огюстен Луи Коши (1789—1857) доказал, что эти четыре многогранника Кеплера — Пуансо являются единственно возможными. Эжен Шарль Каталан (1814—1894) исследовал многогранники, двойственные архимедовым телам и с их помощью открыл так называемые каталановы тела.
Ронделе опубликовал развертки правильных многогранников на плоскости (1812), Жозеф Бертран в 1848 году описал различные группы звездчатых многогранников, а великий французский математик Анри Пуанкаре (1854—1912) получил новые доказательства и обобщения для формулы Эйлера, открыв новые подходы к изучению многогранников в целом.
|
|
|
Макс Брюкнер (1860—1934) в 1900 году создал рисунки и фотографии своей коллекции из 146 бумажных моделей многогранников. Полную классификацию 92 выпуклых неоднородных многогранников с правильными гранями составил Норман Джонсон в 1966 году, а Виктор Залгаллер в 1969 году показал, что этот список является полным и окончательным.
Многогранники в наши дни
В начале нынешнего столетия математические исследования продолжаются, подробно изучаются новые семейства многогранников.
Однако новый импульс изучению многогранников дала компьютерная графика и вычислительная геометрия. Благодаря своей геометрической простоте многогранники прекрасно подходят для тестирования программ для работы с трехмерной графикой. В Интернете существует множество страниц, посвященных многогранникам.
Большие семейства многогранников
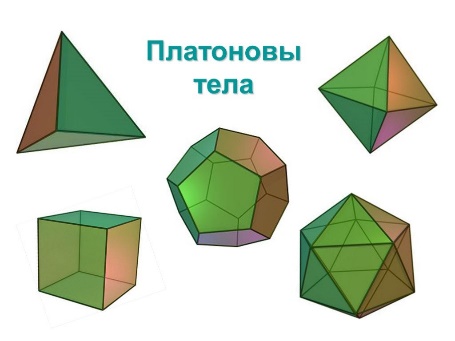Пять Платоновых тел
Правильный многогранник – это выпуклый многогранник, такой, что все его грани являются равными правильными многоугольниками, и в каждой вершине сходятся одинаковое число ребер.
|
|
|
В следующей таблице приведены основные данные об этих телах
| Тетраэдр | Куб | Октаэдр | Додекаэдр | Икосаэдр | |
| Число граней | 4 треугольника | 6 квадратов | 8 треугольников | 12 пятиугольников | 20 треугольников |
| Число вершин | 4 | 8 | 6 | 20 | 12 |
| Число ребер | 6 | 12 | 12 | 30 | 30 |
| Двугранный угол | 70º32' | 90º | 109º28' | 116º34' | 138º11' |
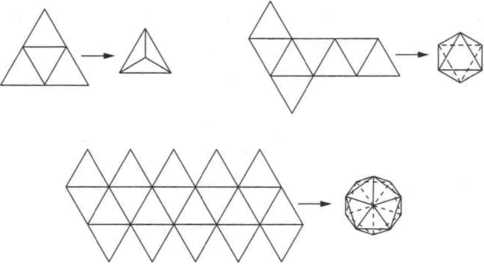Платоновы тела можно изготовить из бумаги. Для этого существуют развертки – схематичное изображение многогранников на бумаге. Эти развертки идеально подходят для изготовления бумажных моделей. Тетраэдры, октаэдры и икосаэдры также можно изготовить из палочек и веревок — полученные модели будут устойчивыми, так как их грани имеют форму треугольников. Однако для кубов и додекаэдров вам потребуется добавить дополнительные диагонали, чтобы придать конструкции жесткость.
Почему правильных многогранников всего пять? Существуют ли другие правильные многогранники? Ответ на этот вопрос отрицательный, и причина этому очень проста. Если т правильных п-угольников должны сходиться в одной вершине (и при этом не располагаться в одной плоскости), то, поскольку углы этих многоугольников будут равны 180° — 360°/п = 180° n — 2)/n, должно выполняться неравенство т • 180° (n — 2)/n < 360°, откуда имеем неравенство (т — 2) (n — 2) < 4. Его возможные решения представлены в таблице
|
|
|
| M | n | Фигура |
| 3 | 3 | Тетраэдр |
| 3 | 4 | Куб |
| 4 | 3 | Октаэдр |
| 3 | 5 | Додекаэдр |
| 5 | 3 | Икосаэдр |
Таким образом, подходящими многоугольниками являются только равносторонний треугольник, квадрат и правильный пятиугольник, откуда следует, что существует всего пять правильных многогранников. Теперь, когда мы рассмотрели это семейство многогранников в целом, мы можем выделить особые черты каждого из них.
Тетраэдр
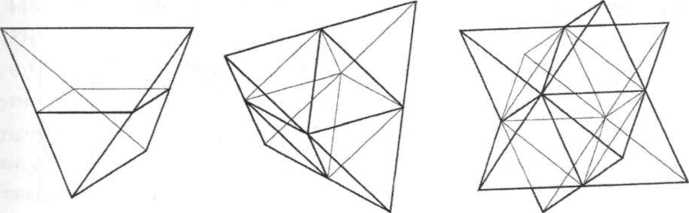Это прекрасный многогранник, противоположные ребра которого скрещиваются в пространстве перпендикулярно друг другу (под углом 90°). Его геометрический центр находится на пересечении четырех его высот (прямых, соединяющих вершины с центрами противолежащих граней) и отстоит от оснований высот на расстояние, равное четверти высоты. В то же время геометрический центр тетраэдра — это середина отрезков, соединяющих середины двух противоположных ребер.
На рисунке вы также можете видеть одно интересное сечение тетраэдра, которое имеет форму квадрата, так как является частью октаэдра, расположенного внутри тетраэдра. Кроме того, на иллюстрации показано, как из двух тетраэдров рождается прекрасный невыпуклый многогранник, центральной частью которого является октаэдр.
|
|
|
Куб
Длины диагонали граней куба единичной стороны равны √2, длина главной диагонали — √3. Среди сечений куба выделяются равносторонние треугольники и удивительный правильный шестиугольник, делящий куб на две равные части.
|
|
На рисунке представлен невыпуклый многогранник, состоящий из кубов, имеющих общее шестиугольное сечение. Вы также можете видеть, как различные шестиугольные сечения куба определяют новый многогранник — кубооктаэдр.
Октаэдр
Октаэдр можно представить как две правильные четырехугольные пирамиды, соединенные основаниями (то есть как бипирамиду), либо как два треугольника, распложенных параллельно (повернутых на пол-оборота), между которыми вставлены треугольные грани (то есть как антипризму).
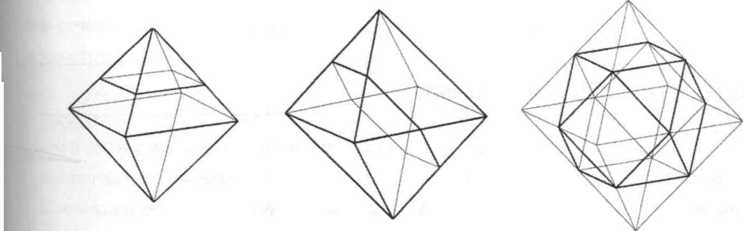
Если соединить середины верно выбранных шести ребер октаэдра, то есть если иссечь его плоскостью, параллельной двум параллельным граням, то мы получим любопытное шестиугольное сечение. Если мы рассмотрим четыре шестиугольных сечения, то получим новый многогранник с квадратными и треугольными гранями внутри октаэдра (кубооктаэдр).
Додекаэдр
Додекаэдр можно получить совмещением двенадцати правильных пятиугольников (следовательно, его размеры будут также соответствовать золотому сечению) или представить его в виде куба, дополненного шестью «крышами» — частями пятиугольников.
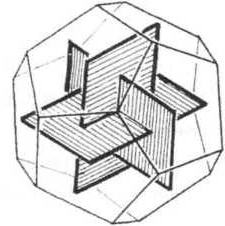
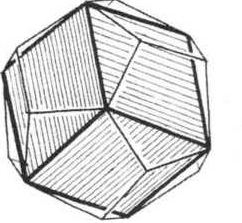
Связь додекаэдра с кубом и икосаэдром.
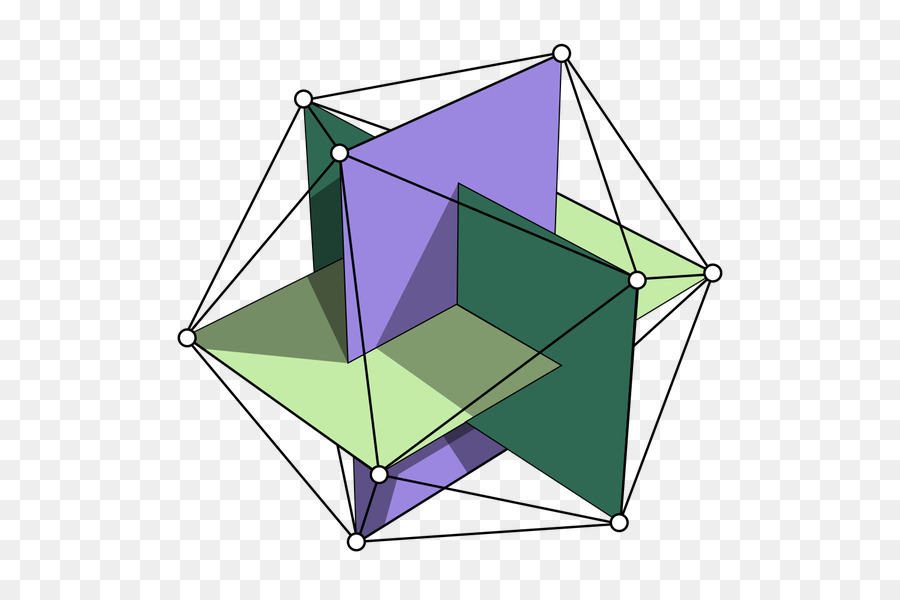Икосаэдр
На следующем рисунке три прямоугольника золотого сечения помещены внутри икосаэдра. Благодаря этому несложно выразить координаты его вершин. Двенадцать вершин трех равных прямоугольников, расположенных так, как показано на рисунке, определяют выпуклый многогранник с треугольными гранями. Любопытно, что его грани будут равносторонними треугольниками только тогда, когда эти прямоугольники будут прямоугольниками золотого сечения.
Пирамиды и бипирамиды
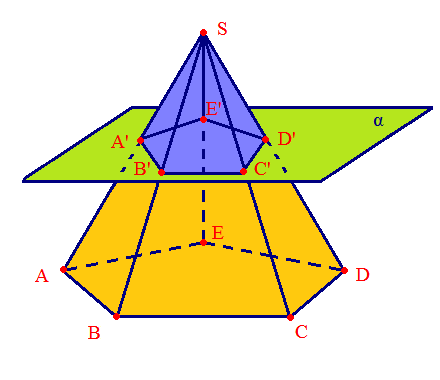Пирамиды, построенные египтянами и майя, — это выпуклые многогранники, образованные выпуклыми многоугольниками, лежащими в основании, и отрезками, соединяющими точку, не лежащую на плоскости основания, с его вершинами. Единственная пирамида, которая является правильным многогранником, — это знаменитый правильный тетраэдр (все его грани — равные между собой равносторонние треугольники). Если исключить условие равенства граней, но сохранить требование, чтобы все грани пирамиды были правильными многоугольниками, мы получим пирамиду с квадратным основанием и боковыми гранями в виде равносторонних треугольников и пирамиду с пятиугольным основанием и боковыми гранями в виде равносторонних треугольников. Если вершина пирамиды смещена в пространстве, такая пирамида называется неправильной. Если соединить две пирамиды основаниями, образуется бипирамида. Например, бипирамидой является правильный октаэдр. Объем произвольной пирамиды равен одной трети произведения площади ее основания на высоту. В качестве приближения пирамиды можно использовать конус. При сечении пирамиды, например, плоскостью, параллельной ее основанию, образуются две фигуры: новая пирамида и усеченная пирамида.
Призмы и антипризмы
Если поднять многоугольник над плоскостью, на которой он изображен, перпендикулярно ей, то образуется прямая призма, которая определяется двумя параллельными основаниями — равными многоугольниками и боковыми прямоугольными гранями. Объем подобных фигур вычисляется как произведение площади основания на высоту.
Если основания призмы смещены относительно друг друга, призма называется наклонной. Если соединить центры тяжести граней призмы, получится бипирамида, которая будет двойственной призме. Антипризмы, которые также называются призматоидами, возникают при рассмотрении двух параллельных граней, которые являются равными выпуклыми многоугольниками, при этом верхняя грань повернута относительно нижней, а каждая вершина верхней грани соединена с двумя соответствующими вершинами нижней грани. Таким образом получается фигура, основаниями которой являются равные многоугольники, повернутые относительно друг друга, а боковые грани имеют форму треугольников. Основаниями правильных антипризм являются правильные n-угольники, а боковыми гранями — равносторонние треугольники. С увеличением п антипризмы будут становиться все ниже и ниже. Какой же многогранник является первой антипризмой? При п = 3 мы получим... октаэдр!
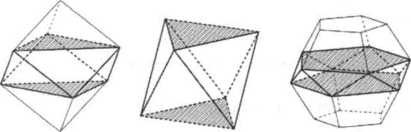Октаэдр — это единственная антипризма и правильный многогранник одновременно. В мире антипризм нас поджидает большой сюрприз: всякий правильный многогранник является либо пирамидой, либо антипризмой, либо объединением антипризмы и нескольких пирамид (усеченных пирамид).
Дельтаэдры
Дельтаэдры — это выпуклые многогранники, грани которых — равные между со6ой равносторонние треугольники. Название взято от греческой заглавной буквы дельта, которая имеет форму равностороннего треугольника. Существует бесконечно много дельтаэдров, но из них только восемь выпуклы, и они имеют 4, 6, 8, 10, 12, 14, 16 и 20 граней.
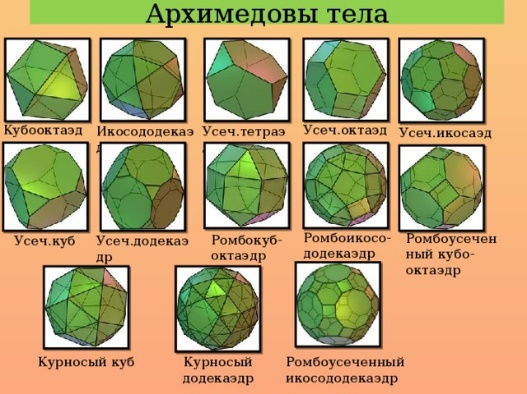Архимедовы тела
Согласно «Математическому собранию» Паппа Александрийского (середина XVI века), Архимед создал трактат о 13 полуправильных (архимедовых) многогранниках. Полуправильные многогранники — это выпуклые многогранники (они не являются ни призмами, ни антипризмами), гранями которых выступают равные правильные многоугольники двух или трех видов, а в каждой вершине сходится одинаковое число ребер.
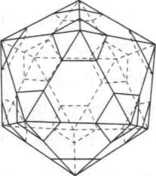
Особый интерес представляют два случая. Многогранник Кельвина, гранями которого являются шестиугольники и квадраты, образуется простым усечением правильного октаэдра, при этом линии среза делят его ребра на три равные части. Этот многогранник — единственное архимедово тело, при повторении которого можно заполнить пространство целиком.
Каталановы тела
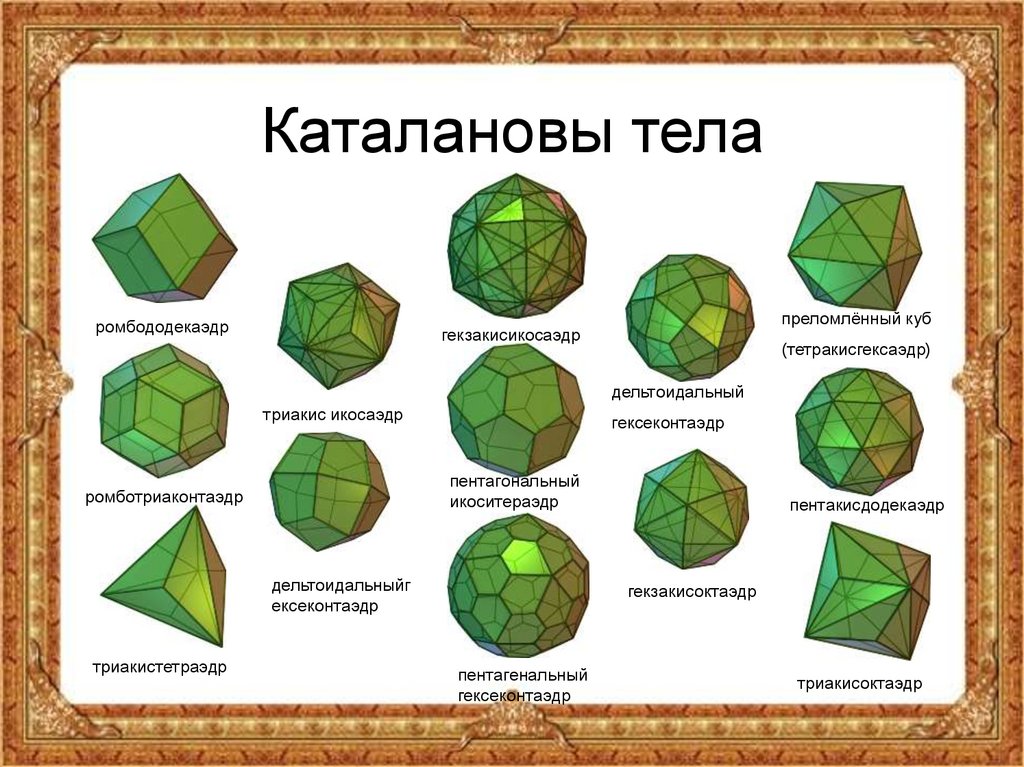Эжен Шарль Каталан (1814—1894) был выдающимся бельгийским математиком, именем которого назван важный класс чисел и примечательная группа многогранников. Каталановы тела — это 13 многогранников, двойственных архимедовым телам, то есть многогранники получаемые на 13 архимедовых тел. В то время как многогранники, двойственные
пяти правильным многогранникам, принадлежат к тому же семейству, архимедовы тела порождают 13 совершенно новых многогранников. Как не раз случалось в истории, до конца XIX века никто не уделял внимания этим объектам.
Грани каталановых тел не являются правильными многоугольниками. Число вершин каталанова тела совпадает с числом граней соответствующего ему архимедова тела, а число граней — с числом вершин архимедова тела. Любопытно, что в любое каталаново тело можно вписать сферу, которая будет касаться всех его граней, в то время как для архимедовых тел можно провести описанные сферы, которые будут проходить через все их вершины.
Звезчатые многогранники
Некоторые звездчатые многоугольники, например пентаграмма и звезда Давида в древности имели мистическое значение. Пентаграмма образуется при проведении всех диагоналей правильного пятиугольника или при продолжении его сторон до пересечения. Звезда Давида строится продолжением сторон правильного шестиугольника или вложением двух равносторонних треугольников, повернутых относительно друг друга.
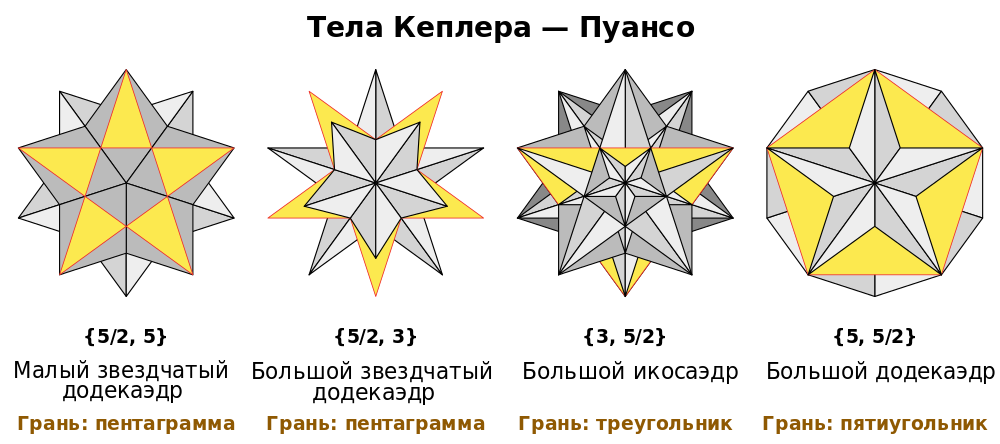
Первыми звездчатые многоугольники изучили Томас Брадвардин (1290—1349). Шарль де Бовель (1479 — ок. 1566) и Иоганн Кеплер (1571—1630), последний из которых попытался описать звездчатые многогранники. Он использовал два способа их построения: путем продолжения ребер и путем расширения граней исходных многогранников. Кеплер открыл первую пару звездчатых многогранников, полученных расширением додекаэдра и икосаэдра, и отметил, что на основе остальных трех правильных многогранников построить звездчатые многогранники невозможно. Луи Пуансо, ничего не зная о звездчатых многогранниках Кеплера, начал скрупулезный и подробный анализ всех звездчатых многогранников, комбинируя как обычные, так и звездчатые многоугольники, ребра которых пересекаются в точках, не являющихся вершинами (пентаграмма, звезда Давида и другие). В результате Пуансо не только повторно открыл два многогранника Кеплера, но и обнаружил два новых: большой додекаэдр и большой икосаэдр.
Сам Пуансо предположил, что описанные им четыре звездчатых многогранника, вероятно, являются единственно возможными правильными многогранниками такого типа. Лишь в 1812 году Огюстен Луи Коши смог привести убедительное доказательство гипотезы Пуансо. Четыре многогранника, которые сегодня носят имя Кеплера — Пуансо, являются единственно возможными правильными звездчатыми многогранниками.
Дата добавления: 2020-04-25; просмотров: 564; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!