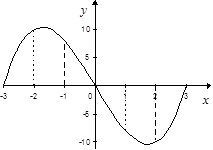Непрерывная функция задана на закрытом промежутке (отрезке).
|
|
Рассмотрим для примера график функции 
. На промежутке 
наибольшее значение функции достигается на левом конце промежутка при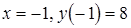 
; наименьшее – в точке минимума при 
.
Если взять промежуток 
, то наибольшее значение достигается в точке максимума при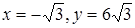 
, а наименьшее – на правом конце промежутка при 
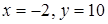. На промежутке 
наибольшее значение функции на левом конце при 
, наименьшее – на правом при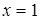 
.
Следовательно, в зависимости от выбранного промежутка изменения переменной x наибольшее или наименьшее значение непрерывной функции может достигаться или на концах промежутка, или в точках экстремума.
Итак, чтобы найти наибольшее или наименьшее значение непрерывной функции на отрезке, нужно найти производную функции и определить ее критические точки. Затем вычислить значения функции на концах промежутка и в тех критических точках, которые попадают на промежуток. Из полученных значений выбрать наибольшее и наименьшее значение.
Функция задана на открытом промежутке
Если непрерывная функция задана на открытом промежутке, то на этом промежутке она может не иметь либо наибольшего, либо наименьшего значений, либо ни того, ни другого. Для решения задачи необходимо провести исследование функции на монотонность или выяснить поведение функции вблизи концевых точек.
Пусть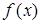 
задана на 
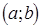. Если на всем этом промежутке она монотонно возрастает или убывает, у нее нет ни наибольшего, ни наименьшего значения.
|
|
|
Если внутри 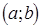имеется точка 
единственного экстремума функции, тогда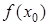 
– наименьшее значение функции, если этот экстремум является минимумом и 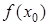– наибольшее значение функции, если этот экстремум является максимумом.
Если внутри 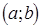имеется несколько экстремумов, то задачу можно решить с помощью построения графика.
Определение промежутков выпуклости и вогнутости
Функция называется выпуклой (выпуклой вверх) на данном промежутке, если ее график лежит не выше (ниже или касается) касательной, проведенной в любой точке этого промежутка (рис. 5).
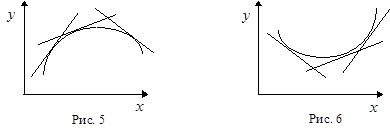
Функция называется вогнутой (выпуклой вниз) на данном промежутке, если ее график лежит не ниже (выше или касается) касательной, проведенной в любой точке этого промежутка (рис. 6).
Примечание: наличие касательной предполагает, что функция является дифференцируемой на промежутке.
На рис. 5 видно, что на участке выпуклости функция вначале возрастает, затем убывает, т.е. первая производная меняет знак с “+” на “–”, другими словами, убывает. Следовательно, вторая производная 
(производная от 
) отрицательна (см. п. 1.1.). Аналогично, из рис. 6 видно, что на участке вогнутости функция вначале убывает, затем возрастает, т.е. первая производная меняет знак с “–”на “+”, возрастает и, следовательно, (производная от ) положительна.
|
|
|
Чтобы определить промежутки выпуклости и вогнутости функции, нужно найти ее вторую производную , определить критические точки второй производной, т.е. точки, в которых она равна нулю или не существует. Затем определить знак второй производной в промежутках между критическими точками и в соответствии со знаком определить промежутки выпуклости и вогнутости.
Дата добавления: 2020-04-25; просмотров: 77; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!