Задания для самостоятельной работы
1. Исследовать на экстремум функции
а) 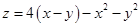 ; б)
; б) 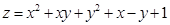
3. Убедиться, что функция 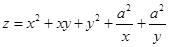 имеет минимум в точке
имеет минимум в точке 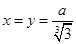 .
.
4. Убедиться, что при 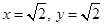 и при
и при 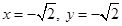 функция
функция 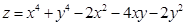 имеет минимум.
имеет минимум.
5. Убедиться, что при  функция
функция 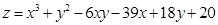 имеет минимум.
имеет минимум.
6. Найти стационарные точки функции 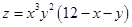 , удовлетворяющие условию
, удовлетворяющие условию  , и исследовать их характер.
, и исследовать их характер.
Наибольшее и наименьшее значение функции
Пусть функция 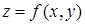 непрерывна в некоторой замкнутой области. Тогда в силу второй теоремы Вейерштрасса функция достигает в этой области своего наибольшего и наименьшего значения. Это может происходить во внутренней точке
непрерывна в некоторой замкнутой области. Тогда в силу второй теоремы Вейерштрасса функция достигает в этой области своего наибольшего и наименьшего значения. Это может происходить во внутренней точке 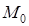 , тогда для дифференцируемой функции
, тогда для дифференцируемой функции 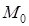 – стационарная точка, которую находим с помощью необходимых условий экстремума. Если же своего наибольшего (наименьшего) значения функция достигает на границе области, то выражают, например, переменную
– стационарная точка, которую находим с помощью необходимых условий экстремума. Если же своего наибольшего (наименьшего) значения функция достигает на границе области, то выражают, например, переменную 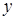 из уравнения границы, подставляют в
из уравнения границы, подставляют в 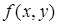 и исследуют на экстремум полученную функцию одной переменной. Остаётся подсчитать значение функции во всех полученных точках и выбрать среди них наибольшее и наименьшее. Заметим, что при этом не надо проводить дополнительные исследования с помощью достаточного условия экстремума.
и исследуют на экстремум полученную функцию одной переменной. Остаётся подсчитать значение функции во всех полученных точках и выбрать среди них наибольшее и наименьшее. Заметим, что при этом не надо проводить дополнительные исследования с помощью достаточного условия экстремума.
Пример 1. В области 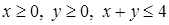 найти наибольшее и наименьшее значение функции
найти наибольшее и наименьшее значение функции 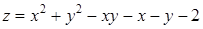 .
.
Решение . Функция непрерывна и дифференцируема на всей плоскости.
1. Приравняем нулю частные производные:
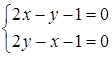
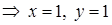 .
. 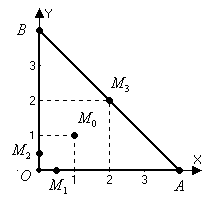
Получили единственную стационарную точку 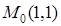 , лежащую внутри заданной области. Значит, если функция
, лежащую внутри заданной области. Значит, если функция 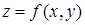 внутри области имеет экстремум, то это возможно только в точке
внутри области имеет экстремум, то это возможно только в точке 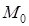 . Подсчитаем
. Подсчитаем 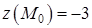 .
.
|
|
|
2. Исследуем поведение функции на границе области.
а) На стороне 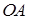 :
: 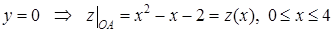 .
.
Функция 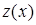 непрерывна на
непрерывна на  , следовательно, достигает на этом промежутке наибольшего и наименьшего значения. Находим стационарную точку из условия
, следовательно, достигает на этом промежутке наибольшего и наименьшего значения. Находим стационарную точку из условия 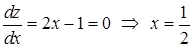 . Значит, если функция
. Значит, если функция 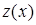 внутри промежутка
внутри промежутка 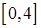 имеет экстремум, то это возможно только при
имеет экстремум, то это возможно только при 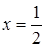 . Этому значению на стороне
. Этому значению на стороне 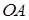 соответствует точка
соответствует точка 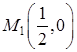 . Подсчитаем
. Подсчитаем 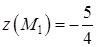 . Осталось найти значения функции
. Осталось найти значения функции 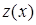 на концах промежутка
на концах промежутка  :
:  . Это соответствует значениям функции
. Это соответствует значениям функции 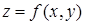 в углах
в углах 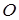 и
и 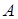 :
: 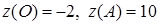
б) На стороне 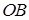 :
: 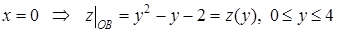 .
.
Находим на 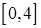 стационарную точку из условия
стационарную точку из условия 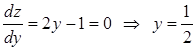 . Этому значению на стороне
. Этому значению на стороне 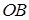 соответствует точка
соответствует точка 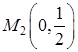 . Подсчитаем
. Подсчитаем 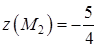 . Осталось найти значения функции
. Осталось найти значения функции  на конце
на конце 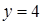 ::
:: 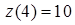 . Это соответствует значению функции
. Это соответствует значению функции 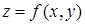 в углу
в углу 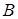 :
: 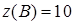 .
.
в) На стороне 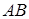 :
: 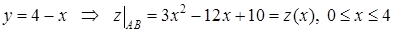 .
.
Находим на 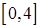 стационарную точку:
стационарную точку:  . Этому значению на стороне
. Этому значению на стороне 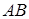 соответствует точка
соответствует точка 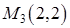 . Подсчитаем
. Подсчитаем 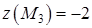 . Значения функции в углах
. Значения функции в углах 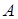 и
и 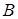 уже найдены.
уже найдены.
3. Выпишем значения функции в стационарных точках:
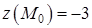 ,
, 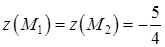 ,
, 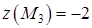
и значения функции в углах:
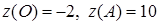
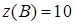 .
.
Среди этих значений выбираем наибольшее и наименьшее:
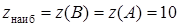 ,
, 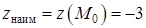 .☻
.☻
|
|
|
Задания для самостоятельной работы
1.Найти наибольшее и наименьшее значение функции 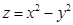 в круге
в круге 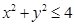 .
.
2. Найти наибольшее и наименьшее значение функции 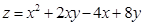 в прямоугольнике, ограниченном прямыми
в прямоугольнике, ограниченном прямыми 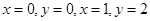
Дата добавления: 2020-04-25; просмотров: 92; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
