Связь координатного и естественного
Способов задания движения точки
Рассматривается прямолинейное движение точки при естественном и координатном способах задания движения точки (рис. 2.15).
Согласно рис. 2.15 уравнения прямолинейного равнопеременного движения при естественном и координатном способах задания движения точки по существу не отличаются друг от друга.
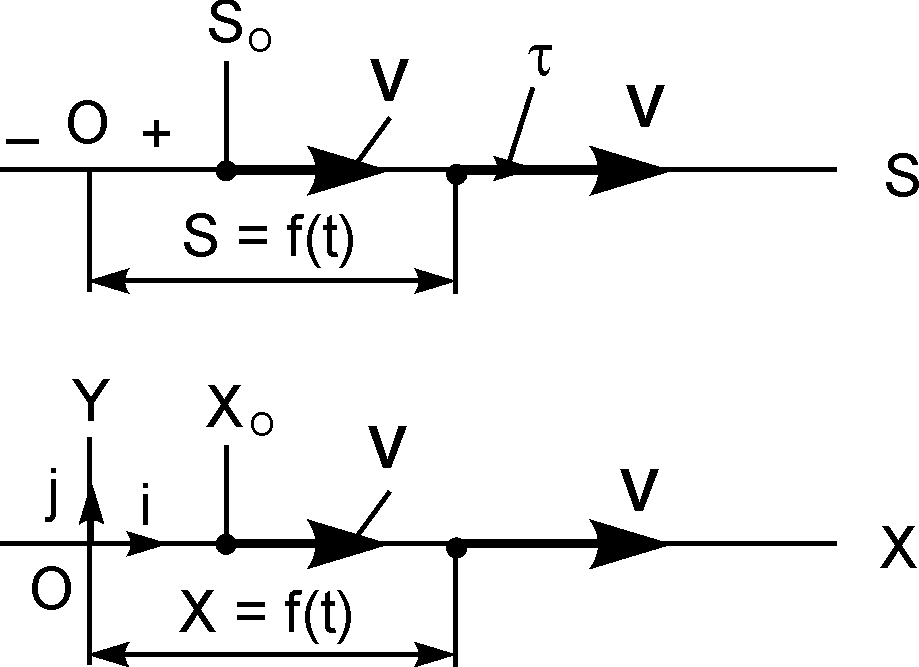 Рис. 2.15
Рис. 2.15
|
Естественный способ задания движения точки:
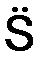 = const ≠ 0;
= const ≠ 0;
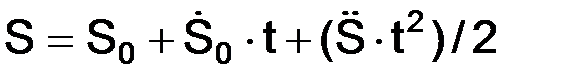 .
.
Координатный способ задания движения точки:
 = const ≠ 0;
= const ≠ 0;
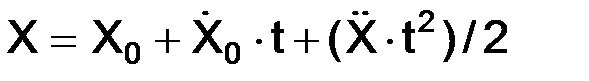 .
.
Таким образом, при прямолинейном равнопеременном движении точки уравнения X = f(t), S = f(t) в координатном и естественном способах задания имеют один и тот же вид.
Векторный способ задания движения точки
Положение точки в пространстве однозначно определяется заданием радиус-вектора r, проведённого из некоторого неподвижного центра О в данную точку М (рис. 2.16).
Для определения движения точки нужно знать, как изменяется с течением времени радиус-вектор, т. е. должна быть задана вектор-функция rаргумента t.
r = r(t).
Это выражение называют уравнением движенияпривекторном способе задания движения точки.
 Рис. 2.16
Рис. 2.16
|
Траектория движения точки является геометрическим местом концов радиус-вектора r. Иногда траекторию движения точки называют годографомрадиус-вектора r.
Векторный способ задания движения точки, как правило, используется при доказательстве теорем, так как он упрощает многие выводы и иногда подчёркивает физическую сущность явления.
|
|
|
Вектор V скорости точки направлен по касательной к траектории в сторону движения точки. Вектор скорости точки в данный момент равен производной от радиус-вектора точки по времени:
V = dr/dt=  ,
,
где (·) – символ однократного дифференцирования функции r = r(t) по времени.
Ускорение анаправлено в сторону вогнутости траектории движения точки. Вектор ускорения точки в данный момент времени равен первой производной от скорости Vили второй производной от радиус-вектора r = r( t ) точки по времени:
a = dV/dt = d2r/dt2= 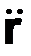 ,
,
где (··) – символ двойного дифференцирования функции r = r(t) по времени.
Если поместить начало неподвижной системы отсчёта OXYZ в точку О (точка О – полюс радиус-вектора r = r(t)), то можно связать координатный и векторный способы задания движения точки. Так как единичные векторы I, j, k системы отсчёта OXYZ постоянны, то справедливы следующие равенства:
r = i·X + j·Y + k·Z;
V =  = i·
= i·  + j·
+ j·  + k·
+ k· 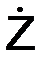 ;
;
a= 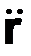 = i·
= i·  + j·
+ j·  + k·
+ k· 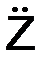 .
.
Варианты курсового задания К 1
«Определение скорости и ускорения точки
По заданным уравнениям её движения»
Для закрепления теоретического материала рекомендуется выполнить курсовое задание К 1.
|
|
|
По заданным уравнениям движения точки М (табл. 2.1) установить вид её траектории и для момента времени t1 найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Таблица 2.1
| Номер варианта | Уравнения движения | t1, c | |
| X = X(t), см | Y = Y(t), см | ||
| 1 | –2·t2 + 3 | –5·t | 0,5 |
| 2 | 4·cos2·(·t/3) + 2 | 4·sin2·(·t/3) | 1 |
| 3 | –cos(·t2/3) + 3 | sin(·t2/3) – 1 | 1 |
| 4 | 4·t + 4 | –4·(t + 1) | 2 |
| 5 | 2·sin(·t/3) | –3·cos(·t/3) + 4 | 1 |
| 6 | 3·t2 + 2 | –4·t | 0,5 |
| 7 | 3·t2–t + 1 | 5·t2 –5·t/3–2 | 1 |
| 8 | 7·sin(·t2/6) + 3 | 2–7·cos(·t2/6) | 1 |
| 9 | –3/(t + 2) | 3·t + 6 | 2 |
| 10 | –4·cos(·t/3) | –2·sin(·t/3)–3 | 1 |
| 11 | –4·t2 + 1 | –3·t | 0,5 |
| 12 | 5·sin2·(·t/6) | –5·cos2·(·t/6) –3 | 1 |
| 13 | 5·cos(·t2/3) | –5·sin(·t2/3) | 1 |
| 14 | –2·t–2 | –2/(t + 1) | 2 |
| 15 | 4·cos(·t/3) | –3·sin(·t/3) | 1 |
| 16 | 3·t | 4·t2 + 1 | 0,5 |
| 17 | 7·sin2·(·t/6) –5 | –7·cos2·(·t/6) | 1 |
| 18 | 1 + 3·cos(·t2/3) | 3·sin(·t2/3) + 3 | 1 |
| 19 | –5t2–4 | 3t | 1 |
| 20 | 2–3·t–6·t2 | 3–3·t/2–3·t2 | 0 |
Окончание табл. 2.1
Дата добавления: 2020-04-25; просмотров: 235; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
