Получение случайной величины, распределенной по заданному закону
Цель работы. Изучение различных законов распределения случайных величин и способов их получения при моделировании случайных процессов.
Теоретическая часть
ГЕНЕРИРОВАНИЕ ДАННЫХ
В программе имитации на ЭВМ часто применяются численные методы (т.е. методы, которые можно запрограммировать на вычислительной машине) генерирования данных. Информацию, используемую в имитационном эксперименте, можно либо ввести в ЭВМ с внешних источников, таких, как перфокарты и магнитные ленты, либо генерировать при помощи специальных программ. Если среди экзогенных переменных модели есть случайные величины с известным вероятностным распределением, то надо построить численный процесс случайного выбора из совокупности с заданным распределением. Результатом повторения этого процесса на цифровой вычислительной машине должно быть такое вероятностное распределение выборочных значений, которое соответствует вероятностному распределению изучаемой, переменной.
При рассмотрении дискретных или непрерывных случайных процессов вводят функцию F(х), называемую кумулятивной функцией распределения величины X . Эта функция задает вероятность того, что случайная величина X принимает значение, не превосходящее число х. Если случайная величина дискретна, т.е. X принимает конечное число значений, то функция F(х) является ступенчатой. Если функция F(х) непрерывна, то ее можно продифференцировать и положить f(x)=dF(х)/dх.Функция f(х) называется функцией плотности вероятностей. Кумулятивную функцию распределения можно определить как 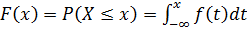 , где F(х) изменяется на отрезке [0,1], а f ( t ) представляет собой значение функции плотности вероятностей случайной величины X при Х= t .
, где F(х) изменяется на отрезке [0,1], а f ( t ) представляет собой значение функции плотности вероятностей случайной величины X при Х= t .
|
|
|
При генерировании случайных величин, имеющих различные функции распределения, используются равномерно распределенные случайные величины. Равномерно распределенные случайные величины будем обозначать через r, 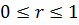 , F ( r )= r .
, F ( r )= r .
В лабораторной работе №1 дан обзор методов генерирования случайных величин, равномерно распределенных на интервале (0,1). Числа, получаемые таким образом, называются псевдослучайными, так как, хотя они и генерируются на ЭВМ при помощи чисто детерминированной рекурсивной формулы, их статистические свойства совпадают со статистическими свойствами чисел, генерированных идеальным случайным механизмом, выбирающим числа из интервала (0,1) независимо и с одинаковой вероятностью. Пока эти псевдослучайные числа удовлетворяют некоторому набору статистических критериев (частотный, сериальной корреляции, интервалов, пар и др.), отражающих свойства идеального случайного механизма, их можно считать «истинно» случайными числами, хотя на самом деле это не так.
|
|
|
Генераторы псевдослучайных чисел в виде подпрограмм есть во всех вычислительных машинах и в большинстве языков программирования.
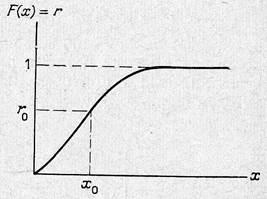
Рисунок 1. Кумулятивная функция распределения
Если требуется генерировать случайные числа xi из некоторой статистической совокупности с функцией плотности вероятностей f(х), то сначала строят кумулятивную функцию распределения F(х) (рис. 1). Так как F(х) изменяется на отрезке [0,1], то, чтобы получить случайные числа с этим распределением, можно генерировать равномерно распределенные случайные числа rи полагать F(х)= r . Ясно, что величина х однозначно определяется из этого соотношения. Следовательно, для конкретного значения r, скажем r0, можно найти величину х, в данном случае х0, связанную с r0 обратной функцией к F(если она известна):
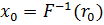
где F-1(r) — обратное отображение величины r, заданной на единичном интервале, в область изменения х. Математически этот метод можно выразить следующим образом: если мы генерируем равномерно распределенные случайные числа и ставим их в соответствие данной функции F(x), то есть
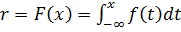 , то
, то
 ,
,
|
|
|
и следовательно 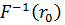 есть случайная величина с функцией плотности вероятностей f(x). Это равносильно выражению величины x через значение r при помощи (2.3). Такая процедура называется методом обратного преобразования.
есть случайная величина с функцией плотности вероятностей f(x). Это равносильно выражению величины x через значение r при помощи (2.3). Такая процедура называется методом обратного преобразования.
Самым простым непрерывным распределением является, по-видимому, распределение с функцией плотности вероятностей, постоянной на интервале (а, b ) и равной нулю вне его. Эта функция плотности вероятностей определяет так называемое равномерное, или прямоугольное, распределение. Равномерное распределение часто применяется в имитационных методах, во-первых, потому, что оно просто, а во-вторых, потому, что его можно использовать для генерирования случайных величин с другими вероятностными распределениями.
Функция плотности вероятностей равномерного распределения имеет вид
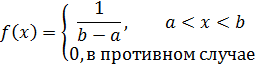
Здесь X — случайная величина, определенная на интервале (а, b ), График равномерного распределения изображен на рис, 2.2,
Кумулятивная функция распределения F(x)равномерно распределенной случайной величины X равна
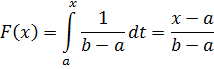
Для имитации равномерного распределения на интервале (а, b ) сначала в соответствии с формулой (2.2) надо получить обратное преобразование для (2.6):
х=а+( b —а) r , 0<г<1. (2.7)
|
|
|
Далее генерируются случайные числа, равномерно распределенные в интервале (0,1). Каждое случайное число r однозначно определяет реализацию равномерно распределенной случайной величины X.
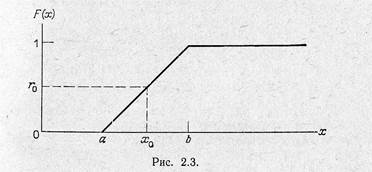
На рис. 2.3 видно, что каждому значению r соответствует единственное значение х. Так, конкретное значение кумулятивной функции распределения, равное r0, определяет значение х, равное х0. Очевидно, что процедуру можно повторять нужное число раз, и каждый раз она будет давать новое значение х.
Основные виды распределений случайных величин, используемые в моделировании
1. Равномерное распределение (прямоугольное распределение).
Функция плотности вероятности этого распределения задает вероятность того, что некоторое значение попадает в заданный интервал [a,b], и эта вероятность пропорциональна длине этого интервала.
Это распределение применяют часто в условиях полного отсутствия информации о случайной величине кроме ее предельных значений. Равномерное распределение характеризуется
a. функцией плотности вероятности: f(x)=1/(b-a), a£x£b;
b. математическим ожиданием: M=(а+b)/2;
c. дисперсией: D=(b - a)2/12.
2. Треугольное распределение
Для этого распределения определяют 3 величины: минимум а, максимум b, и моду m ( 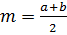 ). График функции плотности вероятности состоит из двух отрезков прямых, один из которых возрастает при изменении х от минимального значения до моды, а другой убывает при изменении х от значения моды до максимума. Это распределение используется тогда, когда известно наиболее вероятное значение на некотором интервале и предполагается кусочно-линейный характер функции плотности вероятности.
). График функции плотности вероятности состоит из двух отрезков прямых, один из которых возрастает при изменении х от минимального значения до моды, а другой убывает при изменении х от значения моды до максимума. Это распределение используется тогда, когда известно наиболее вероятное значение на некотором интервале и предполагается кусочно-линейный характер функции плотности вероятности.
Треугольное распределение характеризуется:
a. 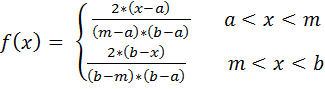
b. M = (a + b + m)/3;
c. 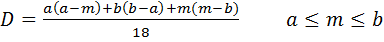
3. Экспоненциальное распределение
Если вероятность того, что один и только один результат наступит на интервале Dt пропорциональна Dt, и если наступление результата не зависит от наступления других результатов (т.е. процесс характеризуется отсутствием последействия), то величины интервалов между результатами распределены экспоненциально.
Это распределение характеризуется функцией плотности распределения: 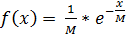 , где х>0, М – математическое ожидание; D=М2.
, где х>0, М – математическое ожидание; D=М2.
4. Распределение Пуассона
Это распределение является дискретным и связано обычно с числом результатов за определенный период времени. Если интервалы между появлением результатов распределены экспоненциально, то число, появившихся результатов в данный отрезок времени будет распределено в соответствии с распределением Пуассона.
Характеристики распределения:
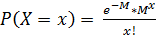 , x=0,1,2,...;
, x=0,1,2,...;
D = М.
5. Нормальное (гауссово) распределение
Широко применяется в моделировании. Это определено значением центральной предельной теоремы, которая утверждает, что при весьма нестрогих условиях распределение средней величины или суммы N- независимых наблюдений из любого распределения стремится к нормальному по мере увеличения N. (Центральные предельные теоремы — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения. [Википедия])
Распределение характеризуется 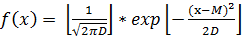 , xÎ(–¥, +¥).
, xÎ(–¥, +¥).
M=m;
D=s2.
6. Логарифмическое нормальное распределение
Это распределение такой случайной величины, натуральный логарифм которой нормально распределен. Оно пригодно для моделирования мультипликативных процессов так же, как нормальное - для аддитивных.
Распределение характеризуется функцией плотности вероятности: 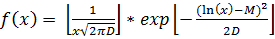
7. Биномиальное распределение .
Это распределение вероятностей случайной величины X с целочисленными значениями х=0,1,2,...,n.
Пусть проводится эксперимент, в результате которого нас интересует, произошло событие А или не произошло. Случай, в котором событие А произошло, назовем успехом, вероятность этого события Р(А) = р. Если же событие А не произошло, то его вероятность Р(`А) = 1 – р = q. Предположим теперь, что серия независимых испытаний такого типа проводится n раз. Нас интересует вероятность события, состоящего в том, что успех произошел ровно m раз, или вероятность того, что дискретная случайная величина Х, равная числу успехов, примет значение x. Решение этой задачи имеет вид:
Функция вероятности характеризуется формулой: 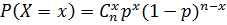 , где
, где 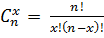 ; 0£p£1 ; n≥1.
; 0£p£1 ; n≥1.
Функция распределения: 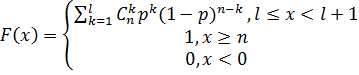
Математическое ожидание: M(x) = n*p
Дисперсия: D(x) = n*p*(1-p).
8. Распределение Вейбулла
Это распределение характеризуется функцией распределения: 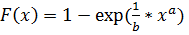 , где b - параметр масштабирования, a -параметр кривизны.
, где b - параметр масштабирования, a -параметр кривизны.
Распределение Вейбула часто используется в теории надежности для описания времени безотказной работы приборов.
9. Распределение Коши
Это распределение характеризуется плотностью вероятности:
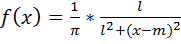 , где l и m (мода и медиана) - параметры данной функции, –¥<m<+¥ и l>0.
, где l и m (мода и медиана) - параметры данной функции, –¥<m<+¥ и l>0.
10. Распределение Эрланга
Это распределение характеризуется плотностью вероятности
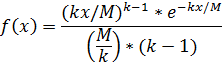
где k > 0 - коэффициент Эрланга, m - математическое ожидание.
Дата добавления: 2020-04-25; просмотров: 246; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
