МЕТОДЫ ПРОВЕРКИ ЧИСЕЛ НА ПРОСТОТУ
Тестом простоты (или проверкой простоты) называется алгоритм, который, приняв на входе число N, позволяет либо не подтвердить предположение о составности числа, либо точно утверждать его простоту. Во втором случае он называется истинным тестом простоты. Таким образом, тест простоты представляет собой только гипотезу о том, что если алгоритм не подтвердил предположение о составности числа N, то это число может являться простым с определённой вероятностью. Это определение подразумевает меньшую уверенность в соответствии результата проверки истинному положению вещей, нежели истинное испытание на простоту, которое дает математически подтвержденный результат.
Рисунок 4.1
Тест Ферма
Тест простоты Ферма в теории чисел — это тест простоты натурального числа n, основанный на малой теореме Ферма.
Если n — простое число, то оно удовлетворяет сравнению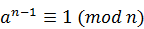 
для любого a, которое не делится на n. Выполнение сравнения
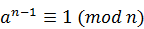является необходимым, но не достаточным признаком простоты числа. То есть, если найдётся хотя бы одно a, для которого
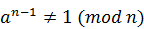то число n — составное; в противном случае ничего сказать нельзя, хотя шансы на то, что число является простым, увеличиваются. Если для составного числа n выполняется сравнение
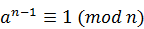, то число n называют псевдопростым по основанию a . При проверке числа на простоту тестом Ферма выбирают несколько чисел a. Чем больше количество a, для которых 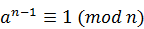, тем больше шансы, что число n простое. Однако существуют составные числа, для которых сравнение 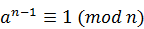выполняется для всех a, взаимно простых с n — это числа Кармайкла. Чисел Кармайкла — бесконечное множество, наименьшее число Кармайкла — 561. Тем не менее, тест Ферма довольно эффективен для обнаружения составных чисел.
|
|
|
Тест Соловея-Штрассена
Тест Соловея — Штрассена — вероятностный тест простоты, открытый в 1970-х годах Робертом Мартином Соловеем совместно с Фолькером Штрассеном. Тест всегда корректно определяет, что простое число является простым, но для составных чисел с некоторой вероятностью он может дать неверный ответ. Основное преимущество теста заключается в том, что он, в отличие от теста Ферма, распознает числа Кармайкла как составные.
Алгоритм Соловея — Штрассена параметризуется количеством раундов k. В каждом раунде случайным образом выбирается число a < n. Если НОД(a,n) > 1, то выносится решение, что n составное. Иначе проверяется справедливость сравнения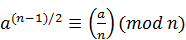 
. Если оно не выполняется, то выносится решение, что n — составное. Если это сравнение выполняется, то a является свидетелем простоты числа n. Далее выбирается другое случайное a и процедура повторяется. После нахождения k свидетелей простоты в k раундах выносится заключение, что n является простым числом с вероятностью 
.
|
|
|
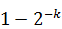Тест Миллера — Рабина
Как и тесты Ферма и Соловея — Штрассена, тест Миллера — Рабина опирается на проверку ряда равенств, которые выполняются для простых чисел. Если хотя бы одно такое равенство не выполняется, это доказывает что число составное.
Для теста Миллера — Рабина используется следующее утверждение:
Рисунок 4.2
Если это утверждение (условие 1 или 2) выполняется для некоторых чисел а и n (не обязательно простого), то число a называют свидетелем простоты числа n по Миллеру, а само число n — вероятно простым. (При случайно выбранном a вероятность ошибочно принять составное число за простое составляет 25 %, но её можно уменьшить, выполнив проверки для других a.
В случае когда выполняется контрапозиция доказанного утверждения, то есть если найдется число a такое, что:
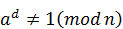
и
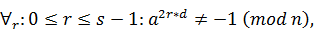
то число n не является простым. В этом случае число a называют свидетелем того, что число n составное.
У нечётных составных чисел n существует, согласно теореме Рабина, не более (n)/4 свидетелей простоты, n— функция Эйлера, таким образом вероятность того, что случайно выбранное число a окажется свидетелем простоты, меньше ¼.
|
|
|
Идея теста заключается в том, чтобы проверять для случайно выбранных чисел a<n, являются ли они свидетелями простоты числа n. Если найдётся свидетель того, что число составное, то число действительно является составным. Если было проверено k чисел, и все они оказались свидетелями простоты, то число считается простым. Для такого алгоритма вероятность принять составное число за простое будет меньше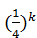 
Для проверки больших чисел принято выбирать числа a случайными, так как распределение свидетелей простоты и свидетелей составного числа среди чисел 1, 2, …, n − 1 заранее неизвестно. В частности Арнольтприводит 397-разрядное составное число, для которого все числа меньше 307 являются свидетелями простоты.
Из рассмотренных выше теорем на проверку простых чисел, мы можем сделать вывод о том, что теорема Ферма дает наиболее точные ответы на вопрос о простоте числа, с наименьшей погрешностью.
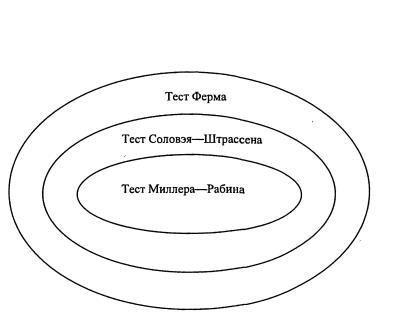
Рисунок 4.3
Дата добавления: 2020-04-25; просмотров: 756; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!