Инвариантность типа уравнения
Задания и методические указания
Для самостоятельной работы студентов
Для успешного усвоения учебного курса и выполнения домашнего задания студенту необходимо самостоятельно выполнить следующие этапы:
1. Проработка лекций, самостоятельная работа с учебной литературой по теме лекции, используя в том числе онлайн-ресурс Образовательный портал НИЯУ МИФИ online.mephi.ru.
2. Подготовить конспект лекций
3. Разобрать задачи по теме лекций.
4. Решить указанные задания для самостоятельной работы.
5. Прислать скан или фото решенных задач и конспектов (в разборчивом виде) Катаевой Галине Валентиновне на электронную почту: galvk@mail.ru с пометкой «МФ-31»
Срок выполнения домашнего задания №1: 01.04.2020 г.
Срок выполнения домашнего задания №2: 08 .04.2020 г.
Перечень основной и дополнительной учебной литературы:
1. Пискунов Н. С. Дифференциальное и интегральное исчисления. Т. 2. - М.: Интеграл - Пресс, 2004.
2. Тихонов А. Н., Самарский А. А. Уравнения математической физики. - М.: Наука, 2004.
3. Владимиров В.С. Сборник задач по уравнениям математической физики М.: Физматлит, 2003
ЛЕКЦИИ
Лекция 1 ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ
УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО ТИПА
Рассмотрим дифференциальное уравнение второго порядка в частных производных:
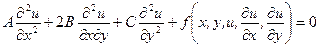. (2.1)
Если А, В, С – функции от x, y, u, 
, 
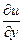, то уравнение квазилинейное.
Если А, В, С – функции от x, y, а функция
|
|
|
,
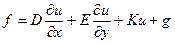где D, E, K – функции от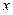 
, 
; 
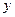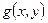– возмущение, то уравнение (2.1) – линейное.
Если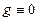 
, то (2.1) – линейное однородное,
если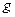 
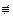
, то (2.1) – линейное неоднородное
Пусть (2.1) – линейное уравнение. Обозначим 
, где А, В, С в общем случае зависят от x, y. Тогда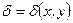 
называется дискриминантом уравнения (2.1).
Если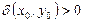 
, 
, 
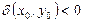, то уравнение (2.1) называется соответственно уравнением гиперболического, параболического или эллиптического типа в точке 
.
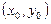Если 
, 
, 
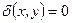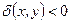для любой точки 
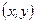из области 
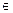R2, то уравнение (2.1) называется соответственно уравнением гиперболического, параболического или эллиптического типа в области .
В качестве примеров рассмотрим:
.
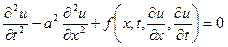В данном уравнении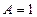 
, 
, 
, 
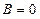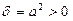, то есть это уравнение гиперболического типа, описывающее колебательные процессы.
.
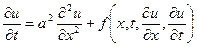Видим, что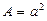 
, 
, 
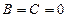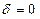. Таким образом перед нами уравнение параболического типа, описывающее процессы теплопроводности и диффузии.
3. 
.
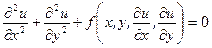Здесь , ,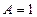 
, 
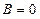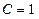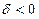. Таким образом перед нами уравнение эллиптического типа, описывающее состояния системы, которые не зависят от времени.
В качестве иллюстрации рассмотрим уравнение:
.
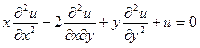В этом уравнении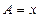 
, 
, 
, 
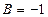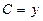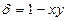. Дискриминант 
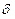зависит от , .
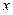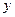Тогда:
а) если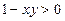 
, то есть 
, то имеем уравнение гиперболического типа;
|
|
|
б) если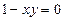 
, то есть 
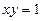, то имеем уравнение параболического типа;
в) если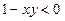 
, то есть 
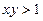, то имеем уравнение эллиптического типа.
Графически случаи а), б), в) в области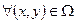 
можно представить следующим образом:
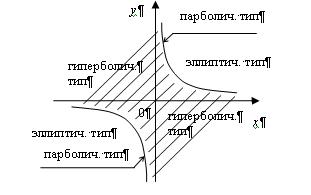
Инвариантность типа уравнения
Введём новые независимые переменные:
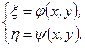(4.1)
Якобиан преобразования (4.1) будет иметь вид:
,
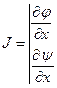
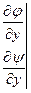где обозначено, например, 
.
Если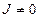 
, то преобразование называется невырожденным.
Докажем, что при невырожденном преобразовании тип уравнения (2.1) не меняется.
Доказательство:
Считаем все производные:
,
,
,
,
.
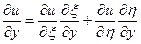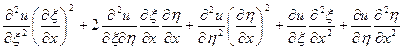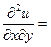
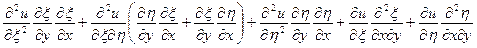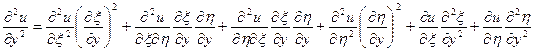Здесь учтено, что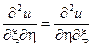 
для непрерывной на области 
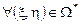функции 
.
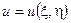Подставим найденные производные в уравнение (2.1):
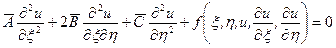, (4.2)
,
,
.
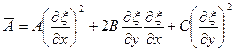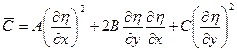Тогда для дискриминанта уравнения (4.2) получаем:
.
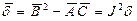Видим, что знак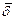 
уравнения (4.2) и знак 
уравнения (2.1) одинаковый. Поэтому тип уравнения не изменился:
1) 
, 
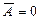гиперболический Þ 
;
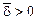2) , 
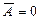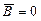параболический Þ 
;
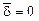3) 
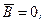
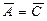эллиптический Þ 
.
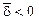Утверждение доказано.
Уравнение характеристик
Рассмотрим уравнение вида:
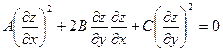. (5.1)
|
|
|
Данное уравнение является уравнением в частных производных первого порядка.
Вместе с уравнением (5.1) рассмотрим обыкновенное дифференциальное уравнение:
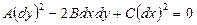. (5.2)
Его формальное решение для дифференциала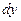 
имеет вид:
,
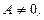
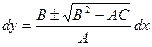, (5.2 а)
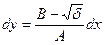. (5.2 б)
В свою очередь решение уравнений (5.2 а) и (5.2 б) находим в виде общих интегралов:
.
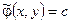Лемма. Если 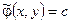- общий интеграл уравнения (5.2), то функция 
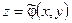есть частное решение уравнения (5.1).
Данную лемму приводим без доказательства.
Функция 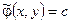называется характеристикой уравнения (5.2). А уравнения (5.1) и (5.2) называются уравнениями характеристик.
Дата добавления: 2020-04-25; просмотров: 86; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!