Метод покоординатного спуска.
Кафедра «Промышленная автоматика»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
По выполнения практических работ по дисциплине
«Теория принятия решений» для студентов, обучающихся по направления подготовки 15.03.04 Автоматизация технологических процессов и производств
Кумертау 2018
Содержание
| Порядок оформления отчета | 3 |
| Практическая работа № 1. Одномерная оптимизация | 4 |
| Практическая работа № 2. Многомерная оптимизация | 10 |
| Практическая работа № 3. Линейное программирование | 14 |
| Список литературы | 28 |
Порядок оформления отчета
Отчет должен иметь титульный лист и включать следующие разделы:
1) цель работы;
2) задание;
3) технологию работы (по каждому пункту);
4) выполнение задания с результатами по каждому пункту;
5) выводы по работе.
Практическая работа № 1
Одномерная оптимизация
Цель работы: получить практические навыки нахождения оптимального решения одномерных задач методами золотого сечения и дихотимии.
Основные теоретические сведения
Метод золотого сечения. Для произвольного отрезка [a , b] выражения для пробных точек примут вид
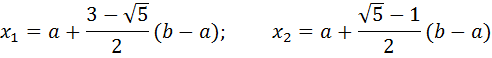
| (1) |
На каждой итерации отрезок поиска точки минимума уменьшается в одном и том же отношении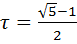 
, поэтому в результате n итераций его длина становится 
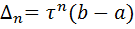. Таким образом, точность определения точки после итераций находится из равенства
|
|
|
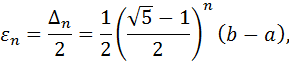
| (2) |
а условием окончания поиска точки x ∗ с точностью ε служит неравенство ε ≤ εn.
Алгоритм метода золотого сечения следующий.
Шаг 1. Определить x1 и x2 по формуле (1). Вычислить f ( x1) и f ( x2). Положить ,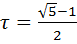 
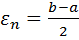. Перейти к шагу 2.
Шаг 2. Проверка окончания поиска: если εn>ε, то перейти к шагу 3, иначе − к шагу 4.
Шаг 3. Переход к новому отрезку и новым пробным точкам. Если f ( x1)≤ f ( x2), то положить b = x2, x2=x1, f ( x1)=f ( x2), x1= b –τ( b - a ) и вычислить f ( x1), иначе − положить a = x1, x1=x2, f ( x1)=f ( x2), x2= b –τ( b - a ) и вычислить f ( x2). Положив εn=τεn, перейти к шагу 2.
Шаг 4. Окончание поиска: положить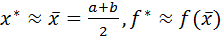 
.
Метод дихотомии. В соотвествии с даннымметодом выбираются пробные точки, которые располагаются близко к середине очередного отрезка [a , b], т.е.
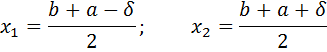
| (3) |
где δ − малое число.
В конце вычислений методом дихотомии в качестве приближенного значения берут середину последнего из найденных отрезков [a , b], убедившись предварительно, что достигнуто неравенство
| (4) |
Алгоритм метода деления отрезка пополам следующий.
Шаг 1. Определить x1 и x2 по формуле (3) и вычислить f ( x1) и f ( x2). Перейти к шагу 2.
Шаг 2. Сравнить f ( x1) и f ( x2). Если f ( x1)≤ f ( x2), то перейти к отрезку [a, x2], положив b = x2, иначе − к отрезку [x1, b], положив a=x1. Перейти к шагу 3.
|
|
|
Шаг 3. Найти достигнутую точность εn=(a−b)/2 (здесь n − номер итерации). Если εn>ε, то перейти к следующей итерации, вернувшись к шагу 1. Если εn ≤ε, то завершить поиск x∗.
Пример выполнения
Решить задачу методами золотого сечения и дихотомии f ( x )= x 4 + e - x →min, x∈[0,1], с точностью до ε=0,1.
Метод золотого сечения
Определим пробные точки x1 и x2:
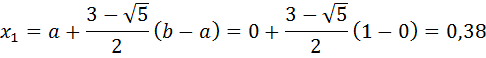
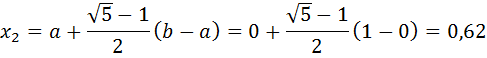
Вычислим f ( x1) и f ( x2):
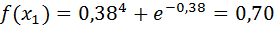
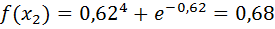
Проверим точность поиска:
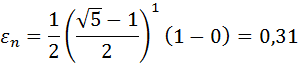
Так как εn>ε, то перейти к следующей итерации. f ( x2)< f ( x1), то положим a = x1, x1=x2, f ( x1)=f ( x2), x2= b –τ( b - a ) и вычислить f ( x2).
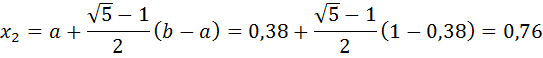
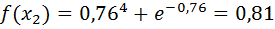
Проверим точность поиска:
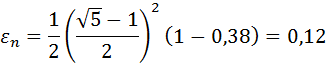
Так как εn>ε, то перейти к следующей итерации. f ( x1)< f ( x2), то положим b = x2, x2=x1, f ( x1)=f ( x2), x1= b –τ( b - a ) и вычислить f ( x1).
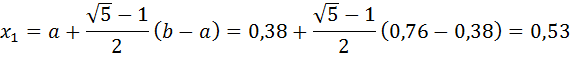
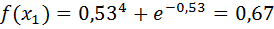
Проверим точность поиска:
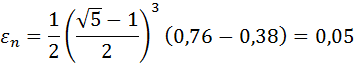
Так как εn<ε, поиск окончен, точка оптимума x *=0,53.
| Номер итерации | a | b | εn | x1 | x2 | f(x1) | f(x2) | Сравнение |
| 1 | 0 | 1 | 0,3090 | 0,3820 | 0,6180 | 0,7038 | 0,6849 | f(x2)<f(x1) |
| 2 | 0,3820 | 1 | 0,1180 | 0,6180 | 0,7639 | 0,6849 | 0,8064 | f(x1)<f(x2) |
| 3 | 0,3820 | 0,7639 | 0,0451 | 0,5279 | 0,6180 | 0,6675 | 0,6849 |
Метод дихотомии.
Определим пробные точки x1 и x2, для этого примем δ=0,02:
|
|
|
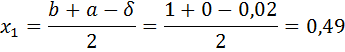
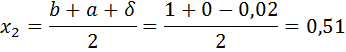
Вычислим f ( x1) и f ( x2):
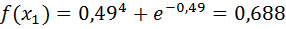
Проверим точность поиска:
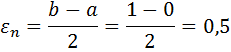
Так как εn>ε, то перейти к следующей итерации. f ( x2)< f ( x1), то положим a = x1, b=1 и вычислить x1, x2, f ( x1), f ( x2).
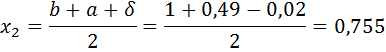
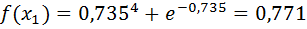
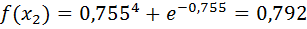
Проверим точность поиска:
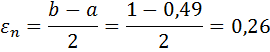
Так как εn>ε, то перейти к следующей итерации. f ( x1)< f ( x2), то положим a =0,49, b = x2 и вычислить x1, x2, f ( x1), f ( x2).
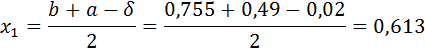
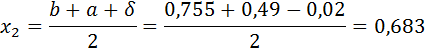
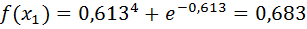
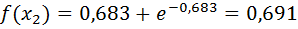
Проверим точность поиска:
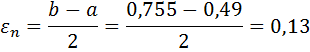
Так как εn>ε, то перейти к следующей итерации. f ( x1)< f ( x2), то положим a =0,49, b = x2 и вычислить x1, x2, f ( x1), f ( x2).
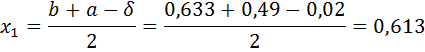
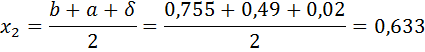
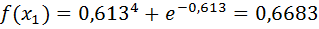
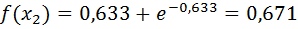
Проверим точность поиска:
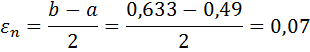
Так как εn<ε, поиск окончен, точка оптимума x *=0,57.
| Номер итерации | a | b | εn | x1 | x2 | f(x1) | f(x2) | Сравнение |
| 1 | 0 | 1 | 0,5000 | 0,4900 | 0,5100 | 0,6703 | 0,6681 | f(x2)<f(x1) |
| 2 | 0,4900 | 1 | 0,2550 | 0,7350 | 0,7550 | 0,7713 | 0,7949 | f(x1)<f(x2) |
| 3 | 0,4900 | 0,7550 | 0,1325 | 0,6125 | 0,6325 | 0,6827 | 0,6913 | f(x1)<f(x2) |
| 4 | 0,4900 | 0,6325 | 0,0713 | 0,5513 | 0,5713 | 0,6686 | 0,6713 | f(x1)<f(x2) |
Варианты заданий
На отрезке [-2, 2] найти точку минимума (максимум) функции f ( x ) с точностью ε=0,01 методами золотого сечения и дихотомии. Сравнить эффективность методов.
| Номер вариа-нта | f ( x ) | Характер экстре-мума | Номер вариа-нта | f ( x ) | Характер экстре-мума |
| 1. |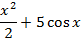 
| min | 2. |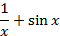 
| min |
| 3. |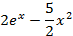 
| min | 4. |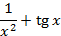 
| min |
| 5. |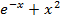 
| min | 6. |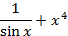 
| min |
| 7. |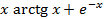 
| min | 8. |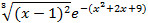 
| min |
| 9. |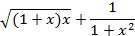 
| min | 10. |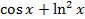 
| min |
| 11. |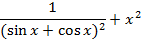 
| min | 12. | 
| min |
| 13. |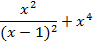 
| min | 14. |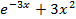 
| min |
| 15. |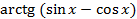 
| max | 16. |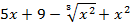 
| min |
| 17. |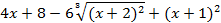 
| min | 18. |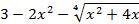 
| min |
| 19. | 
| max | 20. |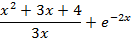 
| min |
| 21. |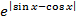 
| max | 22. |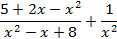 
| min |
| 23. | 
| min | 24. |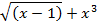 
| min |
| 25. | 
| max | 26. |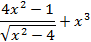 
| min |
| 27. |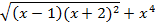 
| max | 28. |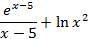 
| min |
| 29. |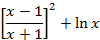 
| min | 30. | 
| min |
| 31. |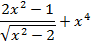 
| min | 32. |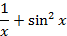 
| min |
| 33. |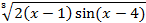 
| min | 34. |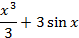 
| min |
| 35. |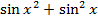 
| max | 36. | 
| min |
| 37. |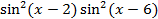 
| max | 38. | 
| min |
| 39. | 
| min | 40. |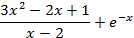 
| min |
| 41. |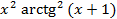 
| min | 42. |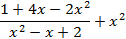 
| min |
| 43. |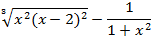 
| max | 44. |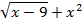 
| min |
| 45. |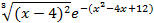 
| max | 46. |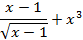 
| min |
| 47. |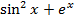 
| min | 48. |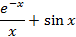 
| min |
| 49. |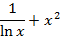 
| min | 50. | 
| min |
|
|
|
Практическая работа № 2
Многомерная оптимизация
Цель работы: получить практические навыки нахождения оптимального решения многомерных задач методами покоординатного и наискорейшего спуска.
Теоретические сведения
Метод покоординатного спуска. Сущность метода заключается в поочередном изменении координат (направления поиска) x 1 , x 2 , …, xn и определение частных производных вида:
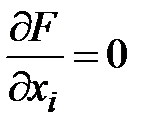
Первоначально изменяется координата x 1 в направлении уменьшения величины градиента ∂ F /∂ x 1 целевого критерия, при неизменных значениях остальных координат. После достижения точки, в которой значение градиента ∂ F /∂ x 1 обращения в нуль, производится изменение координаты x 2 в сторону уменьшения градиента ∂ F /∂ x 2 целевого критерия, при постоянных значениях остальных координат. Далее следует аналогичный поиск по координате x 3 и т.д.
После осуществления поиска по всем направлениям вновь происходит изменение координаты x 1 до обращения в нуль ∂ F /∂ x 1, и цикл повторяется. Процесс поиска завершается, когда все составляющие ∂ F /∂ xi будут равны нулю.
Метод наискорейшего спуска. Сущность метода наискорейшего спуска заключается в следующем. В начальной точке производится определение направление градиента. Движение в направлении уменьшения градиента ∂ F /∂ l целевого критерия происходит до тех пор, пока частная производная ∂ F /∂ l, взятая вдоль указанного направления, не обратится в нуль. В точке, где частная производная ∂ F /∂ l обращается в нуль, вновь определяется направление градиента и происходит движение вдоль определенного направления вектора до обращения в нуль частной производной, взятой по новому направлению градиента и т.д..
Порядок выполнения
Минимизировать функцию f ( x , y )=10* x 2 +1,4* y +0,1 методами покоординатного и наискорейшего спуска. Начальная точка поиска x=-1, y=-1, точность ε=0,1.
Метод покоординатного спуска.
| x | y | f(x,y) |
| -1 | -1 | 8,7 |
| -0,9 | -1 | 6,8 |
| -0,8 | -1 | 5,1 |
| -0,7 | -1 | 3,6 |
| -0,6 | -1 | 2,3 |
| -0,5 | -1 | 1,2 |
| -0,4 | -1 | 0,3 |
| -0,3 | -1 | -0,4 |
| -0,2 | -1 | -0,9 |
| -0,1 | -1 | -1,2 |
| 0 | -1 | -1,3 |
| 0,1 | -1 | -1,2 |
| 0 | -0,9 | -1,16 |
Метод наискорейшего спуска.
| x | y | f(x,y) |
| -1 | -1 | 8,7 |
| -0,9 | -1 | 6,8 |
| -1 | -0,9 | 8,84 |
| -0,9 | -0,9 | 6,94 |
| -0,8 | -1 | 5,1 |
| -0,7 | -1 | 3,6 |
| -0,6 | -1 | 2,3 |
| -0,5 | -1 | 1,2 |
| -0,4 | -1 | 0,3 |
| -0,3 | -1 | -0,4 |
| -0,2 | -1 | -0,9 |
| -0,1 | -1 | -1,2 |
| 0 | -1 | -1,3 |
| 0,1 | -1 | -1,2 |
| -0,1 | -0,9 | -1,06 |
| 0 | -0,9 | -1,16 |
| 0,1 | -0,9 | -1,06 |
Минимум функции f ( x , y )=10* x 2 +1,4* y +0,1 определяется в точке [0, -1] и равен -1,3.
Варианты заданий
Минимизировать функцию f ( x , y ) методами покоординатного и наискорейшего спуска. Начальная точка поиска x=-1, y=-1, точность ε=0,1.
1. f ( x , y )= ax 2 + by + c
| Номер варианта | a | b | c | Номер варианта | a | b | c |
| 1. | 1,0 | –1,4 | 0,01 | 8. | 8,0 | –0,7 | 0,02 |
| 2. | 2,0 | –1,3 | 0,03 | 9. | 9,0 | –0,6 | 0,04 |
| 3. | 3,0 | –1,2 | 0,05 | 10. | 10,0 | –0,5 | 0,06 |
| 4. | 4,0 | –1,1 | 0,07 | 11. | 11,0 | –0,4 | 0,08 |
| 5. | 5,0 | –1,0 | 0,09 | 12. | 12,0 | –0,3 | 0,10 |
| 6. | 6,0 | –0,9 | 0,11 | 13. | 13,0 | –0,2 | 0,12 |
| 7. | 7,0 | –0,8 | 0,13 | 14. | 14,0 | –0,1 | 0,14 |
2. f(x,y)=ax2+by2-c
| Номер варианта | a | b | c | Номер варианта | a | b | c |
| 15. | 1,0 | –1,2 | 0,01 | 21. | 7,0 | –0,6 | 0,00 |
| 16. | 2,0 | –1,1 | 0,03 | 22. | 8,0 | –0,5 | 0,02 |
| 17. | 3,0 | –1,0 | 0,05 | 23. | 9,0 | –0,4 | 0,04 |
| 18 | 4,0 | –0,9 | 0,07 | 24. | 10,0 | –0,3 | 0,06 |
| 19. | 5,0 | –0,8 | 0,09 | 25. | 11,0 | –0,2 | 0,08 |
| 20. | 6,0 | –0,7 | 0,11 | 26. | 12,0 | –0,1 | 0,10 |
3. f(x,y)=ax2+eby+c
| Номер варианта | a | b | c | Номер варианта | a | b | c |
| 27. | 1,1 | –0,22 | 0,31 | 33. | 1,7 | –0,16 | 0,21 |
| 28. | 1,2 | –0,21 | 0,32 | 34. | 1,8 | –0,15 | 0,22 |
| 29. | 1,3 | –0,20 | 0,33 | 35. | 1,9 | –0,14 | 0,23 |
| 30. | 1,4 | –0,19 | 0,34 | 36. | 2,0 | –0,13 | 0,24 |
| 31. | 1,5 | –0,18 | 0,35 | 37. | 2,1 | –0,12 | 0,25 |
| 32. | 1,6 | –0,17 | 0,36 | 38. | 2,2 | –0,11 | 0,26 |
4. 
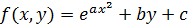
| Номер варианта | a | b | c | Номер варианта | a | b | c |
| 39. | 1,0 | 0,25 | 0,01 | 45. | 4,0 | 1,75 | 0,64 |
| 40. | 1,5 | 0,50 | 0,02 | 46. | 4,5 | 2,00 | 1,28 |
| 41. | 2,0 | 0,75 | 0,04 | 47. | 5,0 | 2,25 | 2,56 |
| 42. | 2,5 | 1,00 | 0,08 | 48. | 5,5 | 2,50 | 5,12 |
| 43. | 3,0 | 1,25 | 0,16 | 49. | 6,0 | 3,00 | 10,24 |
| 44. | 3,5 | 1,50 | 0,32 | 50. | 6,5 | 3,25 | 20,48 |
Практическая работа № 3
Линейное программирование
Цель работы: получить практические навыки решения задачи линейного программирования симплекс-методом.
Дата добавления: 2020-04-08; просмотров: 391; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!