Распределение центров базисных функций
Хорошо, к нашему сожалению, теперь каноническая система не сходится к цели линейно, как предполагалось выше. Вот сравнение линейного затухания и экспоненциального затухания реальной системы:
Рис.6.
Это – проблема, т.к. наши базисные функции активируются в зависимости от x. Если бы система была линейной, активации базисных функций были бы хорошо распределены, и система бы сходилась к цели. Но x – нелинейная функция от времени, и графики активаций базисных функций, как функции от времени, для большинства реальных систем активируются незамедлительно, поскольку система движется быстро вначале, а затем активации растягиваются по мере замедления в конце:
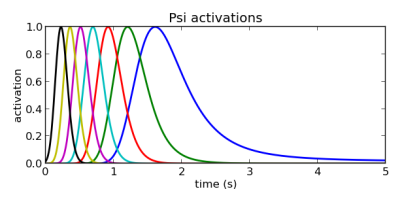
Рис.7.
В интересах более равномерного распределения для базисных функций во времени (чтобы наша функция усилия всё ещё могла перемещать систему по интересующим путям ближе к цели), нужно более тщательно выбирать центры Гауссианов. Если посмотреть на x в зависимости от времени, можно выбрать моменты, в которые нам бы хотелось, чтобы Гауссианы были активированы, и затем найти прообраз – соответствующее значение x, которые дают нам эти активации в то время.
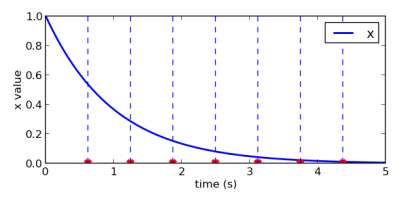
Рис.8.
Красные точки – моменты времени, где нам хотелось бы, чтобы были расположены центры Гауссианов, а синяя линия – это наша каноническая система x. Следуя пунктирным линиям до соответствующих значений x, видно, в каких значениях x должны быть центры Гауссианов. Кроме того, нужно немного беспокоиться о ширине каждого Гауссиана, потому что активированные позже будут активны в течение более длительных периодов времени. Чтобы их выровнять, более поздние ширины базисных функций должны быть меньше. Благодаря очень неаналитическому методу проб и ошибок я пришёл к выводу, что дисперсия (ширина) должна вычисляться так:
|
|
|
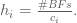
Т.е. дисперсия базисной функции i равна количеству базисных функций, делённому на центр этой базисной функции. Посчитав это, можно сгенерировать центры наших базовых функций, которые хорошо разнесены:
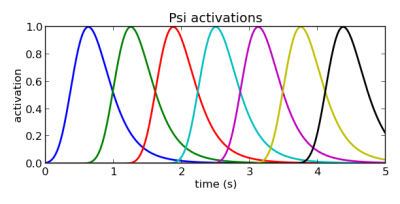
Рис.9.
Временное масштабирование
Опять же, обобщаемость системы действительно важна. Есть 2 очевидных вида масштабирования: временное и пространственное.
Временное масштабирование – когда хотелось бы иметь возможность следовать однажды предсказанной траектории на разных скоростях – иногда быстро, иногда медленно, но всегда следуя одному пути.
Добавим в динамику системы ещё один коэффициент временного масштабирования. Учитывая, что динамика нашей системы:
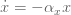
Чтобы дать временную гибкость, можно добавить коэффициент τ:
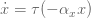
Используем τ2, т.к. 
– это вторая производная. Теперь, чтобы замедлить систему, нужно установить τ между 0 и 1, а чтобы ускорить её – установить τ >1.
|
|
|
Имитация желаемого пути
Коэффициент силового влияния (forcing term) может заставить систему пойти по странному пути, во время её приближения к целевой точке вместе с временным и пространственным масштабированием.
Как настроить систему, чтобы она следовала указанной траектории?
Было бы идеально, если можно было бы:
1. показать системе путь, по которому она должна идти,
2. система имела возможность вычислять силы, необходимые для следования указанной траектории (т.е. действовать в обратном порядке),
3. система умела бы генерировать траекторию в любое время, когда захотим.
В конечном итоге, всё это – довольно простой процесс.
Мы контролируем коэффициент силового влияния (forcing term), который обеспечивает ускорение системы. Поэтому сначала нужно взять желаемую траекторию 
(где жирным обозначен вектор – в данном случае временной ряд искомых точек на траектории) и дважды продифференцировать его, чтобы получить ускорение:
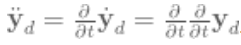
Как только получена желаемая траектория ускорения, нужно устранить влияние базисных точечных аттракторов системы. Уравнение выше для точного определения ускорения, вызванного точечными аттракторами в каждый момент времени:
|
|
|
Таким образом, вычислить какой коэффициент силового влияния требуется, чтобы сгенерировать траекторию, можно по формуле:
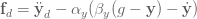
Откуда известно, что коэффициент силового влияния состоит из взвешенной суммы базисных функций, которые активируются во времени, поэтому можно использовать метод оптимизации, такой как локально-взвешенная регрессия(locally weighted regression), чтобы выбрать веса наших базисных функций, чтобы функция усилия соответствовала желаемой траектории 
.
Локально-взвешенная регрессия должна минимизировать выражение:
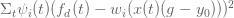
и её решением (которое не буду выводить здесь, оно проработано в статье Schaal 1998 г.) является:
где
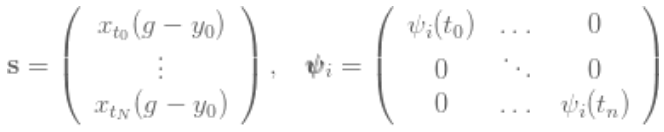
Теперь имеется всё, что нужно, чтобы начать делать первичные дискретные DMP.
Дата добавления: 2019-11-16; просмотров: 80; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!