Геометрическое представление комплексных чисел.
Для геометрического представления к.ч. используют точки и векторы координатной плоскости. В качестве к.ч.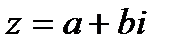 
используют точку с абсциссой а и ординатой b.
|
| у |
| 0 |
| -1 |
| Ö3 |
| М(Ö3;-1) |
| j |
| х,r |
Если к.ч. 
0, то его можно представить в виде
тригонометрическая форма к.ч,
где 
модуль к.ч
Угол 
- угол, образованный 
с осью OX, назначенный аргументом к.ч. и обознается 
, причем tg 
Чтобы перейти от алгебраической формулы к.ч к тригонометрической и обратно, необходимо сделать следующие преобразования:
, 
, 
Пример.
. Составить тригонометрическую форму к.ч. и изобразить его?
Действия над к.ч. в тригонометрической форме:
Показательная форма комплексного числа.
Кроме алгебраической и тригонометрической формы к.ч. имеют также показательную форму: 
Если 
, то 
Если 
, то комплексно-сопряженное имеет вид: 
.
Сравним записи комплексных чисел 
.
Пусть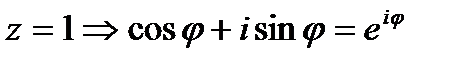 
- тождество Эйлера.
Аналогично комплексно-сопряженные: 
Складывая два эти равенства, получим: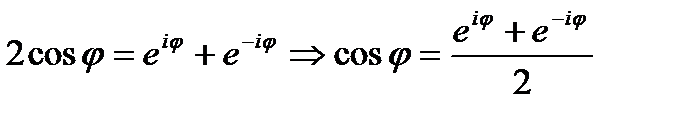 
.
Вычитая эти два равенства, получим: 
Пример. Найти показательную форму комплексного числа 
.
Решение.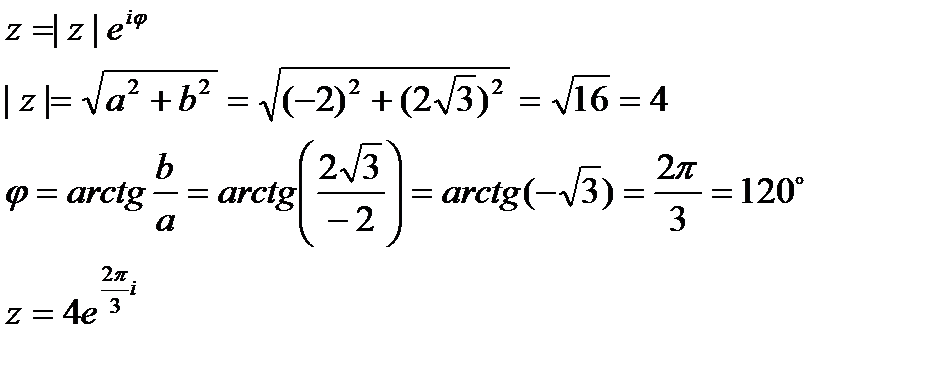 
Задания для выполнения практической работы.
Вариант №1
1.Даны матрицы 
Найти матрицы 
A= 
, B= 
, C=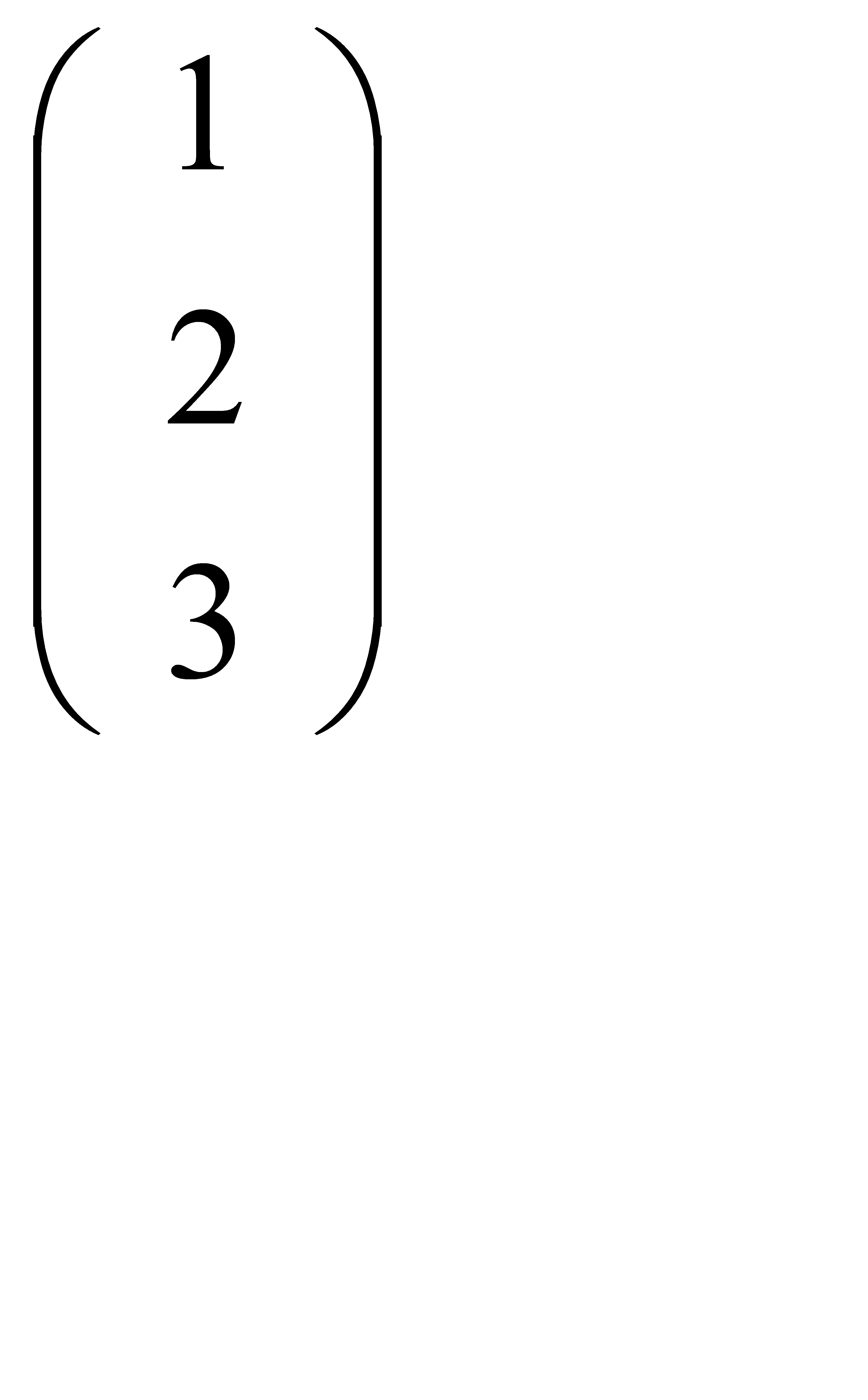 
,
2. Вычислить определитель:
Решить систему уравнений
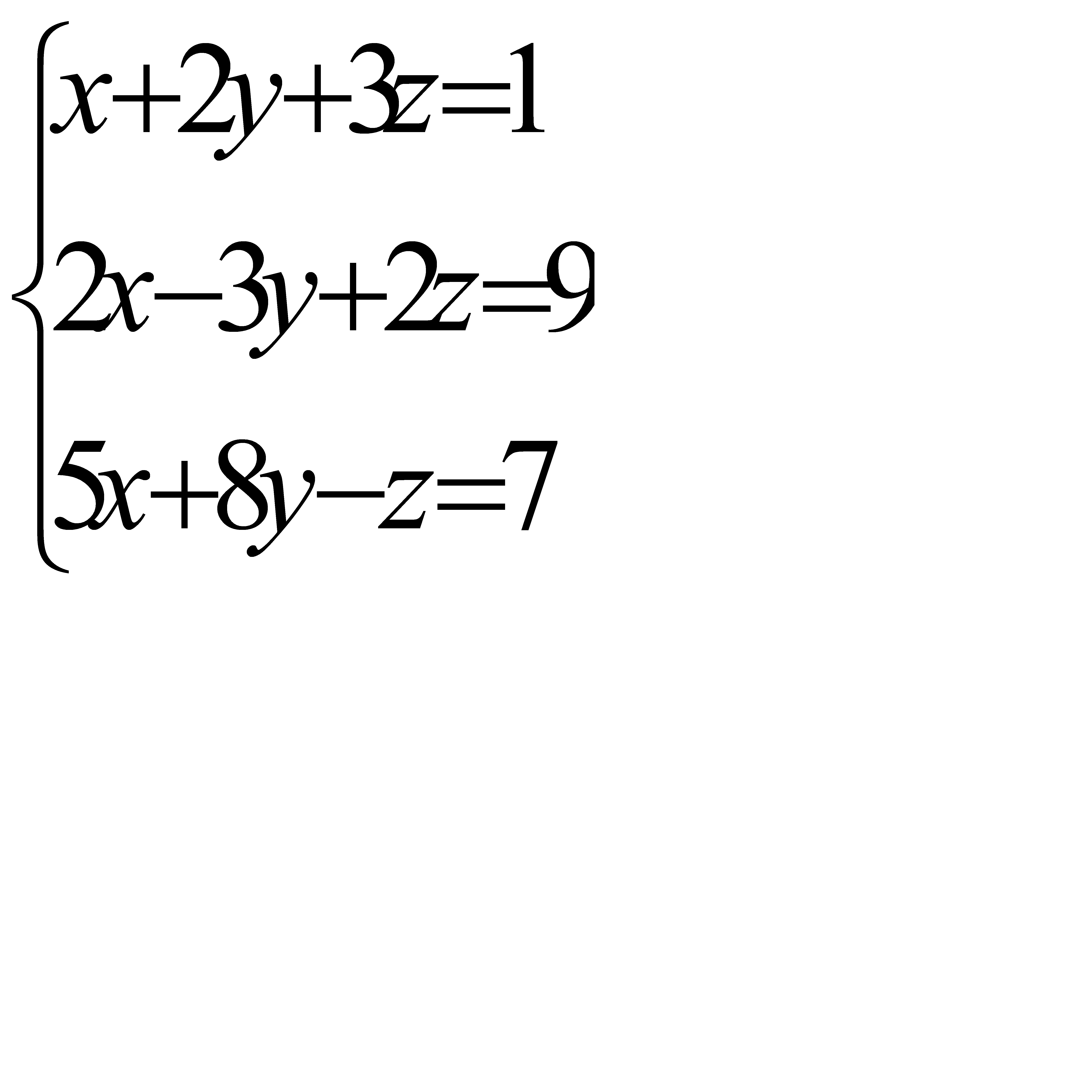
Преобразовать в тригонометрическую форму
5. Выполнить 
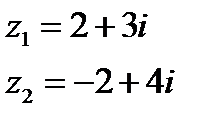
6. Найти
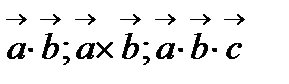если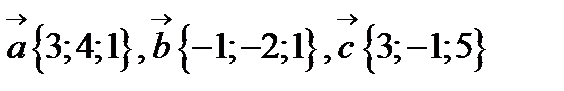 
Вариант №2
1.Даны матрицы
Найти матрицы
A= 
, B= 
, C= 
,
2. Вычислить определитель:
Решить систему уравнений
Преобразовать в тригонометрическую форму
5. Выполнить
6. Найти
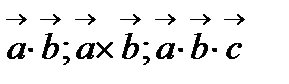если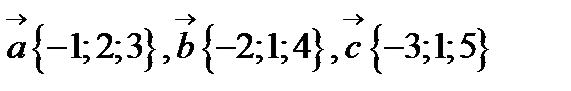 
Вариант № 3
1.Даны матрицы
Найти матрицы
A= 
, B= 
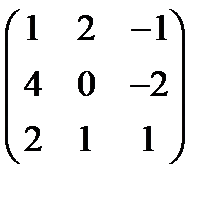, C=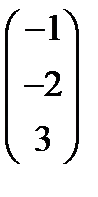 
,
2. Вычислить определитель:
Решить систему уравнений
Преобразовать в тригонометрическую форму
5. Выполнить
6. Найти
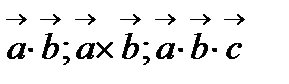если 
Вариант № 4
1.Даны матрицы
Найти матрицы
A= 
, B= 
, C= 
,
2. Вычислить определитель:
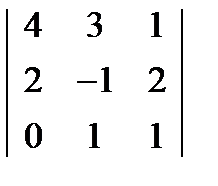
Решить систему уравнений
Преобразовать в тригонометрическую форму
5. Выполнить
6. Найти
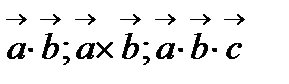если 
Дата добавления: 2020-01-07; просмотров: 121; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!