Энергетический баланс потока идеальной жидкости
Лекция 2
Автор -Трушин А.М.
Уравнение движения идеальной жидкости Эйлера
Выделим в движущейся в поле сил тяжести идеальной (невязкой) жидкости произвольный объём V , ограниченный поверхностью S с единичной внешней нормалью n. Найдём сумму внешних сил, действующих на данный объём.
Поскольку в идеальной жидкости действуют только нормальные напряжения, сила давления, действующая на выделенный объём со стороны окружающей жидкости равна интегралу
(в соответствии с уравнением (1)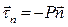 
)
Преобразуя поверхностный интеграл в объёмный, получим
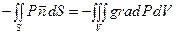
На данный объём действует также внешняя сила тяжести, равная интегралу
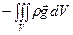
где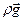 
- сила тяжести единичного объёма.
Таким образом, сумма внешних сил, действующих на объём V, равна интегралу
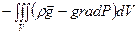
Из этого выражения видно, что на каждый элемент объёма dV действует сила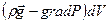 
Из механики известно, что сумма внешних сил, действующих на тело, равна произведению массы тела на его ускорение, следовательно
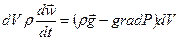
Сократив на величину dV, получим уравнение движения идеальной жидкости Эйлера
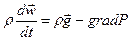(28)
Запишем уравнение движения Эйлера в проекциях на оси координат
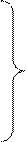
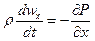
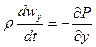(29)
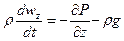
Индивидуальные производные проекций скорости находятся по формуле (21).
|
|
|
Например, для проекции скорости на ось x, получим
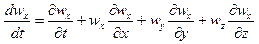
Для несжимаемых невязких жидкостей решение уравнения (28) совместно с уравнением неразрывности (17) позволяет определить четыре неизвестных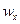 
, 
, 
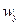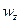,P.
Для изотермических процессов при значительном изменении давления в идеальных сжимаемых жидкостях, при решении аналогичной задачи, кроме уравнений (28) и (15) требуется знание зависимости плотности от давления
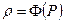(30)
(Жидкости, у которых плотность подчиняется уравнению (32) называются баротронными).
Следует отметить, что случаи, когда необходим учёт сжимаемости при решении таких задач, в химической технологии достаточно редкие.
РАВНОВЕСИЕ ЖИДКОСТИ В ПОЛЕ СИЛЫ ТЯЖЕСТИ.
В покоящейся жидкости (реальной и идеальной) как и в движущейся идеальной жидкости действуют только нормальные напряжения с идентичными свойствами. Поэтому, приравняв скорость нулю в уравнении (28), получим уравнение равновесия Эйлера жидкости в поле сил тяжести
(31)
|
|
|
В проекциях на оси координат уравнение (31) превращается в систему уравнений
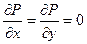
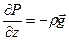(32)
Так как производные давления по x и y равны нулю, для несжимаемой жидкости получим
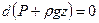
Отсюда получим основное уравнение гидростатики
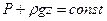(33)
Запишем уравнение (33) для ряда сечений покоящейся жидкости
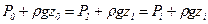(34)
Основное уравнение гидростатики (33) можно также записать в следующей форме
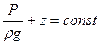(35)
или 
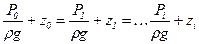(36)
Все составляющие этого уравнения имеют размерность длины и называются напорами или высотами, кроме того, их можно рассматривать как величины удельной (отнесённой к единице веса) потенциальной энергии
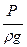– пьезометрический напор (пьезометрическая высота), м.
z – геометрический напор (нивелирная высота), м.
Из уравнения (36) следует, что сумма пьезометрического и геометрического напора для любой точки покоящейся жидкости есть величина постоянная.
|
|
|
Основное уравнение гидростатики служит для определения величин давления, положений раздела фаз в покоящихся жидкостях, а также для определения сил, действующих на дно и стенки аппаратов.
Рассмотрим применение основного уравнения гидростатики на примере простейшего U-образного манометра ( Рис.4), который представляет собой прибор (1) в виде прозрачной трубки, заполненной манометрической жидкостью.
Манометр присоединён к аппарату, содержащему газ, плотность которого пренебрежительно мала по сравнению с плотностью манометрической жидкости.
Уровни жидкости в U-образной трубке z 1 и z 2, причём давление на уровне z 2 атмосферное Р2 = Ратм.
 |
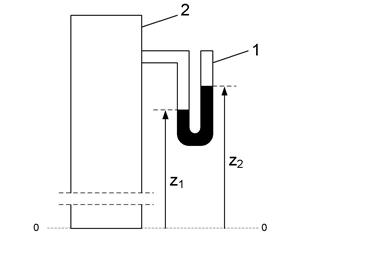Рис.4. Измерение давления U- образным манометром
Запишем уравнение (34) для двух уровней жидкости
Если давление в аппарате выше атмосферного z 2 > z 1, найдём избыточное давление в аппарате по сравнению с атмосферным
Избыточное давление (Ризб) равно разнице между абсолютным давлением в аппарате (Р абс = Р 1) и атмосферным.
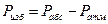(37)
|
|
|
Если давление в аппарате ниже атмосферного, уровень z 1 будет выше уровня z 2, тогда можно записать
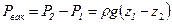
Эта величина (Рвак), называемая разряжением или вакуумом, равна разнице между атмосферным давлением и абсолютным давлением в аппарате.
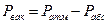(38)
Для сжимаемых жидкостей уравнение интегрируют совместно с уравнением состояния.
В случае баротронных жидкостей 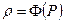получим
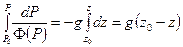(40)
При использовании уравнения (40) следует иметь в виду, что оно даёт существенные расхождения с уравнением (34) только для больших масс (высоких слоёв) сжимаемых жидкостей.
Энергетический баланс потока идеальной жидкости
Рассмотрим стационарное движение физически бесконечно малого объёма идеальной жидкости по линии тока, как известно, совпадающей с траекторией движения этой жидкой частицы. В проекциях на оси координат это движение описывается системой уравнений Эйлера(29).
Умножим правые и левые части системы уравнений (29) на соответствующие проекции элементарного пути пройденного частицей: dx, dy, dz
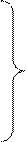
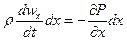
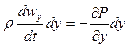(40)
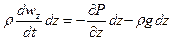
Просуммировав левые и правые части этих уравнений с учетом того, что
, 
, 
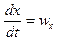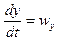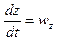получим
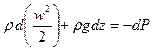(41)
В случае несжимаемой жидкости уравнение (41) упрощается
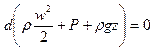, следовательно
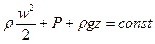(42)
Чаще это уравнение записывают в таком виде
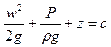(43)
Величина константы с меняется для различных линий тока.
Таким образом, получено уравнение энергетического баланса движения элементарного объёма несжимаемой идеальной жидкости по линии тока, называемое уравнением Бернулли. Согласно этому уравнению сумма удельной (отнесённой к единице веса) кинетической энергии (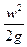 
) и потенциальной энергии давления и положения ( 
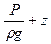) есть величина постоянная для любой точки на линии тока.
Величины удельных энергий также называют напорами, как и в уравнении гидростатики (36) с добавлением скоростного напора.
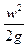- скоростной или динамический напор, м.
Для конечных сечений потока параметры уравнения (43) осредняют по всем линиям тока, т.е. по всему сечению, при этом вместо скорости в точке используют среднюю скорость по поперечному сечению (w ср), поэтому удельная кинетическая энергия, рассчитанная по средней скорости, умножается на поправочный коэффициент a, зависящий от распределения скорости по сечению потока
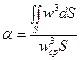(44)
В технических расчётах обычно принимают a =1 по следующим причинам. Величина a при больших скоростях турбулентного течения незначительно превышает 1; при малых скоростях, соответствующих ламинарному движению a = 2. Но поскольку сама величина кинетической энергии в этом случае очень мала по сравнению с величинами потенциальной энергии, приравнивание a единице не вносит существенных погрешностей в расчёты.
При средних скоростях турбулентной области из-за сравнительно малой величины кинетической энергии погрешности также незначительны.
Таким образом, получим уравнение Бернулли для конечных сечений потока несжимаемой идеальной жидкости.
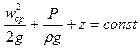
В технических расчётах обычно используют средние по сечению величины скоростей, поэтому принимаем обозначения w ср = w, тогда уравнение Бернулли принимает вид
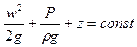(45)
Следовательно, для любых сечений, получим
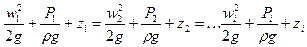(46)
В случае сжимаемой жидкости уравнение (41) записывается в виде:
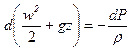(47)
Чтобы решение этого уравнения имело вид аналогичный уравнению Бернулли для идеальной несжимаемой жидкости используют следующую функцию
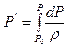
где Ро – значение давления в начальной точке линии тока, или, для конечных сечений, в начальном сечении.
Величину этой функции определяют по известной зависимости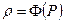
Проинтегрировав уравнение (47), получим уравнение Бернулли для сжимаемой идеальной жидкости
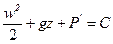(48)
где С – константа.
В технических расчётах уравнение (48) используется очень редко, в случаях очень больших скоростей, сравнимых со скоростью звука, так как при обычных скоростях газа, расчёты проведенные по уравнениям (43) и (48) для сжимаемых и несжимаемых жидкостей не дают существенных расхождений.
Дата добавления: 2019-11-25; просмотров: 403; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!