Операции с векторами и матрицами

Обычная графика матлаб

Построение графиков отрезками прямых

При построении графика значение каждой узловой точки вычисляется с помощью заданных аргументов х. Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера. Процесс построения графиков в декартовой системе координат проводится с помощью команды plot. plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.

» х=[0 12345];

» Y=[sin(x)icos(x)]:

» plot(x.Y)

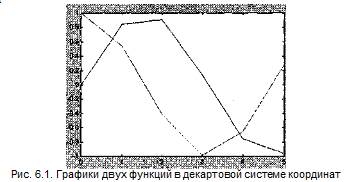
Плавность графика зависит от количества узловых точек. О plot(Y) — строит график у(i), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y). imag(Y)). Во всех других случаях мнимая часть данных игнорируется.

» x=-2*pi:0.02*рт;2*рт:

» y=sin(x)+i*cos(3*x);

» plot(y)

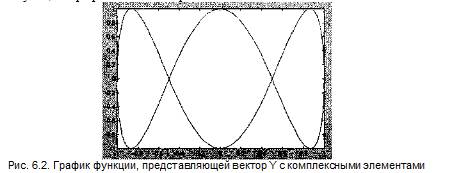
plot(X.Y.S) — аналогична команде plot(X.Y), но тип линии графика можно задавать с помощью строковой константы S.

Графики в логарифмическом масштабе

Если х и у меняются в широких пределах, то оптимальным становится использование логарифмического масштаба. Рассмотрим команды, которые используются в таких случаях.

О loglogL.) — синтаксис команды аналогичен ранее рассмотренному для функции plot(...). Логарифмический масштаб используется для координатных осей X и У. Ниже дан пример применения данной команды:

» х-1ogspace(-1.3);

» loglog(x,exp(x),/х)

» grid on

Графики в полулогарифмическом масштабе

Также для частных случаев существует полулогарифмический масштаб (логарифмический только на одной из осей). При создании таких графиков в команде указывается название оси в логарифмическом масштабе semilogx(„.) и semilogy (...) соответственно. Запись параметров происходит по аналогии с функцией plot(...).

» х=0:0.5:10;

» semi 1 оду(х.ехр(х))

Нетрудно заметить, что при таком масштабе график экспоненциальной функции выродился в прямую линию.

Столбцовые диаграммы

Столбцовые диаграммы широко используются в литературе, посвященной финансам и экономике, а также в математической. bar(х.У) — строит столбцовый график элементов вектора У при этом значения х, должны монотонно возрастать; bar(У) — строит график так же, но

фактически для построения используется вектор х=1 ; barСх. (У .WIDTH) или BAR (У, WIDTH) — аналогична, но со спецификацией ширины столбцов (при WIDTH > 1 столбцы в одной и той же позиции перекрываются). По умолчанию задано WIDTH = 0.8.

Возможно применение этих команд и в следующем виде: bar(.„, 'Спецификация'),

» subplot(2.1.1),

bar(rand(12.3).'stacked'). colormapCcool)

На рис. 6.6 представлен полученный график.

Помимо команды bar(...) существует аналогичная ей по синтаксису команда barh(...), которая строит столбцовые диаграммы с горизонтальным расположением столбцов.

» subplot(2.1.1). barh(rand(5.3),'stacked'). colormap(cool)

Построение гистограмм

При построении гистограмм необходимо вычислить числа попаданий значений элементов вектора Y в М интервалов для выполнения этой работы используют команды: N=hist(Y) для 10 интервалов, выбираемых автоматически; N=hist(Y,M) используется М интервалов; N=hist(Y,X) центры интервалов заданы элементами вектора X; [N,X]=HIST(...) — возвращает числа попаданий в интервалы и данные о центрах интервалов.

. В следующем примере строится гистограмма для 1000 случайных чисел и выводится вектор с данными о числах их попаданий в интервалы, заданные вектором х:

» х=-3:0.2:3:

» y=randn(1000.1):

» hist (у. х)

» h =

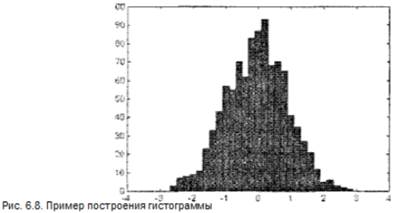
Нетрудно заметить, что распределение случайных чисел близко к нормальному закону. Увеличив их количество, можно наблюдать еще большее соответствие этому закону.

Лестничные графики — команды stairs

Stairs(Y) — строит лестничный график по данным вектора Y; stairs(X.Y) — строит лестничный график по данным вектора Y с координатами х переходов от ступеньки к ступеньке, заданными значениями элементов вектора X; stairs(...,S) — аналогична по действию вышеописанным командам, но строит график линиями, стиль которых задается строками S.

Следующий пример иллюстрирует построение лестничного графика:

» х-0:0.25:10;

» sta1rs(x.xA2):

Отсчеты берутся через равные промежутки по горизонтальной оси. Функция H=stairs(X,Y) возвращает вектор дескрипторов графических объектов. Функция [XX, YY]=stairs(X. Y) сама по себе график не строит, а возвращает векторы XX и YY, которые позволяют построить график с помощью команды plot(XX.YY)

Построение графиков поверхностей

Для построения графиков поверхности используют plot3, аналог команды plot, имеющую формы: plot3(x,y.z) — строит массив точек, представленных векторами х, у и z, соединяя их отрезками прямых; plot3(X. Y.Z), где X, Y и Z — матрицы одинакового размера, строит точки с координатами Х(1.:), Y(1,:) и Z(i.:).

» z(x,y)=xA2+yA2:

» [X.Y]-meshgrid([-3:0.15:3]):

» Z=X.A2+Y.A2;

» plot3(X.Y.Z)

plot3(X, Y.Z.S) — позволяет задать спецификацию стиля линий и точек для графика.

plot3(xl,yl.zl,sl.x2.y2,z2.s2.x3,y3.z3,s3,...) — строит на одном рисунке графики нескольких функций zl(xl ,yl), z2(х2,у2) и т. д. со спецификацией линий и маркеров каждой из них j

» [X,Y]=meshgrid([-3:0.15:3]);

» Z=X.A2+Y.A2:

» plot3(X,Y.Z,'-k'.Y.X.Z.'-k')

В данном случае строятся два графика одной и той же функции с взаимно пер-пендикулярными образующими линиями. Поэтому график имеет вид сетки без окраски ее ячеек (напоминает проволочный каркас фигуры).

Сетчатые 3D-графики с окраской

Наиболее представительными и наглядными являются сетчатые графики с окраской, команды для их создания содержат слово mesh.

mesh(X,Y.Z.C) — выводит в графическое окно сетчатую поверхность Z(X.Y) с цветами узлов поверхности, заданными массивом С;

mesh(X.Y.Z) — аналог предшествующей команды при C=Z( цвет задается высотой по-верхности).

» [X,Y]=meshgnd([-3:0.15:3]);

» Z-X.*2+Y.*2:

» mesh(X.Y.Z)

MATLAB имеет несколько графических функций, возвращающих матричный образ поверхностей. Например, функция peaks(N) возвращает матричный образ поверхности с рядом пиков и впадин.

» z=peaks(25);

» mesh(z).

Сетчатые 3 D-графики с проекциями

Иногда график поверхности полезно объединить с контурным графиком ее проекции на плоскость, расположенным под поверхностью.

Для этого используется команда meshc: meshc(C) — аналогична mesh(..), но помимо графика поверхности дает изображение ее проекции в виде линий равного уровня.

График такого типа дает наилучшее представление об особенностях поверхности.

Построение поверхности столбцами

Еще один тип представления поверхности, когда она строится из многочисленных столбцов, дают команды класса meshz: meshz(L.) — аналогична mesh(L), но строит поверхность как бы в виде столбиков.

Построение поверхности с окраской

Для построения таких поверхностей используются команды класса surf(...): surf (X, Y ,Z,C) — строит цветную параметрическую поверхность по данным матриц X, Y и Z с цветом, задаваемым массивом С; surf(X. Y, Z) — аналогична предшествующей команде, где C=Z, так что цвет задается высотой той или иной ячейки поверхности; surf(x.y.Z) и surf(x.y.Z.C) — векторы х и у заменяют первых два аргумента и должны иметь длины length(x)=n и 1ength(Cy)=m, где [m,n]=size(Z); surf (Z) и surf(Z С) используют х = 1:n и у = 1:m. В этом случае высота Z ; h=surf (...) —строит поверхность и возвращает дескриптор объекта класса surface. Обычно применение интерполяции для окраски придает поверхностям и фигурам более реалистичный вид, но фигуры каркасного вида дают более точные количественные данные о каждой точке.

Построение освещенной поверхности

Для получения графиков поверхности наиболее реалистичного вида(с имитацией освещения) используется команда surfl: surfl (...) — строит график поверхности с подсветкой от источника света; surfl(Z.S)— строит графики поверхности с подсветкой от источника света, положение которого задается вектором S=[Sx,Sy,Sz], а в системе сферических координат — вектором S=[AZ,EL]; surfl(.... 'light') — позволяет задать цвет подсветки; surfl (..., 'cdata') — имитирует эффект отражения; H=surfl (...) — строит поверхность и возвращает дескрипторы поверхности и источников света.

» [X,Y]=meshgrid([-3:0.1:3]);

» Z=sin(X)./СХ.A2+Y.А2+0.3);

» surfKX.Y.Z)

» colormap(gray)

» shading interp » colorbar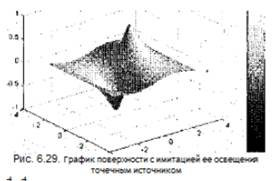

Средства управления подсветкой и обзором фигур

diffuse — задание эффекта диффузионного рассеяния;

lighting — управление подсветкой;

material — имитация свойств рассеивания света различными материалами;

specular — задание эффекта зеркального отражения.

Следующие команды управляют углами просмотра, под которыми рассматривается фигура:

view — задание положения точки просмотра;

viewmtx — задание и вычисление матрицы вращения;

rotate3d — задание поворота трехмерной фигуры.

Построение графиков функций трех переменных

Графики сечений функций трех переменных строит команда slice. Она используется в следующих формах: slice(X,Y,Z,V,Sx,Sy,Sz) — строит плоские сечения объемной фигуры. Массивы X, Y, Z задают координаты и должны быть монотонными и трехмерными с размером MxNxP; sliсе(Х. Y. Z. V, XI. YI.ZI) — строит сечения объемной фигуры по поверхности, определенной массивами XI, YI, ZI; slice(..., 'method') — при построении задается метод интерполяции, который может быть одним из следующих: 'linear', 'cubic' или 'nearest'. По умолчанию используется линейная интерполяция — 'linear'; slice(V.Sx,Sy,Sz) или slice(V,XI,YI,ZI) — подразумевается X=1:N, Y=1 :М, Z=1:P; H=slice(...) — строит сечение и возвращает дескриптор объекта класса surface.

» [X.y.z] - meshgridC-2:.2:2. -2:.25:2, -2:.16:2):

» v - sin(x) .* ехр(-х.А2 - у.А2 - z.A2);

» sTiceCx,y.z,v.t-l-2 .8 2],2,[-2 -.2])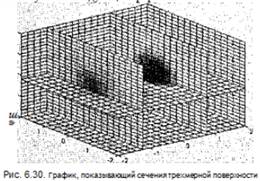

Включение и выключение сетки

При построении графиков в дополнение к разметке осей часто используют масштабную сетку, наличие сетки облегчает количественную оценку координат точек графика. Команды grid позволяют задавать построение сетки или отменять это построение: grid on — добавляет сетку к текущему графику; grid off — отключает сетку; grid-— последовательно производит включение и отключение сетки.

Наложение графиков друг на друга

Для построения графиков с наложением друг на друга используют комаду захвата окна hold on и её формы: hold on — обеспечивает продолжение вывода графиков в текущее окно; hold off — отключает этот режим; hold — работает как переключатель.

Разбиение графического окна

Для того чтобы расположить несколько различных графиков без наложения их друг на друга используются команды subplot, применяемые перед построением графиков: subplot — создает новые подокна; subplot(m.n.p) или subplot(mnp) — разбивает графическое окно на m*n подокон, при этом m — число подокон по горизонтали, n — число подокон по вертикали, р— номер подокна, в которое будет выводиться текущий график; subplot('position'. [left bottom width height]) — создает подокно с заданными нормализованными координатами (в пределах от 0.0 до 1.0); subplot(lll) и cl f reset — удаляют все подокна и возвращают графическое окно в обычное состояние.

» х--5:0.1:5:

subplot(2.2.D,pl<Jt;<x.s1n(x))

Специальная графика

Движение точки на плоскости

Для отображения движения точки по траектории используется команда comet. При этом движущаяся точка напоминает ядро кометы с хвостом. comet (Y) — отображает движение «кометы» по траектории, заданной вектором Y; comet (X.Y) — по траектории, заданной парой векторов Y и X; comet (X.Y.p) — позволяет задавать длину хвоста кометы (отрезка траектории, выделенного цветом) как р*1 ength (Y), где length(Y) - размер вектора Y. а р<1.

По умолчанию р = О.1.18

Следующий пример иллюстрирует применение команды comet:

» Х-0:0.01:15:

» comet(X.sin(X).0.15)

Объекты дескрипторной графики

Центральным понятием дескрипторной графики является графический объект. Имеются следующие типы таких объектов:

root (корень) — первичный объект, соответствующий экрану компьютера;

figure (рисунок) — объект создания графического окна;

uicontrol (элемент управления, определенный пользователем) — объект создания элемента пользовательского интерфейса;

axes (оси) — объект, задающий область расположения графика в окне объекта figure;

ui menu (определенное пользователем меню) — объект создания меню;

uicontextmenu (определенное пользователем контекстное меню) - объект создания контекстного меню;

image (образ) — объект создания растровой графики;

Tine (линия) — объект создания линии;

patch (заплата) — объект создания закрашенных фигур;

rectangle (прямоугольник) - объект создания закрашенных прямоугольников; О surface (поверхность) — объект создания поверхности;

text (текст) — объект создания текстовых надписей;

light (свет) — объект создания эффектов освещенности.

Объекты подчас взаимосвязаны и могут обращаться друг к другу для получения того или иного графического эффекта.

Операции над графическими объектами

К графическим объектам применяется ряд операций:

set — установка свойств (параметров) графического объекта;

get — вывод свойств графического объекта;

reset — восстановить свойства графического объекта по умолчанию;

delete — удалить созданный графический объект;

gсо — возвращает дескриптор текущего графического объекта;

gcbo — возвращает дескриптор объекта, чья функция в данный момент выпол-няется;

gcbf — возвращает дескриптор окна, содержащего объект, функция которого в данный момент выполняется;

drawnow — выполнить очередь задержанных графических команд;

findobj — найти объекты с заданными свойствами;

copyobj — скопировать объект и порожденные им объекты.

Кроме того, имеются три утилиты, связанные с операциями над объектами:

closereq — закрыть окно по запросу;

ishandle — проверить дескриптор на истинность;

newplot — восстановить свойства объекта, измененные nextPlot.

Операторы и функции

Операторы отношения и их функции

Операторы отношения служат для сравнения двух величин, векторов или матриц. Все операторы отношения имеют два операнда, например х и у, и записываются, как показано в табл.

Данные операторы выполняют поэлементное сравнение векторов или матриц одинакового размера и возвращают значение 1 (True), если элементы идентичны, и значение 0 (False) в противном случае. Если операнды — действительные числа, то применение операторов отношения тривиально.

Следует отметить, что операторы <, <=, > и >= при комплексных операндах используют для сравнения только действительные части операндов — мнимые отбрасываются. В то же время операторы == и ~= ведут сравнение с учетом как действительной, так и мнимой частей операндов. Следующие примеры поясняют это положение:

» (2+31)>=(2+i) ans =1

» (2+3i)>(2+i) ans =0

» abs(2+3i)>abs(2+i) ans - 1

» (2+31)—(2+1) ans - 0

» (2+31)~=(2+i) ans =1

Если один из операндов — скаляр, происходит сравнение всех элементов второго операнда-массива со значением этого скаляра:

Таблица 8.2 (продолжение)

Функция Название Оператор Пример

Gt Больше чем > х>у

Le Меньше или равно <= Х<=у

Ge Больше или равно >= Х>=у

м =

-1 о

1 2

» М>=0 ans =

0 1

1 1

В общем случае операторы отношения сравнивают два массива одного размера и выдают результат в виде массива того же размера:

» М>[0 1:10] ans =

0 0

0 1

Таким образом, спектр применения операторов отношения в системе MATLAB шире, чем в обычных языках программирования, поскольку операндами являются не только числа, но и векторы, матрицы и массивы. Возможно применение операторов отношения и к символьным выражениям:

» 'Ь’>'а' ans =

» 'abc'=='abc' ans =

1 1 1

» ' cba'<'abc' ans =

0 0 1

В этом случае символы, входящие в выражения, представляются своими ASCII- кодами. Строки воспринимаются как векторы, содержащие значения кодов. Все это надо учитывать при использовании управляющих структур языка программирования, в которых широко применяются операторы отношения.

Логические операторы

Логические операторы и соответствующие им функции служат для реализации поэлементных логических операций над элементами одинаковых по размеру массивов

Обратите внимание, что аргументами логических операторов могут быть числа и строки. При аргументах-числах логический нуль соответствует числовому нулю, а любое отличное от нуля число воспринимается как логическая единица. Для строк действует уже отмеченное правило — каждый символ строки представляется своим ASCII-кодом.

Элементарные функции

Элементарные функции, пожалуй, наиболее известный класс математических функций. Поэтому, не останавливаясь подробно на их описании, представим набор данных функций, имеющийся в составе системы MATLAB. Функции, перечисленные ниже, сгруппированы по функциональному назначению. В тригонометрических функциях углы измеряются в радианах. Все функции могут использоваться в конструкции вида y=func(x), где func — имя функции. Обычно в такой форме задается информация о функции в системе MATLAB. Мы, однако, будем использовать для функций, возвращающих одиночный результат, более простую форму func(x). Форма [у ,z,...]=func(x,„.) будет использоваться только в тех случаях, когда функция возвращает множественный результат.

Алгебраические и арифметические функции

В системе MATLAB определены следующие алгебраические и арифметические функции:

abs(X) вычисляет модуль каждого числа. Примеры:

abs(-5) = 5 abs(3+4i) - 5 » abs([l -2 i 31 2+31]) ans -

1.0 2.0000 1.0000 3.0000 3.6056

exp(X) — возвращает экспоненту для каждого элемента X.

Примеры:

» ехр([1 2 3]) ans -

2.7183 7.3891 20.0855

» exp(2+3i) ans =

-7.3151 + 1.0427 i

factor(n) — возвращает вектор-строку, содержащую простые множители числа n. Для массивов эта функция неприменима. Пример:

f = factor(221) f -

13 17

log (X) — возвращает натуральный логарифм элементов массива X. Для комп-лексного или отрицательного г, где г = х + y*i, вычисляется комплексный ло-гарифм в виде log(z) = logfabs(z)) + i*atan2(y,x). Функция логарифма вычисляется для каждого элемента массива. Область определения функции включает комплексные и отрицательные числа, что способно привести к непредвиденным результатам при некорректном использовании. Пример:

» Х-[1.2 3.34 5 2.3];

» 1оg(Х)

ans -

0.1823 1.2060 1.6094 0.8329

1оg2(Х) — возвращает логарифм по основанию 2 элементов массива X;

[F.E] = 1оg2(Х) — возвращает массив действительных значений F и массив целых чисел

Е. Элементы массива F обычно лежат в диапазоне 0.5 J abs(F) < 1. Для действительных X возвращаемые массивы F удовлетворяют уравнению вида X = F.*2.E. Для нулевых значений X возвращаются F = 0 и Е = 0.

Пример:

» Х=[2 4.678 5:0.987 1 3]:

» [F.E] = 1 og2(X)

F =

0.5000 0.5847 0.6250 0.9870 0.5000 0.7500 Е =

2 3 3

0 1 2

sqrt(A) — возвращает квадратный корень каждого элемента массива X. Для отрицательных и комплексных элементов X функция sqrt(X) вычисляет комплексный результат.

Пример:

» А=[25 21.23 55.8 3];

» sqrt(A) ans =

5.0 4.6076 7.4699 1.7321

Тригонометрические и обратные им функции

Тригонометрические функции в MATLAB записываются: sin, cos, tan ,cot, csc, sec для функций с приставкой arc прибавляется приставка а, для гиперболической окончание h, запись для каждой функции аналогична:

acos(X) — возвращает арккосинус для каждого элемента X. Для действительных значений X в области [-1, 1] acos(X) возвращает действительное значение из диапазона диапазона [0, р], для действительных значений X вне области [-1, 1 ] acos(X) возвращает комплексное число.

Примеры:

»Y = acos (0.5)

Y =

1.0472

» acos([0.5 1 2]) ans =

1.472 0 0 + 1.3170

Функции комплексного аргумента

Для работы с комплексными числами и данными в MATLAB используются сле-дующие функции:

imag(Z) — возвращает мнимые части всех элементов массива Z. Пример:

» Z=[l+i, 3+2i, 2+3i]:

» imag(Z) ans =

1 2 3

real (Z) — возвращает вещественные части всех элементов комплексного массива Z. Пример:

» Z=[l+i, 3+2i. 2+3i];

» real(Z) ans =

13 2

conj(Z) — возвращает число, комплексно-сопряженное аргументу Z. Если Z комплексное, то conj(Z) = real (Z) - i *imag(Z). Пример:

» conj(2+3i) ans =

2.0 - 3.OOOOi

Операции с векторами и матрицами

Создание единичной матрицы

Для создания единичной матрицы (она обычно обозначается как Е) служит функция eye:

еуе(n) — возвращает единичную матрицу размера n*n;

eye(m.n) или еуе([m n]) — возвращают матрицу размера m*n с единицами по диагонали и нулями в остальных ячейках;

eye(size(A)) — возвращает единичную матрицу того же размера, что и А.

Единичная матрица не определена для многомерных массивов. Так, функция у = еуе( [2.3.4]) при попытке ее вычисления приведет к ошибке.

Пример использования функции eye:

» t-eye(4,5) t =

Создание матрицы с единичными элементами

Для создания матриц, все элементы которых — единицы, используется функция ones, а когда все элементы — нули zeros с аналогичными формами и методами использования.

Создание линейного массива равноотстоящих точек

Функция 1 inspace формирует линейный массив равноотстоящих узлов. Это подобно оператору

:, но дает прямой контроль над числом точек. Применяется в следующих формах:

О linspace(a.b) — возвращает линейный массив из 100 точек, равномерно рас-пределенных между а и Ь;

О linspace(a.b.n) — генерирует п точек, равномерно распределенных в интервале от а до b.

Пример:

» М-1 inspace(4.20.14)

М -

Columns 1 through 7

4.0 5.2308 6.4615 7.6923 8.9231 10.153811.3846

Columns 8 through 14 '

12.615413.846215.076916.307717.538518.769220.0000

Для вектора равноотстоящих в логарифмическом масштабе точек вместо lin записывается log

logspace(a,b) — возвращает вектор-строку из 50 равноотстоящих в логарифмическом масштабе точек между декадами 10° и 10*;

logspace(a.b.n) — возвращает п точек между декадами 10“ и 104;

О logspace (a, pi) — возвращает точки в интервале между 10° и я. Эта функция очень полезна в цифровой обработке сигналов.

Все аргументы функции logspace должны быть скалярными величинами.

Конкатенация матриц

Конкатенацией называют объединение массивов, которое реализует следующая функция.

О С = cat (dim. А, В) — объединяет массивы А и В в соответствии со спецификацией размерности dim и возвращает объединенный массив; dim = 1 — горизонтальная конкатенация, dim = 2 — вертикальная, dim = 3 — многомерный массив размерности Зит. д.;

О С = cat (dim. А1 .А2.АЗ.А4,...) объединяет все входные массивы (Al, А2, АЗ, А4 и т. д.) в соответствии со спецификацией размерности dim и возвращает объединенный массив;

О cat(2,А.В) — это то же самое, что и [А.В], a cat(1,А, В) — то же самое, что и [А;В]. При записи cat (dim, С(:)) или cat (dim, С. field) эта функция применима к массивам ячеек или структур, содержащим численные матрицы. Пример:

» А =[2,4:3.5] :В=[8.7:9.0]:C=cat(1.А,В)

С =

2 4

3 5

8 7

9 О

Перестановки элементов матриц

Для перестановок элементов матриц служат следующие функции:

В = fliplr(A) — зеркально переставляет столбцы матрицы А относительно вер-тикальной оси.

Пример:

» F=[l.2.3:5.45.3]

F =

1 2 3

4 45 3

» fliplr(F) ans =

2 2 1

2 45 5

В = flipud(A) — зеркально переставляет строки матрицы А относительно гори-зонтальной оси.

Пример:

perms(v) — возвращает матрицу Р, которая содержит все возможные перестановки элементов вектора v, каждая перестановка в отдельной строке. Матрица Р содержит n строк и n столбцов.

Вычисление произведений

Несколько простых функций служат для перемножения элементов массивов:

prod(A) — возвращает произведение элементов массива, если А — вектор, или вектор-строку, содержащую произведения элементов каждого столбца, если А — матрица;

prod(A.dim) — возвращает матрицу (массив размерности два) с произведением элементов массива А по столбцам (dim=l), по строкам^т=2), по иным размерностям в зависимости от значения скаляра dim.

Пример:

» А=[1 2 3 4: 2 4 5 7: 6 8 3 4]

А =

12 3 4

2 4 5 7

5 8 3 4

» B=prod(A)

В =

12 64 45 112

cumprod(A) — возвращает произведение с накоплением

cumprod(A.dim) — возвращает произведение с накоплением элементов по строкам или столбцам матрицы в зависимости от значения скаляра dim. Например, cumprod(А. 1) дает прирост первому индексу (номеру строки), таким образом вы-полняя умножение по столбцам матрицы А.

Примеры:

» А-[1 2 3; 4 5 6; 7 8 9]

А -

1 2 3

4 5 6

6 8 9.

» В ” cumprod(A)

В -

cross(U. V) — возвращает векторное произведение векторов U и V в трехмерном пространстве, т. е. W=UxV. U и V — обязательно векторы с тремя элементами; О cross(U.V,dim) — возвращает векторное произведение U и V по размерности, определенной скаляром dim. U и V — многомерные массивы, которые должны иметь одну и ту же размерность, причем размер векторов в каждой размерности size(U.dim) и size(V.dim) должен быть равен 3.

Пример:

» а = [6 5 3]; b - [1 7 б]:с = cross(а,Ь) с =

9 -33 37

Суммирование элементов

Определены следующие функции суммирования элементов массивов:

sum(A) — возвращает сумму элементов массива, если А — вектор, или вектор- строку, содержащую сумму элементов каждого столбца, если А — матрица;

sum(A.dim) — возвращает сумму элементов массива по столбцам (dim=l), строкам (dim-2) или иным размерностям в зависимости от значения скаляра dim.

cumsum(A) — возвращает вектор, содержащий результаты суммирования с накоплением элементов вектора А. Если А — матрица, cumsum(A) возвращает матрицу того же размера, что и А, содержащую суммирование с накоплением для каждого столбца матрицы А;

cumsum(A.dim) — выполняет суммирование с накоплением элементов по размер-ности, определенной скаляром dim. Например, cumsum(A.l) выполняет сумми-рование по столбцам.

Пример: » A=magic(4) А = 16 2 3 13

5 11 10 8

9 7 6 12

4 14 15 1

» В = sum(A) В =

34 34 34 34

Функции формирования матриц

Для создания матриц, состоящих из других матриц, используются следующие функции:

repmat(A,m,n) — возвращает матрицу В, состоящую из гпхп копий матрицы А (т. е.

в матрице ггхп каждый элемент заменяется на копию матрицы А);

repmat(A.n) — формирует матрицу, состоящую из пхп копий матрицы А;

repmat(A,[m п]) — дает тот же результат, что и repmat(A,m,n);

repmat(A,[m п р...]) — возвращает многомерный массив (шхпхр...), состоящий из копий многомерного массива или матрицы А;

repmat (А, m, п) — когда А — скаляр, возвращает матрицу размера mxn со значения-ми элементов, заданных А. Это делается намного быстрее, чем A*ones(m,n).

Поворот матриц

Следующая функция обеспечивает поворот матрицы (по расположению элементов): О rot90(A) — осуществляет поворот матрицы А на 90° против часовой стрелки; О rot90(A.k) — осуществляет поворот матрицы А на величину 90*к градусов, где к — целое число.

Выделение треугольных частей матриц

Lkz выделениz треугольных частей матриц:

tril(X) — возвращает матрицу, все элементы которой выше главной диагонали X заменены нулями, неизменными остаются лишь элементы нижней треугольной части, включая элементы главной диагонали;

tril(X.k) — возвращает неизменной нижнюю треугольную часть матрицы X начиная с k-й диагонали. При к=0 это главная диагональ, при к>0 — одна из верхних диагоналей, при к<0 — одна из нижних диагоналей.

Пример:

» М-[3.1.4:8.3.2:8.1.1]

8 3 2

7 1 1

» tril(M) ans =

3 0 0

8 3 0

8 1 1

triu(Х) — возвращает неизменной верхнюю треугольную часть матрицы X включая элементы главной диагонали, и заменяет нулями остальные элементы;

triu(X.k) — возвращает неизменной верхнюю треугольную часть матрицы X начиная с &-й диагонали. При к=0 — это главная диагональ, при к>0 — одна из верхних диагоналей, при к<0 — одна из нижних диагоналей.

Матричные функции

Весьма представителен в MATLAB набор матричных функций. Они перечислены ниже.

ехрт(Х) — возвращает ех от матрицы X. Комплексный результат получается, если X имеет неположительные собственные значения. Пример:

» S-[l.0.3:1.3.1:4.0.0]

S =

1 0 3

1 3 1

4 0 0

» a=expm(S) а =

31.2203 0

38.965920.0855

31.1705 0

funm( X,(Pfunct 1 on)1— возвращает любую функцию от квадратной матрицы X, если правильно ввести имя, составленное из латинских букв. Команды funm(X ,ехр). funm(X,sqrt). funm(X,log) и ехрm(Х) ,sqrtm(x) ,1 ogm(X) вычисляют соответственно одинаковые функции, но используют разные алгоритмы. Однако предпочтительнее использовать expm(X), sqrtm(x).logm(X);

Дата добавления: 2019-11-25; просмотров: 268; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!