В сфере развития познавательных универсальных учебных действий
Выпускник научится:
· основам реализации проектно-исследовательской деятельности;
· проводить наблюдение и эксперимент под руководством учителя;
· осуществлять расширенный поиск информации с использованием ресурсов библиотек и сети Интернет;
· создавать и преобразовывать модели и схемы для решения задач;
· осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
· давать определение понятиям;
· устанавливать причинно-следственные связи;
· осуществлять логическую операцию установления родовидовых отношений;
· обобщать понятия — осуществлять логическую операцию перехода от видовых признаков к родовому понятию, от понятия с меньшим объёмом к понятию с большим объёмом;
· осуществлять сравнение, сериацию и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций;
· строить классификацию на основе отрицания;
· строить логическое рассуждение, включающее установление причинно-следственных связей;
· объяснять явления, процессы, связи и отношения, выявляемые в ходе исследования;
· основам ознакомительного, изучающего, усваивающего и поискового чтения;
· структурировать тексты, включая умение выделять главное и второстепенное, главную идею текста, выстраивать последовательность описываемых событий;
· работать с метафорами — понимать переносный смысл выражений, понимать и употреблять обороты речи, построенные на скрытом уподоблении, образном сближении слов.
|
|
|
Выпускник получит возможность научиться:
· основам рефлексивного чтения;
· ставить проблему, аргументировать её актуальность;
· самостоятельно проводить исследование на основе применения методов наблюдения и эксперимента;
· выдвигать гипотезы о связях и закономерностях событий, процессов, объектов;
· организовывать исследование с целью проверки гипотез;
· делать умозаключения (индуктивное и по аналогии) и выводы на основе аргументации.
В сфере развития коммуникативных универсальных учебных действий
Выпускник научится:
· учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;
· формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности;
· устанавливать и сравнивать разные точки зрения, прежде чем принимать решения и делать выбор;
· аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом;
· задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с партнёром;
|
|
|
· осуществлять взаимный контроль и оказывать в сотрудничестве необходимую взаимопомощь;
· адекватно использовать речь для планирования и регуляции своей деятельности, решения различных коммуникативных задач;
· владеть устной и письменной речью;
· строить монологическое контекстное высказывание;
· организовывать и планировать учебное сотрудничество с учителем и сверстниками, определять цели и функции участников, способы взаимодействия;
· планировать общие способы работы;
· осуществлять контроль, коррекцию, оценку действий партнёра, уметь убеждать;
· работать в группе — устанавливать рабочие отношения, эффективно сотрудничать и способствовать продуктивной кооперации;
· интегрироваться в группу сверстников и строить продуктивное взаимодействие со сверстниками и взрослыми;
· основам коммуникативной рефлексии;
· использовать адекватные языковые средства для отображения своих чувств, мыслей, мотивов и потребностей;
· отображать в речи (описание, объяснение) содержание совершаемых действий как в форме громкой социализированной речи, так и в форме внутренней речи.
|
|
|
Выпускник получит возможность научиться:
· учитывать и координировать отличные от собственной позиции других людей в сотрудничестве;
· учитывать разные мнения и интересы и обосновывать собственную позицию;
· понимать относительность мнений и подходов к решению проблемы;
· продуктивно разрешать конфликты на основе учёта интересов и позиций всех участников, поиска и оценки альтернативных способов разрешения конфликтов; договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов;
· брать на себя инициативу в организации совместного действия (деловое лидерство);
· оказывать поддержку и содействие тем, от кого зависит достижение цели в совместной деятельности;
· осуществлять коммуникативную рефлексию как осознание оснований собственных действий и действий партнёра;
· в процессе коммуникации достаточно точно, последовательно и полно передавать партнёру необходимую информацию как ориентир для построения действия;
· вступать в диалог, а также участвовать в коллективном обсуждении проблем, участвовать в дискуссии и аргументировать свою позицию, владеть монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка;
|
|
|
· следовать морально-этическим и психологическим принципам общения и сотрудничества на основе уважительного отношения к партнёрам, внимания к личности другого, адекватного межличностного восприятия, готовности адекватно реагировать на нужды других, в частности оказывать помощь и эмоциональную поддержку партнёрам в процессе достижения общей цели совместной деятельности;
· устраивать эффективные групповые обсуждения и обеспечивать обмен знаниями между членами группы для принятия эффективных совместных решений;
· в совместной деятельности чётко формулировать цели группы и позволять её участникам проявлять собственную энергию для достижения этих целей.
Регулятивные
· Самостоятельно определять цели, задавать параметры и критерии, по которым можно определить, что цель достигнута;
· Оценивать последствия достижения поставленной цели для себя и окружающих людей;
· Ставить и формулировать собственные задачи в образовательной деятельности и жизненных ситуациях;
· Оценивать ресурсы, в том числе время и другие нематериальные ресурсы, необходимые для достижения поставленной ранее цели;
· Выбирать путь достижения цели, планировать решение поставленных задач, оптимизируя материальные и нематериальные затраты;
· Организовывать эффективный поиск ресурсов, необходимых для достижения поставленной цели;
· Сопоставлять полученный результат деятельности с поставленной заранее целью.
Познавательные
· Искать и находить обобщенные способы решения задач, в том числе осуществлять развернутый информационный поиск и ставить на его основе новые (учебные и познавательные) задачи;
· Критически оценивать и интерпретировать информацию с разных позиций, распознавать и фиксировать противоречия в информационных источниках;
· Использовать различные модельно – схематические средства для представления существенных связей и отношений, а также противоречий, выявленных в информационных источниках;
· Использовать различные модельно – схематические средства для представления существенных связей и отношений, а также противоречий, выявленных в информационных источниках;
· Находить и приводить критические аргументы в отношении действий и суждений другого; спокойно и разумно относиться к критическим замечаниям в отношении собственного суждения, рассматривать их как ресурс собственного развития;
· Выходить за рамки учебного предмета и осуществлять целенаправленный поиск возможности широкого переноса средств и способов действия;
· Выстраивать индивидуальную образовательную траекторию, учитывая ограничения со стороны других участников и ресурсные ограничения;
· Менять и удерживать разные позиции в познавательной деятельности.
Коммуникативные
· Осуществлять деловую коммуникацию как со сверстниками, так и со взрослыми (как внутри образовательной организации, так и за ее пределами), подбирать партнеров для деловой коммуникации исходя из соображений результативности взаимодействия, а не личных симпатий;
· При осуществлении групповой работы быть как руководителем, так и членом команды в разных ролях (генератор идей, критик, исполнитель, выступающий, эксперт и т.д.);
· Координировать и выполнять работу в условиях реального, виртуального и комбинированного взаимодействия;
· Развернуто, логично и точно излагать свою точку зрения с использованием адекватных (устных и письменных) языковых средств;
· Распознавать конфликтные ситуации и предотвращать конфликты до их активной фазы, выстраивать деловую и образовательную коммуникацию, избегая личных оценочных суждений.
Предметные результаты:
· освоенные обучающимися в ходе изучения учебного предмета умения, специфические для данной предметной области, виды деятельности по получению нового знания в рамках учебного предмета, его преобразованию и применению в учебных, учебно-проектных и социально-проектных ситуациях;
· формирование научного типа мышления, научных представлений о ключевых теориях, типах и видах отношений, владение научной терминологией, ключевыми понятиями, методами и приемами;
· профильного уровня ориентированы на подготовку к последующему профессиональному образованию, развитие индивидуальных способностей учащихся путем более глубокого, чем это предусматривается базовым курсом, освоением основ наук, систематических знаний и способов действий, присущих данному учебному предмету.
Базовый уровень
· сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;
· сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
· владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
· владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
· сформированность представлений об основных понятиях, идеях и методах математического анализа;
· владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
· сформированность представлений о процессах и явлениях, имеющих вероятностный характер, остатистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин.
Профильный уровень
· сформированность представлений о социальных, культурных и исторических факторах становления математики;
· сформированность основ логического, алгоритмического и математического мышления;
· сформированность умений применять полученные знания при решении различных задач;
· сформированность представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления;
· сформированность представлений о необходимости доказательств при обосновании математических утверждений и роли аксиоматики в проведении дедуктивных рассуждений;
· сформированность понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач;
· сформированность умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат;
· сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
· владение умениями составления вероятностных моделей по условию задачи и вычисления вероятности наступления событий, в том числе с применением формул комбинаторики и основных теорем теории вероятностей; исследования случайных величин по их распределению.
Содержание курса учебного предмета «Математика»
10 класс
Геометрия на плоскости
Свойства биссектрисы угла треугольника. Решение треугольников. Вычисление биссектрис, медиан, высот, радиусов вписанной и описанной окружностей. Формулы площади треугольника: формула Герона, выражения площади треугольника через радиус вписанной и описанной окружностей. Окружность. Четырехугольник.
Тригонометрия.
Синус и косинус угла и числа.
Понятие угла и его меры. Радианная мера угла. Определение синусаи косинуса угла и числа. Основное тригонометрическое тождество для синуса и косинуса. Понятия арксинуса, арккосинуса.
Тангенс и котангенс угла и числа.
Определение тангенса икотангенса угла. Основные тригонометрические тождества для тангенса и котангенса. Понятие арктангенса и арккотангенса.
Введение в стереометрию
Основные понятия стереометрии (точка, прямая, плоскость, пространство). Понятие об аксиоматическом способе построения геометрии.
Тригонометрические функции числового аргумента
Тригонометрические функции, их свойства и графики, периодичность, основной период.
Параллельность прямых и плоскостей
Параллельность прямых, прямой и плоскости. Взаимное расположение прямых в пространстве. Угол между двумя прямыми. Параллельность плоскостей. Тетраэдр и параллелепипед.
Параллельное проектирование. Ортогональное проектирование. Площадь ортогональной проекции многоугольника. Изображение пространственных фигур. Центральное проектирование.
Формулы сложения
Синус, косинус и тангенс суммы и разности двух аргументов. Формулы приведения. Синус и косинус двойного аргумента. Формулы половинного аргумента. Преобразование суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразование тригонометрических выражений.
Тригонометрические уравнения и неравенства
Решение простейших тригонометрических уравнений. Тригонометрические уравнения, сводящиеся к простейшим заменой неизвестного. Применение основных тригонометрических формул для решения уравнений. Однородные уравнения. Решение тригонометрических неравенств. Неравенства, сводящиеся к простейшим заменой неизвестного. Введение вспомогательного угла. Замена неизвестного.
Перпендикулярность прямой и плоскости
Перпендикулярность плоскостей, признаки и свойства. Перпендикулярность прямой и плоскости. Двугранный угол, линейный угол двугранного угла. Перпендикуляр и наклонные. Угол между прямой и плоскостью.
Расстояния от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми.
Действительные числа
Множества чисел и операции над множествами чисел. Метод математической индукции. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Доказательство неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел.
Делимость целых чисел. Деление с остатком. Сравнения. Решение задач с целочисленными неизвестным.
Многогранники
Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники.
Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб.
Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида.
Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире.
Сечения многогранника. Построение сечений.
Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Рациональные уравнения и неравенства
Рациональные выражения. Многочлены от нескольких переменных, симметрические многочлены. Формула бинома Ньютона, свойства биноминальных коэффициентов, треугольник Паскаля. Формулы сокращённого умножения для старших степеней.
Многочлены от одной переменной. Делимость многочленов. Деление многочленов с остатком. Рациональные корни многочленов с целыми коэффициентами. Теорема Безу. Число корней многочлена. Решение целых алгебраических уравнений.
Рациональные уравнения и неравенства, системы рациональных неравенств с одной переменной.
Корень степени n
Понятие функции, ее области определения и множества значений. Функция y = xn, где n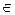 
N, ее свойства и график. Понятие корня степени n>1 и его свойства, понятие арифметического корня.
Степень положительного числа
Понятие степени с рациональным показателем, свойства степени с рациональным показателем. Понятие о пределе последовательности. Существование предела монотонной и ограниченной последовательности. Теоремы о пределах последовательностей. Переход к пределам в неравенствах. Длина окружности и площадь круга как пределы последовательностей. Ряды,бесконечная геометрическая прогрессия и ее сумма. Число e. Понятие степени с действительным показателем. Показательная функция, ее свойства и график.
Логарифмы
Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени, переход к новому основанию. Десятичный и натуральный логарифмы. Преобразование выражений, содержащих логарифмы.
Логарифмическая функция, ее свойства и график.
Простейшие показательные и логарифмические уравнения и неравенства и методы их решения
Показательные и логарифмические уравнения и неравенства и методы их решения.
Вероятность событий. Частота.
Табличное и графическое представление данных. Числовые характеристики рядов данных.
Поочерёдный и одновременный выбор нескольких элементов из конечного множества.
Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события.
11 класс
Функции и их графики
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой у = х.Растяжение и сжатие вдоль осей координат.
Понятие о непрерывности функции. Основные теоремы о непрерывных функциях.
Понятие о пределе функции в точке. Поведение функций на бесконечности. Асимптоты. Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций.
Сложная функция (композиция функций). Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной. Обратные тригонометрические функции, их свойства и графики.
Векторы
Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Координаты вектора. Компланарные векторы. Разложение по трем некомпланарным векторам.
Метод координат в пространстве
Декартовы координаты в пространстве. Формула расстояния между двумя точками. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости.
Угол между векторами. Скалярное произведение векторов. Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам
Производная и ее применение
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения и частного. Производные основных элементарных функций. Производные сложной и обратной функций. Вторая производная. Применение производной к исследованию функций и построению графиков. Использование производных при решении уравнений и неравенств, при решении текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений.
Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Нахождение скорости для процесса, заданного формулой или графиком. Вторая производная и ее физический смысл.
Тела и поверхности вращения
Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию.
Шар и сфера, их сечения. Эллипс, гипербола, парабола как сечения конуса. Касательная плоскость к сфере. Сфера, вписанная в многогранник. Сфера, описанная около многогранника.
Цилиндрические и конические поверхности
Первообразная и интеграл
Площадь криволинейной трапеции. Понятие об определенном интеграле. Первообразная. Первообразные элементарных функций. Правила вычисления первообразных. Формула Ньютона-Лейбница. Примеры применения интеграла в физике и геометрии.
Объемы тел и площади их поверхностей
Понятие об объеме тела. Отношение объемов подобных тел.
Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.
Уравнения и неравенства
Многочлены от двух переменных. Многочлены от нескольких переменных, симметрические многочлены.
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение иррациональных неравенств. Решение систем уравнений с двумя неизвестными простейших типов. Решение систем неравенств с одной переменной.
Доказательства неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел. Переход к пределам в неравенствах.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
Комплексные числа
Комплексные числа. Геометрическая интерпретация комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия над комплексными числами в разных формах записи. Комплексно сопряженные числа. Основная теорема алгебры.
Тематическое планирование
Класс
I вариант: 4 часа в неделю, всего 140 часов
II вариант: 8 часов в неделю, всего 280 часов
III вариант: 9 часов в неделю, всего 315 часов
10 а - I вариант 10 в - II вариант 10 б - III вариант
Класс
I вариант: 4 часа в неделю, всего 132 часов
(по плану на 19-20 гг. 33 недели )
II - III вариант: 9 часов в неделю,всего 297 часов
(по плану на 19-20 гг. 33 недели)
11 а - I вариант 11 б - II вариант 11 в - III вариант
10 класс
| Содержание учебного материала | Количество часов | ||
| I | II | III | |
| Повторение курса алгебры | 9 | 11 | 13 |
| Некоторые сведения из планиметрии | 4 | 5 | 6 |
| Углы и отрезки, связанные с окружностью | 1 | 1 | 2 |
| Решение треугольников | 2 | 2 | 2 |
| Четырехугольник | 1 | 2 | 2 |
| Контрольная работа по теме «Повторение курса алгебры» | 1 | 1 | 1 |
| Синус и косинус угла | 5 | 11 | 15 |
| Понятие угла | 2 | 2 | |
| Радианная мера угла | 1 | 2 | 2 |
| Определение синуса и косинуса угла | 1 | 2 | 2 |
| Основные формулы для синуса и косинуса | 1 | 3 | 3 |
| Арксинус | 1 | 1 | 3 |
| Арккосинус | 1 | 1 | 3 |
| Тангенс и котангенс угла | 4 | 6 | 9 |
| Определение тангенса и котангенса угла | 1 | 1 | 2 |
| Основные формулы для тангенса и котангенса | 1 | 2 | 3 |
| Арктангенс | 1 | 1 | 1 |
| Арккотангенс | 1 | 1 | 1 |
| Формулы для арктангенса и арккотангенса | 1 | 2 | |
| Введение в стереометрию | 3 | 4 | 6 |
| Предмет стереометрии. Основные понятия и аксиомы стереометрии | 1 | 2 | 3 |
| Первые следствия из аксиом, теорем. | 2 | 2 | 3 |
| Тригонометрические функции числового аргумента | 3 | 6 | 8 |
| Функция у= sinα, у=cosα | 1 | 3 | 4 |
| Функция у=tgα, у=ctgα | 1 | 2 | 3 |
| Контрольная работа по теме «Тригонометрические функции» | 1 | 1 | 1 |
| Параллельность прямых и плоскостей | 6 | 10 | 12 |
| Параллельность прямых, прямой и плоскости | 1 | 1 | 2 |
| Взаимное расположение прямых в пространстве. Угол между прямыми | 1 | 2 | 3 |
| Параллельность плоскостей | 1 | 1 | 1 |
| Тетраэдр и параллелепипед | 1 | 2 | 2 |
| Построение сечений тетраэдра и параллелепипеда | 2 | 2 | |
| Итоговый урок по теме | 1 | 1 | 1 |
| Контрольная работа по теме «Параллельность прямых и плоскостей» | 1 | 1 | 1 |
| Формулы сложения | 7 | 15 | 15 |
| Косинус разности и косинус суммы двух углов | 1 | 2 | 2 |
| Формулы для дополнительных углов | 2 | 2 | |
| Синус суммы и синус разности двух углов | 1 | 2 | 2 |
| Сумма и разность синусов и косинусов | 1 | 2 | 2 |
| Формулы для двойных и половинных углов | 1 | 2 | 2 |
| Произведение синусов и косинусов | 1 | 2 | 2 |
| Формулы для тангенсов | 1 | 2 | 2 |
| Контрольная работа по теме «Формулы сложения. Тригонометрические функции» | 1 | 1 | 1 |
| Тригонометрические уравнения и неравенства | 7 | 15 | 18 |
| Простейшие тригонометрические уравнения | 1 | 2 | 2 |
| Уравнения, сводящиеся к простейшим заменой неизвестного | 1 | 2 | 2 |
| Применение основных тригонометрических формул для решения уравнений | 1 | 2 | 2 |
| Однородные уравнения | 1 | 2 | 2 |
| Простейшие неравенства для синуса и косинуса | 1 | 1 | 2 |
| Простейшие неравенства для тангенса и котангенса | 1 | 2 | 2 |
| Неравенства, сводящиеся к простейшим заменой неизвестного | 2 | 2 | |
| Введение вспомогательного угла | 1 | 2 | |
| Контрольная работа по теме «Тригонометрические уравнения и неравенства | 1 | 1 | 1 |
| Перпендикулярность прямых и плоскостей | 9 | 21 | 24 |
| Перпендикулярность прямой и плоскости | 1 | 2 | 3 |
| Решение задач | 1 | 3 | 4 |
| Перпендикуляр и наклонные | 2 | 3 | 4 |
| Угол между прямой и плоскостью | 1 | 3 | 3 |
| Двугранный угол | 1 | 3 | 3 |
| Перпендикулярность плоскостей | 1 | 5 | 5 |
| Итоговый урок по теме | 1 | 1 | 1 |
| Контрольная работа по теме «Перпендикулярность прямых и плоскостей» | 1 | 1 | 1 |
| Действительные числа | 8 | 18 | 21 |
| Понятие действительного числа | 1 | 1 | 2 |
| Множества чисел. Свойства действительных чисел | 1 | 2 | 2 |
| Метод математической индукции | 2 | 2 | |
| Перестановки | 1 | 2 | 2 |
| Размещения | 1 | 2 | 2 |
| Сочетания | 1 | 2 | 2 |
| Доказательство числовых неравенств | 1 | 2 | |
| Делимость целых чисел | 1 | 2 | 2 |
| Сравнение по модулю | 1 | 2 | |
| Задачи с целочисленными неизвестными | 1 | 2 | 2 |
| Контрольная работа по теме «Действительные числа» | 1 | 1 | 1 |
| Многогранники | 9 | 20 | 21 |
| Понятие многогранника. Призма | 2 | 5 | 5 |
| Пирамида | 2 | 5 | 5 |
| Правильные многогранники | 1 | 3 | 4 |
| Решение задач | 2 | 5 | 5 |
| Итоговый урок по теме | 1 | 1 | 1 |
| Контрольная работа по теме«Многогранники» | 1 | 1 | 1 |
| Рациональные уравнения и неравенства | 14 | 28 | 30 |
| Рациональные выражения | 2 | 2 | 3 |
| Формулы бинома Ньютона, суммы и разности степеней | 1 | 2 | 3 |
| Деление многочленов с остатком. Алгоритм Евклида | 2 | 2 | |
| Теорема Безу. Корень многочлена | 1 | 3 | 3 |
| Рациональные уравнения | 2 | 3 | 3 |
| Системы рациональных уравнений | 2 | 3 | 3 |
| Метод интервалов решения неравенств | 2 | 3 | 3 |
| Рациональные неравенства | 1 | 3 | 3 |
| Нестрогие неравенства | 1 | 3 | 3 |
| Системы рациональных неравенств | 1 | 3 | 3 |
| Контрольная работа по теме «Рациональные уравнения и неравенства» | 1 | 1 | 1 |
| Корень степени n | 8 | 14 | 18 |
| Понятие функции и ее графика | 1 | 1 | 2 |
| Функция у=х | 1 | 1 | 2 |
| Понятие корня степени n | 1 | 3 | 3 |
| Корни четной и нечетной степеней | 1 | 2 | 2 |
| Арифметический корень | 1 | 2 | 3 |
| Свойства корней степени n | 1 | 2 | 3 |
| Функция у=√х, х≥0 | 1 | 2 | 2 |
| Контрольная работа по теме «Корень степени n » | 1 | 1 | 1 |
| Степень положительного числа | 8 | 18 | 19 |
| Степень с рациональным показателем | 1 | 2 | 2 |
| Свойства степени с рациональным показателем | 1 | 2 | 3 |
| Понятие предела последовательности | 2 | 2 | |
| Свойства пределов | 2 | 2 | |
| Бесконечно убывающая геометрическая прогрессия | 1 | 2 | 2 |
| Число е | 1 | 2 | 2 |
| Понятие степени с иррациональным показателем | 2 | 3 | 3 |
| Показательная функция | 1 | 2 | 2 |
| Контрольная работа по теме «Степень положительного числа» | 1 | 1 | 1 |
| Логарифмы | 6 | 8 | 10 |
| Понятие логарифма | 2 | 2 | 3 |
| Свойства логарифмов | 2 | 3 | 4 |
| Логарифмическая функция | 2 | 3 | 3 |
| Показательные и логарифмические уравнения и неравенства | 6 | 14 | 14 |
| Простейшие показательные уравнения | 1 | 2 | 2 |
| Простейшие логарифмические уравнения | 1 | 2 | 2 |
| Уравнения, сводящиеся к простейшим заменой неизвестного | 1 | 3 | 3 |
| Простейшие показательные неравенства | 1 | 3 | 3 |
| Простейшие логарифмические неравенства | 1 | 2 | 2 |
| Неравенства, сводящиеся к простейшим заменой неизвестного | 1 | 2 | 2 |
| Повторение курса геометрии | 5 | 13 | 14 |
| Комбинаторика и вероятность | 9 | 19 | 21 |
| Правило умножения. Комбинаторные задачи. Перестановки и факториалы | 1 | 3 | 3 |
| Решение задач на применение описательных характеристик числовых наборов. Вычисление частот и вероятностей событий. Вычисление вероятностей в опытах с равновозможными элементарными исходами | 2 | 3 | 4 |
| Решение задач на применение описательных характеристик числовых наборов. Вычисление частот и вероятностей событий. Вычисление вероятностей в опытах с равновозможными элементарными исходами | 2 | 4 | 4 |
| Выбор нескольких элементов. Биноминальные коэффициенты. Решение уравнений степени выше 2 специальных видов. Теорема Виета, теорема Безу | 3 | 3 | |
| Случайные события и их вероятности. Вычисление вероятностей независимых событий | 2 | 3 | 3 |
| Использование формулы сложения вероятностей, диаграмм Эйлера, дерева вероятностей, формулы Бернулли | 1 | 2 | 3 |
| Контрольная работа по теме «Показательные и логарифмические уравнения и неравенства» | 1 | 1 | 1 |
| Повторение и систематизация учебного материала | 17 | 26 | 26 |
| Итоговая контрольная работа | 2 | 2 | 2 |
| Анализ контрольной работы | 1 | 1 | 1 |
11 класс 2019-2020 учебный год
| Содержание учебного материала | I - 11 А | II - 1 1 Б | III - 11 В |
| Функции и их графики | 13 | 29 | 29 |
| Элементарные функции | 1 | 3 | 3 |
| 02.09 | 02.09, 03.09 03.09 | 02.09, 03.09 03.09 | |
| Область определения и область изменения функции. Ограниченность функции | 1 | 1 | 1 |
| 03.09 | 04.09 | 03.09 | |
| Четность, нечетность, периодичность функций | 1 | 3 | 3 |
| 04.09 | 04.09, 04.09 05.09 | 04.09, 04.09 05.09 | |
| Промежутки возрастания, убывания, знакопостоянства и нули функции | 1 | 2 | 2 |
| 05.09 | 05.09, 06.09 | 06.09, 06.09 | |
| Исследование функций и построение их графиков элементарными методами | 2 | 3 | 3 |
| 09.09 10.09 | 09.09, 10.09 10.09 | 09.09, 10.09 10.09 | |
| Основные способы преобразования графиков | 2 | 2 | 2 |
| 11.09 12.09 | 11.09, 11.09 | 10.09, 11.09 | |
| Графики функций, содержащих модули | 1 | 2 | 2 |
| 16.09 | 11.09, 12.09 | 11.09, 12.09 | |
| Понятие предела функции | 1 | 1 | |
| 12.09 | 13.09 | ||
| Односторонние пределы | 1 | 1 | |
| 13.09 | 13.09 | ||
| Свойства пределов функций | 1 | 1 | |
| 16.09 | 16.09 | ||
| Понятие непрерывности функции | 1 | 1 | |
| 17.09 | 17.09 | ||
| Непрерывность элементарных функций | 1 | 1 | 1 |
| 17.09 | 17.09 | 17.09 | |
| Обратные функции Понятие обратной функции | 1 | 2 | 2 |
| 18.09 | 18.09 18.09 | 17.09, 18.09 18.09 | |
| Взаимно обратные функции | 1 | 2 | 2 |
| 19.09 | 18.09, 19.09 | 19.09 | |
| Обратные тригонометрические функции | 2 | 2 | |
| 19.09, 20.09 | 20.09, 20.09 | ||
| Примеры использования обратных тригонометрических функций | 1 | 1 | |
| 23.09 | 23.09 | ||
| Контрольная работа по теме «Функции» | 1 | 1 | 1 |
| 23.09 | 24.09 | 24.09 | |
| Векторы в пространстве | 5 | 9 | 9 |
| Понятие вектора | 1 | 2 | 2 |
| 24.09 | 24.09, 25.09 | 24.09, 24.09 | |
| Сложение и вычитание векторов. Умножение вектора на число | 2 | 3 | 3 |
| 25.09 26.09 | 25.09, 25.09, 26.09 | 25.09, 25.09, 26.09 | |
| Компланарные векторы | 1 | 3 | 3 |
| 30.09 | 26.09, 27.09, 30.09 | 27.09, 27.09 30.09 | |
| Итоговый урок по теме «Векторы в пространстве» | 1 | 1 | 1 |
| 01.10 | 01.10 | 01.10 | |
| Метод координат в пространстве | 10 | 24 | |
| Координаты точки и координаты вектора | 2 | 4 | 4 |
| 02.10, 03.10 | 01.10, 02.10, 02.10, 02.10 | 01.10, 01.10, 02.10, 02.10 | |
| Простейшие задачи в координатах | 2 | 4 | 4 |
| 07.10, 08.10 | 03.10, 03.10 04.10, 07.10 | 03.10, 04.10 04.10, 07.10 | |
| Угол между векторами. Скалярное произведение векторов | 1 | 4 | 4 |
| 09.09, 10.09 | 08.10, 08.10, 09.10, 09.09 | 08.10, 08.10, 08.10, 09.09 | |
| Решение задач | 2 | 6 | 6 |
| 14.10, 15.10 | 09.09, 10.10,10.10, 11.10, 14.10, 15.10 | 09.09, 10.10,11.10, 11.10, 14.10, 15.10 | |
| Движения | 1 | 4 | 4 |
| 16.10 | 15.10, 16.10, 16.10, 16.10 | 15.10, 15.10, 16.10, 16.10 | |
| Итоговый урок по теме: «Метод координат в пространстве» | 1 | 1 | 1 |
| 17.10 | 17.10 | 17.10 | |
| Контрольная работа по теме «Метод координат в пространстве» | 1 | 1 | 1 |
| 21.10 | 17.10 | 18.10 | |
| Производная | 15 | 40 | 40 |
| Понятие производной | 1 | 2 | 2 |
| 22.10 | 18.10, 21.10 | 18.10, 21.10 | |
| Производная суммы. Производная разности | 1 | 3 | 3 |
| 23.10 | 22.10, 22.10, 23.10 | 22.10, 22.10, 22.10 | |
| Непрерывность функций, имеющих производную. Дифференциал | 2 | 2 | |
| 23.10, 23.10 | 23.10, 23.10 | ||
| Производная произведения. Производная частного | 1 | 2 | 2 |
| 24.10 | 24.10, 24.10 | 24.10, 25.10 | |
| Производная элементарных функций | 1 | 3 | 3 |
| 05.11 | 25.10, 05.11, 05.11 | 25.10, 05.11, 05.11 | |
| Производная сложной функции | 3 | 3 | |
| 06.11, 06.11, 06.11 | 05.11, 06.11, 06.11 | ||
| Контрольная работа по теме «Производная» | 1 | 1 | 1 |
| 06.11 | 07.11 | 07.11 | |
| Максимум и минимум функции | 1 | 2 | 2 |
| 07.11 | 07.11, 08.11 | 08.11, 08.11 | |
| Уравнение касательной | 1 | 2 | 2 |
| 11.11 | 11.11, 12.11 | 11.11, 12.11 | |
| Приближенные вычисления. | 3 | 3 | |
| 12.11, 13.11 , 13.11 | 12.11, 12.11 , 13.11 | ||
| Возрастание и убывание функций | 1 | 3 | 3 |
| 12.11 | 13.11, 14.11, 14.11 | 13.11, 14.11 , 15.11 | |
| Производные высших порядков | 2 | 2 | |
| 15.11, 18.11 | 15.11, 18.11 | ||
| Экстремум функции с единственной критической точкой | 1 | 3 | 3 |
| 13.11 | 19.11, 19.11, 20.11 | 19.11, 19.11, 19.11 | |
| Задачи на максимум и минимум | 2 | 3 | 3 |
| 14.11, 18.11 | 20.11,20.11, 21.11 | 20.11,20.11, 21.11 | |
| Асимптоты. Дробно-линейные функции | 2 | 2 | |
| 21.11, 22.11 | 22.11, 22.11 | ||
| Построение графиков функций с применением производной | 3 | 3 | 3 |
| 19.11,20.11 21.11 | 25.11, 26.11, 26.11 | 25.11, 26.11, 26.11 | |
| Контрольная работа по теме «Применение производной» | 1 | 1 | 1 |
| 25.11 | 27.11 | 2 6 .11 | |
| Цилиндр, конус, шар | 10 | 24 | 24 |
| Цилиндр. Решение задач | 1 | 3 | 3 |
| 26.11 | 27.11, 27.11,28.11 | 27.11, 27.11,28.11 | |
| Конус. Площадь поверхности конуса | 1 | 3 | 3 |
| 27.11 | 28.11,29.11, 02.12 | 29.11,29.11, 02.12 | |
| Усеченный конус | 1 | 3 | 3 |
| 28.11 | 03.12,03.12, 04.12 | 03.12,03.12, 03.12 | |
| Сфера и шар. Уравнение сферы | 1 | 3 | 3 |
| 02.12 | 04.12,04.12,05.12 | 04.12,04.12, 05.12 | |
| Взаимное расположение сферы и плоскости | 3 | 3 | |
| 05.12,06.12, 09.12 | 06.12,06.12, 09.12 | ||
| Касательная плоскость к сфере. Площадь сферы | 1 | 3 | 3 |
| 03.12 | 10.12,10.12, 11.12 | 10.12,10.12, 10.12 | |
| Решение задач цилиндр, конус и шар | 3 | 4 | 4 |
| 04.12,05.12 09.12 | 11.12,11.12, 12.12,12.12 | 11.12,11.12, 12.12,13.12 | |
| Итоговый урок по теме: «Цилиндр, конус, шар» | 1 | 1 | 1 |
| 10.12 | 13.12 | 13.12 | |
| Контрольная работа по теме «Цилиндр, конус, шар» | 1 | 1 | 1 |
| 11.12 | 16.12 | 16.12 | |
| Первообразная и интеграл | 8 | 18 | 18 |
| Понятие первообразной | 1 | 2 | |
| 12.12 | 17.12, 17.12 | 17.12, 17.12 | |
| Площадь криволинейной трапеции | 1 | 2 | 2 |
| 16.12 | 18.12, 18.12 | 17.12, 18.12 | |
| Определенный интеграл | 1 | 2 | 2 |
| 17.12 | 18.12, 19.12 | 18.12, 19.12 | |
| Приближенное вычисление определенного интеграла | 3 | 3 | |
| 19.12,20.12, 23.12 | 20.12,20.12, 23.12 | ||
| Формула Ньютона-Лейбница | 2 | 3 | 3 |
| 18.12,19.12 | 24.12, 24.12, 25.12 | 24.12, 24.12, 24.12 | |
| Свойства определенных интегралов | 1 | 2 | 2 |
| 23.12 | 25.12, 25.12 | 25.12, 25.12 | |
| Применение определенных интегралов в геометрических и физических задачах | 1 | 3 | 3 |
| 24.12 | 26.12, 26.12, 13.01 (анализ к.р.) | 26.12, 27.12, 13.01 (анализ к.р.) | |
| Контрольная работа по теме «Первообразная и интеграл» | 1 | 1 | 1 |
| 25.12 | 27.12 | 27.12 | |
| Объемы тел | 10 | 24 | 24 |
| Объем прямоугольного параллелепипеда | 1 | 3 | 3 |
| 26.12 | 14.01,14.01, 15.01 | 14.01,14.01, 14.01 | |
| Объем прямой призмы и цилиндра | 1 | 3 | 3 |
| 13.01 | 15.01, 15.01,16.01 | 15.01, 15.01,16.01 | |
| Объем наклонной призмы | 1 | 4 | 4 |
| 14.01 | 16.01, 17.01,20.01 | 17.01, 17.01,20.01 | |
| Объем пирамиды и конуса | 1 | 4 | 4 |
| 15.01 | 21.01, 21.01, 22.01,22.01, | 21.01, 21.01, 21.01,22.01, | |
| Объем шара и площадь сферы | 1 | 4 | 4 |
| 16.01 | 22.01,23.01, 23.01,24.01 | 22.01,23.01, 24.01,24.01 | |
| Решение задач | 3 | 4 | 4 |
| 20.01,21.0122.01 | 27.01,28.01, 28.01,29.01 | 27.01,28.01, 28.01,28.01 | |
| Итоговый урок по теме «Объемы тел» | 1 | 1 | 1 |
| 23.01 | 29.01 | 29.01 | |
| Контрольная работа по теме «Объемы тел» | 1 | 1 | 1 |
| 2 7 .01 | 29 .01 | 29 .01 | |
| Уравнения и неравенства | 40 | 86 | 86 |
| Равносильные преобразования уравнений | 2 | 2 | 2 |
| 28.01,29.01 | 30.01,30.01 | 30.01,31.01 | |
| Равносильные преобразования неравенств | 2 | 2 | 2 |
| 30.01, 03.02 | 31.01, 03.02 | 31.01, 03.02 | |
| Понятие уравнения-следствия | 1 | 2 | 2 |
| 04.02 | 04.02,04.02 | 04.02,04.02 | |
| Возведение уравнения в четную степень | 1 | 2 | 2 |
| 05.02 | 05.02,05.02 | 04.02,05.02 | |
| Потенцирование логарифмических уравнений | 1 | 2 | 2 |
| 06.02 | 05.02,06.02 | 05.02,06.02 | |
| Другие преобразования, приводящие к уравнению-следствию | 1 | 2 | 2 |
| 10.02 | 06.02,07.02 | 07.02,07.02 | |
| Применение нескольких преобразований, приводящих к уравнению-следствию | 1 | 2 | 2 |
| 11.02 | 10.02,11.02 | 10.02,11.02 | |
| Равносильность уравнений и неравенств системам. Основные понятия | 1 | 2 | 2 |
| 12.02 | 11.02,12.02 | 11.02,11.02 | |
| Решение уравнений с помощью систем | 1 | 2 | 2 |
| 13.02 | 12.02, 12.02 | 12.02, 12.02 | |
| Решение уравнений с помощью систем (продолжение) | 1 | 2 | 2 |
| 17.02 | 13.02, 13.02 | 13.02, 14.02 | |
| Уравнения вида f(α(x))=f(β(x)) | 1 | 2 | 2 |
| 18.02 | 14.02, 17.02 | 14.02, 17.02 | |
| Решение неравенств с помощью систем | 1 | 2 | 2 |
| 19.02 | 18.02, 18.02 | 18.02, 18.02 | |
| Решение неравенств с помощью систем (продолжение) | 2 | 2 | |
| 19.02, 19.02 | 18.02, 19.02 | ||
| Неравенства вида f(α(x))>f(β(x)) | 2 | 2 | |
| 19.02,20.02 | 19.02,20.02 | ||
| Равносильность уравнений на множествах | |||
| Основные понятия | 1 | 2 | 2 |
| 20.02 | 20.02,21.02 | 21.02,21.02 | |
| Возведение уравнения в четную степень | 1 | 2 | 2 |
| 25.02 | 25.02,25.02 | 25.02,25.02 | |
| Умножение уравнения на функцию | 1 | 2 | 2 |
| 26.02 | 26.02,26.02 | 25.02,26.02 | |
| Другие преобразования уравнений | 1 | 2 | 2 |
| 27.02 | 26.02,27.02 | 26.02,27.02 | |
| Применение нескольких преобразований | 1 | 3 | 3 |
| 27.02,28.02 02.03 | 28.02,28.02 02.03 | ||
| Контрольная работа по теме «Равносильность уравнений» | 1 | 1 | 1 |
| 0 2.0 3 | 03.03 | 03.03 | |
| Равносильность неравенств на множествах Основные понятия | 1 | 2 | 2 |
| 03.03 | 03.03,04.03 | 03.03,03.03 | |
| Возведение неравенств в четную степень | 1 | 2 | 2 |
| 04.03 | 04.03,04.03 | 04.03,04.03 | |
| Умножение неравенств на функцию | 1 | 2 | 2 |
| 05.03 | 05.03,05.03 | 05.03,06.03 | |
| Другие преобразования неравенств | 1 | 2 | 2 |
| 10.03 | 06.03,10.03 | 06.03,10.03 | |
| Применение нескольких преобразований | 1 | 3 | 3 |
| 11.03 | 10.03,11.03 11.03 | 10.03,10.03 11.03 | |
| Нестрогие неравенства | 1 | 2 | 2 |
| 12.03 | 11.03, 12.03 | 11.03, 12.03 | |
| Уравнения с модулями | 1 | 3 | 3 |
| 16.03 | 12.03,13.03 16.03 | 13.03,13.03 16.03 | |
| Неравенства с модулями | 1 | 4 | 4 |
| 17.03 | 17.03, 17.03, 18.03, 18.03 | 17.03, 17.03, 17.03, 18.03 | |
| Метод интервалов для непрерывных функций | 1 | 3 | 3 |
| 18.03 | 18.03,19.03, 20 .03 (анализ к.р.) | 18.03,20.03, 20 .03 (анализ к.р.) | |
| Контрольная работа по теме «Равносильность неравенств» | 1 | 1 | 1 |
| 1 9 .03 | 19 .03 | 19 .03 | |
| Использование областей существования функции | 1 | 2 | 2 |
| 30.03 | 30.03,31.03 | 30.03,31.03 | |
| Использование неотрицательности функции | 1 | 2 | 2 |
| 31.03 | 31.03,01.04 | 31.03, 31.03 | |
| Использование ограниченности функции | 1 | 2 | 2 |
| 18.03 | 01.04,01.04 | 01.04,01.04 | |
| Использование монотонности и экстремумов функции | 1 | 2 | 2 |
| 01.04 | 02.04,02.04 | 02.04,03.04 | |
| Использование свойств синуса и косинуса | 1 | 2 | 2 |
| 02.04 | 03.04,06.04 | 03.04,06.04 | |
| Системы уравнений с несколькими неизвестными. Равносильность систем | 1 | 3 | 3 |
| 06.04 | 07.04,07.04 08.04 | 07.04,07.04 07.04 | |
| Система-следствие | 1 | 3 | 3 |
| 07.04 | 08.04,08.04 09.04 | 08.04,08.04 09.04 | |
| Метод замены неизвестных | 1 | 3 | 3 |
| 08.04 | 09.04,10.04 13.04 | 10.04,10.04 13.04 | |
| Рассуждения с числовыми значениями при решении уравнений и неравенств | 1 | 3 | 3 |
| 09.04 | 14.04,14.04 15.04 | 14.04,14.04 14.04 | |
| Контрольная работа по теме «Системы уравнений» | 1 | 1 | 1 |
| 13 .04 | 1 5 .04 | 1 5 .04 | |
| Комплексные числа | 2 | 12 | 12 |
| Алгебраическая форма комплексного числа | 1 | 3 | 3 |
| 14.04 | 15.04,16.04 16.04 | 15.04,16.04 17.04 | |
| Сопряженные комплексные числа | 3 | 3 | |
| 17.04,20.04 21.04 | 17.04,20.04 21.04 | ||
| Геометрическая интерпретация комплексного числа | 1 | 3 | 3 |
| 15.04 | 21.04,22.04 22.04 | 21.04,21.04 22.04 | |
| Тригонометрическая форма комплексного числа | 3 | 3 | |
| 22.04,23.04 23.04 | 22.04,23.04 24.04 | ||
| Повторение | 16 | 28 | 28 |
| Повторение. Параллельность прямых, прямой и плоскости. Скрещивающиеся прямые. Параллельность плоскостей | 1 | 2 | 2 |
| 16.04 | 24.04,27.04 | 24.04,27.04 | |
| Повторение. Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью | 2 | 4 | 4 |
| 20.04,21.04 | 28.04,28.04 29.04,29.04 | 28.04,28.04 28.04,29.04 | |
| Повторение. Двугранный угол. Перпендикулярность плоскостей | 2 | 4 | 4 |
| 22.04,23.04 | 29.04,30.04 30.04,04.05 | 29.04,30.04 04.05, 05.05 | |
| Повторение. Многогранники: параллелепипед, призма, пирамида, площади их поверхностей | 2 | 4 | 4 |
| 27.04, 28.04 | 05.05,05.05 06.05,06.05 | 05.05,05.05 06.05,06.05 | |
| Повторение. Цилиндр, конус и шар, площади их поверхностей | 2 | 3* | 3* |
| 29.04,30.04 | 06.05,07.05 07.05 | 07.05,08.05 08.05 | |
| Повторение. Объемы тел | 2 | 3* | 3* |
| 04.05,05.05 | 08.05,11.05 12.05 | 11.05,12.05 12.05 | |
| Уравнения. Неравенства | 3* | 4* | 4* |
| 06.05,07.05 11.05 | 12.05,13.05, 13.05,13.05 | 12.05,13.05, 13.05,14.05 | |
| Текстовые задачи | 3* | 4* | 4* |
| 12.05,13.05 14.05 | 14.05,14.05, 15.05,18.05 | 15.05,15.05, 18.05,19.05 | |
| Итоговая контрольная работа | 1 | 2 | 2 |
| 18.05 | 19.05,19.05 | 19.05,19.05 | |
| Анализ контрольной работы | 1 | 1 | 1 |
| 19.05 | 20.05 | 20.05 | |
| Резерв (повторение) | 20.05, 21.05, 25.05 | 20.05,20.05, 21.05,21.05, 22.05,25.05 | 20.05,21.05, 22.05,22.05, 25.05 |
Дата добавления: 2019-11-25; просмотров: 144; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!