Static void rank(ref int x, ref int y)
{
int m;
if (x > y)
{ m = x ; x = у ; у = m ; }
}
static void Main()
{
int i = 85, j = 23;
rank(ref i, ref j);
Console.WriteLine("i = {0}, j = {1}", i, j);
}
Обратите внимание на то, что модификатор ref используется не только перед параметром, но и перед замещающим его аргументом. Особо отметим, что аргументом может быть только переменная (не константа и не выражение) того же типа, что и параметр.
Параметр с модификатором ref должен быть инициализирован в вызывающем модуле.
Выходные параметры снабжаются модификатором out и позволяют присвоить значения объектам вызывающего метода даже в тех случаях, когда эти объекты значений еще не имели.
В качестве иллюстрации применения выходных параметров приведем метод, возвращающий целую ( int integer) и дробную ( double tra) части вещественного числа ( double x). В функции Main() определим три переменных: double real — исходное число, double dPart - дробная часть, int iPart — целая часть. Переменная real инициализирована, переменные iPart, dPart не имеют значений до обращения к методу.
Static void fun(double х , out int integer, out double fra)
{ integer = (int)x; fra= x — integer; }
Static void Main()
{ double real = 53.93;
double dPart;
int iPart;
fun(real, out iPart, out dPart);
Console.WriteLine("iPart = {0}, dPart = {1}",iPart, dPart); }
В блок-схеме программы блок-схема процедуры, как и блок-схема функции, изображается отдельно. В блок-схеме основной программы оператор вызова подпрограммы изображается в виде блока:
Примеры
Пример 6.
Дана дробь в виде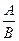 
(А, В – натуральные числа). Представить эту дробь в виде несократимой дроби.
|
|
|
Исходные данные: A – числитель, целый тип и B – знаменатель, целый тип.
Результат: A – числитель после сокращения, В – знаменатель после сокращения.
Для сокращения дроби надо найти наибольший общий делитель (НОД) для числителя и знаменателя, а затем разделить числитель и знаменатель на это число.
Сокращение дроби запишем в отдельной viod-функции SOKR. Эта viod-функция в дальнейшем может быть использована в других задачах.
Данную задачу можно решить только с использованием viod-функции, т.к. в результате этой подпрограммы изменяются входные параметры.
Обратите внимание, что функция NOD, которая была рассмотрена в предыдущей лабораторной работе, в данном примере представлена как viod-функция.
Любая функция может быть представлена как void-функция. В этом случае, полученный результат является еще одним параметром void-функции, причем параметром, передаваемым по ссылке.
В данном примере используется две void-функции: void-функция NOD, для нахождения наибольшего общего делителя и void-функция SOKR для сокращения числителя и знаменателя. Void-функция SOKR вызывает процедуру NOD, поэтому в описании прототипов void-функция NOD должна предшествовать void-функции SOKR
|
|
|
Тестовый пример:
При А=7, В=56, после сокращения получаем А=1, В=8.
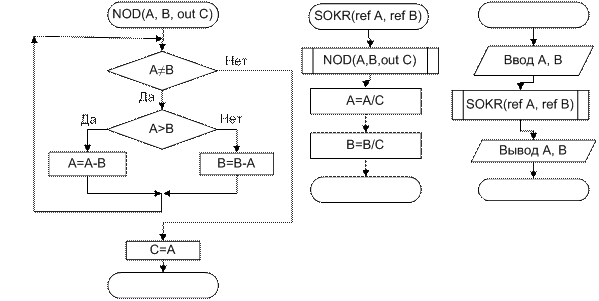
//Нахождение наибольшего общего делителя - C
public static void NOD(int A, int B, out int C)
{while (A!=B)
{if (A>B)
A=A-B;
else B=B-A;
}
C=A;
}
// сокращение дроби A/B
public static void SOKR(ref int A, ref int B);
{int C;
NOD(A, B, out C);
A=A/C;
B=B/C;
}
static public void Main(string[] args)
{int a,b;
Console.Write("a=");
a=Convert.ToInt32(Console.ReadLine());
Console.Write("b=");
b=Convert.ToInt32(Console.ReadLine());
SOKR(ref a, ref b);
Console.WriteLine("a= {0} b={1}", a,b);
C0nsoleReadKey();
}
Пример 7.
Дана последовательность из n натуральных чисел. Для каждого числа указать его наименьший и наибольший делитель. Для простого числа – 1 и само число, для остальных это должны быть числа отличные от 1 и самого числа.
Исходные данные: n- количество элементов последовательности. а – элемент последовательности.
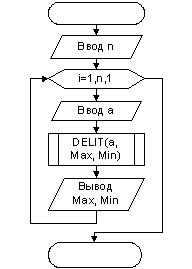Результат: Max – наибольший делитель, Min – наименьший делитель каждого элемента последовательности.
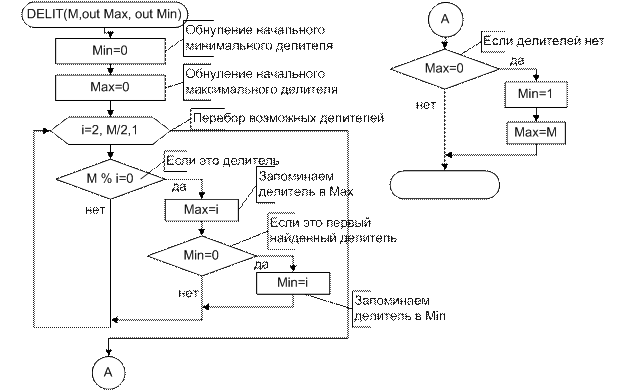
Нахождение наибольшего и наименьшего делителя выполняется в процедуре DELIT. Void-функция в этом случае используется потому, что в результате получается не одно значение, а два.
Тестовый пример:
при n=5 и
a=6, Max=3, Min-2
a=7, Max=7, Min=1
a=24, Max=12, Min=2
a=15, Max=5, Min=3
a=63, Max=7, Min=3
Пример 8.
Найти все натуральные числа, не превосходящие заданное N, которые делятся на каждую из своих цифр.
|
|
|
Исходные данные: N – целый тип.
Результат: Вывод чисел, которые делятся на каждую из своих цифр.
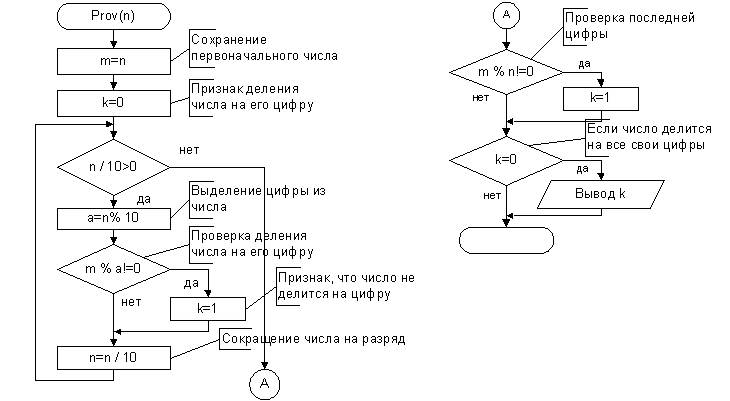
В процедуре Prov проверяется делится ли число на все свои цифры, если делится - данное число выводится на экран. Результатом процедуры является печать чисел, удовлетворяющих заданному условию.
Тестовый пример:
При N=20 выводятся числа: 1,2,3,4,5,6,7,8,9,10,11,12,15,20
Приведен пример блок-схемы процедуры Prov, которая проверяет деление числа на свои цифры.
Задание 2 Написать и отладить программу для примера 7.
Контрольные вопросы
1. Можно ли в Примере 6 при вычислении NOD параметры A и B описать как параметры, передаваемые по ссылке.
2. Можно ли в Примере 6 поменять местами описание void-функции NOD и SOKR.
3. Перечислите преимущества void-функций перед функциями.
4. Чем параметры передаваемые по ссылке отличаются от параметров передаваемых по значению.
5. Можно ли в Примере 6 использовать не viod-функцию, а функцию.
6. В каких случаях viod-функцию можно заменить на функцию.
7. Можно ли в качестве фактических параметров по ссылке использовать выражения.
8. В каких ситуациях удобнее использовать функцию вместо viod-функции.
Индивидуальные задания
|
|
|
Создать методы-процедуры в отдельном классе.
1. Даны две дроби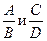 
(A, B, C, D – натуральные числа). Составить программу вычитания этих дробей. Результат должен быть несократимой дробью.
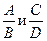
2. Даны две дроби (A, B, C, D – натуральные числа). Составить программу для деления этих дробей. Результат должен быть несократимой дробью.
3. Даны натуральные n, m и последовательности вещественных чисел х1, х2, …, хn, y1, y2, …, ym. Найти разности максимумов и минимумов каждой последовательности.
4. Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например, 41 и 43). Напечатать все пары «близнецов» из отрезка [n, 2n], где n – заданное натуральное число.
5. Дано натуральное n-значное число. Оставить в этом числе только первую цифру, а остальные заменить нулями.
6. Дано натуральное число N. Вывести все совершенные числа, которые <=N. Совершенным называется число равное, сумме своих делителей.
7. Дана последовательность из n натуральных чисел и натуральное число А. Найти в данной последовательности число, которое имеет самый большой наибольший общий делитель с числом А.
8. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N-1, у которых сумма всех цифр совпадает с суммой цифр данного числа.
9. Найти все натуральные n-значные числа, цифры в которых образуют строго возрастающую последовательность (например, 1234).
10. Из заданного числа вычли сумму его цифр. Из результата вновь вычли сумму его цифр и т.д. сколько таких действий надо произвести, чтобы получить нуль?
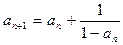
11. Для последовательности а1=1, 
составить программу печати k-того члена в виде обыкновенной несократимой дроби.
12. Дано четное число n>2. Проверить для него гипотезу Гольдбаха: каждое четное n представляется в виде суммы двух простых чисел.
Рекурсия*
Теория
Рекурсия – это такой способ организации вычислительного процесса, при котором процедура или функция в ходе выполнения составляющих ее операторов обращается сама к себе.
В рекурсивной процедуре или функции обязательно должно содержаться условие окончания рекурсии.
При выполнении рекурсии, когда подпрограмма доходит до рекурсивного вызова, процесс приостанавливается и новый процесс запускается с начала , но уже на новом уровне. Прерванный же процесс запоминается. Новый процесс тоже может быть приостановлен и т.д. Образуется последовательность прерванных процессов. Последовательность рекурсивных обращений должна обязательно выходить на определенное значение.
При каждом очередном входе в подпрограмму ее локальные параметры и адреса возврата размещаются в специальной области памяти – стеке. После выхода на определенной значение выполняется обратный ход- цепочка вычислений по обратному маршруту, сохраненному с стеке.
Пример 9.
Рассмотрим это на примере функции вычисления факториала. Хорошо известно, что 0!=1, 1!=1. А как вычислить величину n! для большого n? Если бы мы могли вычислить величину (n-1)!, то тогда мы легко вычислим n!, поскольку n!=n*(n-1)!. Но как вычислить (n-1)!? Если бы мы вычислили (n-2)!, то мы сможем вычислить и (n-1)!=(n-1)*(n-2)!. А как вычислить (n-2)!? Если бы... В конце концов, мы дойдем до величины 0!, которая равна 1. Таким образом, для вычисления факториала мы можем использовать значение факториала для меньшего числа. Блок-схема этого алгоритма выглядит следующим образом:
Программа соответствующего алгоритма имеет вид:
int factorial (int n)
{
if (n == 0)
{
return 1;
}
else
{
return n * factorial(n - 1);
}
}
Программа вызова рекурсивной функции вычисления факториала будет иметь вид:
Рекурсивные функции являются мощным механизмом в программировании. К сожалению, они не всегда эффективны. Также часто использование рекурсии приводит к ошибкам, наиболее распространенная из таких ошибок – бесконечная рекурсия, когда цепочка вызовов функций никогда не завершается и продолжается, пока не кончится свободная память в компьютере. Две наиболее распространенные причины для бесконечной рекурсии:
1. Неправильное оформление выхода из рекурсии. Например, если мы в программе вычисления факториала забудем поставить проверку if (n == 0), то factorial(0) вызовет factorial(-1), тот вызовет factorial(-2) и т.д.
2. Рекурсивный вызов с неправильными параметрами. Например, если функция factorial(n) будет вызывать factorial(n), то также получится бесконечная цепочка.
Поэтому при разработке рекурсивной функции необходимо прежде всего оформлять условия завершения рекурсии и думать, почему рекурсия когда-либо завершит работу.
Общее требование к задачам с рекурсией: когда вы сдаёте задачу, использующую рекурсию, вы устно обосновываете, почему рекурсия всегда когда-нибудь закончится.
Еще один пример рекурсивной void-функции:
viod Rec(int a)
{ if (a>0) Rec(a-1);
cout<<a<<endl;
}
Рассмотрим, что произойдет, если в основной программе поставить вызов, например, вида Rec(3). Ниже представлена блок-схема, показывающая последовательность выполнения операторов.
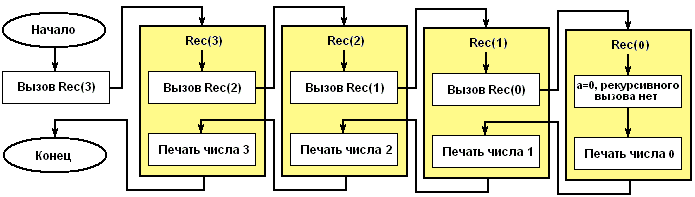
Void-функция Rec вызывается с параметром a = 3. В ней содержится вызов void-функции Rec с параметром a = 2. Предыдущий вызов еще не завершился, поэтому можете представить себе, что создается еще одна void-функция и до окончания ее работы первая свою работу не заканчивает. Процесс вызова заканчивается, когда параметр a = 0. В этот момент одновременно выполняются 4 экземпляра void-функции. Количество одновременно выполняемых void-функций называют глубиной рекурсии.
Четвертая вызванная void-функция (Rec(0)) напечатает число 0 и закончит свою работу. После этого управление возвращается к void-функции, которая ее вызвала (Rec(1)) и печатается число 1. И так далее пока не завершатся все void-функции. Результатом исходного вызова будет печать четырех чисел: 0, 1, 2, 3.
Еще один визуальный образ происходящего представлен на рисунке.
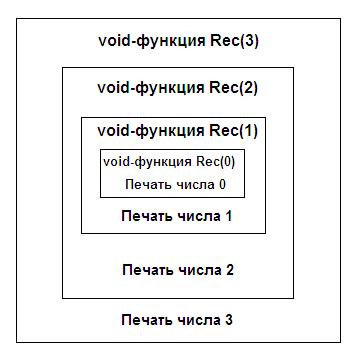
Выполнение void-функции Rec с параметром 3 состоит из выполнения void-функции Rec с параметром 2 и печати числа 3. В свою очередь выполнение void-функции Rec с параметром 2 состоит из выполнения void-функции Rec с параметром 1 и печати числа 2. И т. д.
Использование рекурсивных подпрограмм – красивый прием с точки зрения программирования. Программа выглядит более компактно. Но у рекурсии есть недостатки: рекурсия выполняется более медленно и глубина рекурсии ограничена.
Примеры
Пример 1.
Даны действительные числа x и ε (x≠0, ε > 0). Вычислить сумму с точностью ε.
Исходные данные: x – вещественный тип, точность eps – вещественный тип.
Результат: сумма summa – вещественный тип.
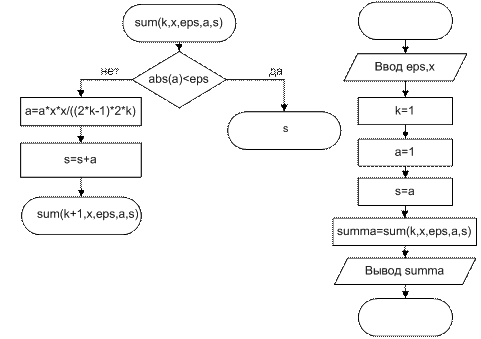
Вычисление суммы выполняем в функции sum. Рекуррентная формула, которая используется при вычислении суммы: ak=ak-1×(x2)/((2k-1)(2k)). Вызов функции заканчивается при abs(a)<eps. Начальное значение a0=1. Это значение суммируется в основной программе.
Тестовый пример: при x=4, eps=0.0001, summa=27.3082
namespace Сумма
{
class Program
{
static double summ(int k, double x, double eps, ref double a, ref double s)
{
if (Math.Abs(a) < eps) return s;
else
{
a = a * x * x / ((2 * k - 1) * 2 * k);
s = s + a;
return summ(k + 1, x, eps, ref a, ref s);
}
}
static void Main(string[] args)
{
double summa;
double eps = 0.0001f;
double x = 4f;
int k = 1;
double a = 1f;
double s = a;
summa = summ(k,x,eps, ref a, ref s);
Console.WriteLine("summa={0}", summa);
Console.ReadKey();
}
}
}
Пример 2.
Подсчитать количество цифр в заданном натуральном числе.
Исходные данные: заданное число N – целый тип.
Результат: количество цифр k – целый тип.
В рекурсивной функции заданное число делится на 10, для уменьшения количества цифр. Деление прекращается, когда результатом деления будет ноль. Это граничное условие для рекурсии.
Тестовый пример:
при N=5674, k=4.
Приведем пример с рекурсивной процедурой.
Пример 3.
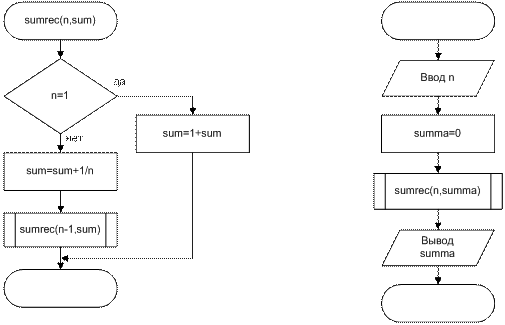
Вычислить сумму n членов ряда: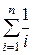 
Исходные данные: количество слагаемых n – целый тип.
Результат: сумма ряда summa – целый тип.
Тестовый пример:
при n=5 summa=2.2833
namespace Рекурсия
{
class Program
{ static void sumrec(int n, ref double sum)
{if (n==1) sum=1+sum;
else {sum=sum+1.0/n;
sumrec(n-1,ref sum);
}
}
static void Main(string[] args)
{
int n;
double summa = 0;
Console.WriteLine("n");
n = Convert.ToInt32(Console.ReadLine());
sumrec(n, ref summa);
Console.WriteLine("summa={0}", summa);
Console.ReadKey();
}
}
}
Задание Написать и отладить программу для примера 2.
Контрольные вопросы
1. Какая подпрограмма называется рекурсивной.
2. Почему в рекурсивной подпрограмме отсутствуют операторы цикла.
3. Может ли в рекурсивной подпрограмме отсутствовать развилка.
4. Почему в Примере 10 отсутствует операция k=k+1.
5. Как будет работать рекурсивная подпрограмма в Примере 10 при eps=0.1 и x=1.
6. Как будет работать рекурсивная подпрограмма в Примере 11 при k=333.
7. В Примере 12 укажите параметры по ссылке и параметры по значению в процедуре sumrec.
Дата добавления: 2019-11-16; просмотров: 360; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!