Пределы применимости формулы Эйлера

Формула Эйлера выполняется только в пределах упругих де­формаций.

Таким образом, критическое напряжение должно быть меньше предела упругости материала.

Предел упругости при расчетах можно заменять пределом про­порциональности. Таким образом, σ_кр ≤ σ_у ≈ σ _пц , где σ_у — предел упругости; σ_ПЦ — предел пропорциональности материала;

       

Предельная гибкость зависит от материала стержня.

В случае, если λ < λ_пред в материале стержня возникают оста­точные деформации. Поскольку в реальных конструкциях могут воз­никать пластические деформации, не приводящие к потере работо­способности, созданы эмпирические формулы для расчетов в этих случаях.

Расчет критического напряжения по формуле Ф. О. Ясинского  

Для стальных стержней

 

294                                                                                         Лекция 36

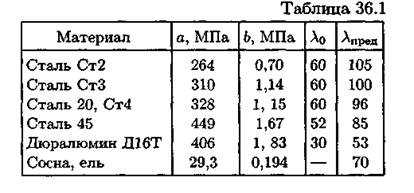
Критическое напряжение определяется по формуле σ_кр = а - bλ , где а и b — коэффициенты, зависящие от материала; их значения представлены в таблице.

На рис. 36.4 представлена зависимость критического напряже­ния от гибкости стержня.

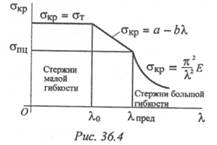Для стержней малой гибко­сти проводится расчет на сжа­тие σсж ≤ [σ]сж. Для стерж­ней средней гибкости расчет проводят по формуле Ясинского σ_кр = а - bλ .

    Для   стержней   большой   гиб­кости  расчет  проводят  по  фор­муле  Эйлера    σ_кр = π²Е/λ².

     Критическую силу при рас­чете критического напряжения по формуле Ясинского можно определить как

Fк_Р = σ_крА = (a - bλ)А .

      Условие устойчивости: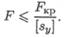

Контрольные вопросы и задания

1. Какое равновесие называется устойчивым?

2. Какие брусья следует рассчитывать на устойчивость?

3. Какую силу при расчете на устойчивость называют критиче­ской?

4. Напишите формулу Эйлера для расчета критической силы и назовите входящие величины и их единицы измерения.

5. Что называют гибкостью стержня, какой смысл заложен в этом названии? Назовите категории стержней в зависимости от гиб­кости.

6. От каких параметров стержня зависит предельная гибкость?

7. При каких условиях можно использовать формулу Эйлера для расчета критической силы?

8. В чем заключается расчет сжатого стержня на устойчивость? Напишите условие устойчивости. Чем отличается допускаемая сжи­мающая сила от критической?

               Тема 2.10. Устойчивость сжатых стержней                                   295

ЛЕКЦИЯ 37

           

Тема 2.10. Устойчивость сжатых стержней.

Расчеты на устойчивость

Знать условие устойчивости сжатых стержней, формулы Эйлера для определения критической силы, эмпирические формулы для расчетов критического напряжения и критической силы.

Уметь выполнять проверочные расчеты на устойчивость сжатых стержней.

          

Порядок выполнения расчета на устойчивость

1.Получение сведений о материале стержня для определения
предельной гибкости стержня расчетным путем или по таблице:

           

2. Получение сведений о геометрических размерах поперечного сечения, длине и способах закрепления концов для определения категории стержня в зависимости от гибкости:

            

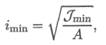
где А — площадь сечения; J_min— минимальный момент инерции (из осевых);

              

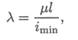
μ — коэффициент приведенной длины.

3. Выбор расчетных формул для определения критической силы
и критического напряжения.

При λ0 < λ < λ _пред — расчет по эмпирическим формулам.

При λ > λ _пред — расчет по формуле Эйлера.

4. Проверка и обеспечение устойчивости.

296                                                                                                                 Лекция 37

При расчете по формуле Эйлера условие устойчивости:

             

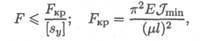
F — действующая сжимающая сила; [ s_y ] — допускаемый коэффици­ент запаса устойчивости.

При расчете по формуле Ясинского σ_кр = а - bλ , где а, b — расчетные коэффициенты, зависящие от материала (величины ко­эффициентов приводятся в таблице 36.1)

                

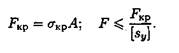
В случае невыполнения условий устойчивости необходимо уве­личить площадь поперечного сечения.

Иногда необходимо определить запас устойчивости при задан­ном нагружении: 

                                                   

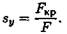
При проверке устойчивости сравнивают расчетный запас выно­сливости с допускаемым: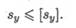                                      

Примеры решения задач

Пример 1. Рассчитать гибкость стержня. Круглый стержень диаметром 20 мм закреплен так, как показано на рис. 37.1.

Решение

                                               

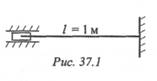
        1. Гибкость стержня определяется по формуле

λ  = μ l / i_{min .}

           2. Определяем минимальный радиус  инерции для круга.

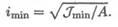
                Тема 2.10. Устойчивость сжатых стержней                                  297

 

Подставив выражения для Jmin и А (сечение — круг)

              

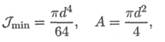
получим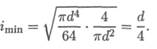                                    

3. Коэффициент приведения длины для данной схемы крепления μ = 0,5.

4. Гибкость стержня будет равна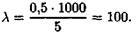  

Пример 2. Как изменится критическая сила для стержня, ес­ли изменить способ закрепления концов? Сравнить представленные схемы (рис. 37.2)

                

       

Решение

        

 

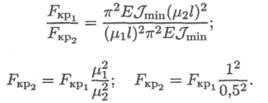
Критическая сила увеличится в 4 раза. F_KP2 = 4F_KPl.

Пример 3. Как изменится критическая сила при расчете на устойчивость, если стержень двутаврового сечения (рис. 37.3а, дву­тавр № 12) заменить стержнем прямоугольного сечения той же пло­щади (рис. 37.3b)? Остальные параметры конструкции не меняются. Расчет выполнить по формуле Эйлера.

298                                                                     Лекция 37

Решение

   

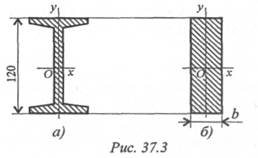
1. Определим ширину сечения прямоугольника, высота сечения
равна высоте сечения двутавра. Геометрические параметры двутавра № 12 по ГОСТ 8239-89 следующие:

площадь сечения А1= 14,7 см²;

  минимальный из осевых моментов инерции J_y = 27,9 см⁴.

  По условию площадь прямоугольного сечения равна площади сечения двутавра. Определяем ширину полосы при высоте 12 см.

                 

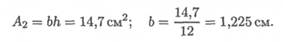
2. Определим минимальный из осевых моментов инерции.

                   

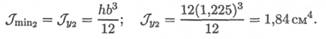
3. Критическая сила определяется по формуле Эйлера:

            

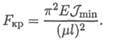
4. При прочих равных условиях отношение критических сил равно отношению минимальных моментов инерции:

             

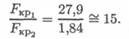
5. Таким образом, устойчивость стержня с сечением двутавр
№ 12 в 15 раз выше, чем устойчивость стержня выбранного прямоугольного сечения.

          Тема 2.10. Устойчивость сжатых стержней                                299

Пример 4. Проверить устойчивость стержня. Стержень дли­ной 1м защемлен одним концом, сечение — швеллер № 16, мате­риал — СтЗ, запас устойчивости трехкратный. Стержень нагружен сжимающей силой 82 кН (рис. 37.4).

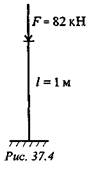                        Решение

1. Определяем основные геометрические пара­ метры сечения  стержня по ГОСТ 8240-89.

Швеллер № 16: площадь сечения 18,1см²; ми­нимальный осевой момент сечения 63,3 см⁴; мини­мальный радиус инерции сечения i_min = 1,87 см.

2. Определяем категорию стержня в зависимости от гибкости.

Предельная гибкость для материала СтЗ λпред = 100.

Расчетная гибкость стержня при длине l = 1м = 1000мм

                                       

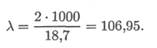
Рассчитываемый стержень — стержень большой гибкости, рас­чет ведем по формуле Эйлера.

              

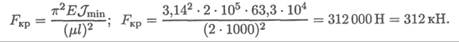
3. Допускаемая нагрузка на стержень [ F ] = F_Kp / [ s_y ].

               

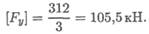
4. Условие устойчивости F ≤ [ F_y ];

82 кН < 105,5 кН.  Устойчивость стержня обеспечена.

300                                                               Лекция 37

---

Дата добавления: 2019-09-13; просмотров: 2439; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!