Классификация по характеристикам управления
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Старооскольский технологический институт
им. А.А. УГАРОВА
(филиал) федерального государственного автономного образовательного учреждения высшего профессионального образования
«Национальный исследовательский технологический университет «МИСиС»
Кафедра АИСУ
Халапян С.Ю.
ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ
Учебное пособие (курс лекций)
для студентов направления
230400 – «Информационные системы и технологии»
(для всех форм обучения)
Одобрено редакционно-издательским советом института
Старый Оскол
2014
УДК 681.5.01
ББК 32.965
Рецензент: к.т.н., директор ЗАО «Проектэлектромонтаж»
Ю.М. Пожарский.
Халапян С.Ю. Основы теории управления. Учебное пособие (курс лекций). Старый Оскол: СТИ НИТУ «МИСиС», 2014. – 90 с.
Учебное пособие (курс лекций) по курсу
«Основы теории управления» для студентов направления
230400 – «Информационные системы и технологии»,
для всех форм обучения.
© Халапян С.Ю.
© СТИ НИТУ «МИСиС»
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ. 4
Цель и задачи дисциплины.. 5
Требования к уровню освоения содержания дисциплины.. 5
1. Теория автоматического управления. Основные определения. 6
2. Классификация САУ.. 7
2.1 Классификация по характеру динамических процессов в системе. 7
2.2 Классификация по характеристикам управления. 9
|
|
|
2.3 Классификация САУ по другим признакам. 13
3. Функциональная и структурная схемы САУ.. 14
4. Статическая характеристика САУ.. 15
5. Уравнение движения и передаточная функция. 17
6. Типовые воздействия и временные характеристики САУ.. 20
7. Частотные характеристики САУ.. 23
8. Позиционные звенья САУ.. 27
8.1 Безынерционное звено. 27
8.2 Апериодическое (инерционное) звено I-го порядка. 29
8.3 Позиционные звенья II порядка. 31
9. Непозиционные звенья САУ.. 37
9.1 Интегрирующие звенья. 37
9.2 Дифференцирующие звенья. 39
10. Типовые соединения звеньев в структурных схемах САУ.. 41
11. Правила эквивалентного преобразования структурных схем. 43
12. Передаточные функции замкнутой системы.. 44
13. Устойчивость САУ. Правило Ляпунова. 45
14. Алгебраический критерий Гурвица. 48
15. Критерий устойчивости Рауса. 50
16. Критерий устойчивости Михайлова. 51
17. Критерий Найквиста. 54
18. Запас устойчивости. 58
19. Качество переходного процесса. 60
19.1 Оценка качества по переходной характеристике. 60
19.2 Оценка качества по частотной характеристике. 64
19.3 Корневые критерии качества переходного процесса. 70
19.4 Интегральные критерии качества переходного процесса. 72
20. Точность САУ.. 76
|
|
|
20.1 Коэффициенты ошибок. 76
20.2 Методы повышения точности. 77
21. Регуляторы. Законы регулирования. 81
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.. 88
ПРЕДИСЛОВИЕ
Теория управления (ТУ) – научная дисциплина, предметом изучения которой являются информационные процессы, протекающие в автоматических системах управления. ТУ выявляет общие закономерности функционирования, присущие автоматическим системам различной физической природы, и на основе этих закономерностей разрабатывает принципы построения высококачественных систем управления.
При изучении процессов управления в ТУ абстрагируются от физических и конструктивных особенностей систем и вместо реальных систем рассматривают их адекватные математические модели, поэтому основным методом исследования в ТУ является математическое моделирование. Кроме того, методическую основу ТУ образуют теория обыкновенных дифференциальных уравнений, операционное исчисление (преобразование Лапласа), гармонический анализ (преобразование Фурье).
ТУ вместе с теорией функционирования элементов систем управления (датчиков, регуляторов, исполнительных механизмов) образует более широкую отрасль науки – автоматику. Автоматика в свою очередь является одним из разделов технической кибернетики. Техническая кибернетика изучает сложные автоматизированные системы управления технологическими процессами (АСУТП) и предприятиями (АСУП), построенные с использованием управляющих вычислительных машин (УВМ). В настоящее время ТУ играет важную роль в совершенствовании и автоматизации управления производством.
|
|
|
Автоматизация является одним из главных направлений научно-технического прогресса и важным средством повышения эффективности производства. Современное промышленное производство характеризуется ростом масштабов и усложнением технологических процессов, применением интенсивных высокоскоростных режимов, близких к критериям, повышением требований к качеству продукции, безопасности персонала, экономичное, надежное и безопасное функционирование сложных объектов может быть обеспечено с помощью лишь самых совершенных принципов и технических средств управления.
Цель и задачи дисциплины
Цель преподавания дисциплины –
формирование системы теоретических знаний о системах автоматического управления, методах их анализа и синтеза.
Задачи изучения дисциплины –
освоить в результате изучения дисциплиныметоды:
|
|
|
· анализа устойчивости систем автоматического управления технологическими процессами;
· анализа качества переходных процессов и точности САУ;
· синтеза алгоритмов функционирования автоматических устройств;
· определения оптимальных условий протекания процессов и выбора необходимых структурных схем систем управления
и получить практические навыки решения соответствующих инженерных задач.
Требования к уровню освоения содержания дисциплины
В результате изучения дисциплины студенты должны
знать:
1) классификацию систем управления по различным основаниям;
2) временные и частотные характеристики типовых звеньев;
3) типовые соединения звеньев и их передаточные функции;
4) методы теории устойчивости систем управления;
5) прямые и косвенные методы оценки качества переходных процессов;
6) методы оценки точности САУ и ее повышения;
7) законы регулирования и их применение в управляющих устройствах.
уметь:
1) выполнять эквивалентное преобразование структурных схем и расчет передаточных функций сложных соединений звеньев;
2) определять устойчивость системы управления с помощью различных критериев устойчивости.
1. Теория автоматического управления.
Основные определения
Автоматика – отрасль науки и техники, занимающаяся вопросами создания, эксплуатации и последующей модернизации автоматических и автоматизированных систем.
Система автоматического управления (САУ) – это система, в которой автоматизированы все функции управления, и участие человека в работе системы не требуется.
Автоматизированная система управления (АСУ) - это система, в которой часть управляющих функций выполняется автоматическими управляющими устройствами, а часть функций (наиболее важных и сложных) выполняется человеком.
Теория автоматического управления – научная дисциплина, изучающая теоретические основы анализа и синтеза систем автоматического управления.
Упрощенная схема САУ:
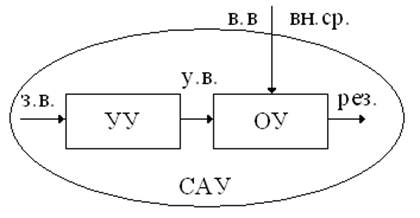
Объект управления (ОУ) – это устройство (совокупность устройств), установка или процесс осуществляющее технический процесс и нуждающееся в специально организованных воздействиях извне для осуществления его алгоритма функционирования.
Алгоритм функционирования устройства (системы) – это совокупность предписаний, ведущих к правильному выполнению технического процесса в устройстве (системе).
Алгоритм управления – это совокупность предписаний, определяющая характер воздействий извне на объект с целью осуществления его алгоритма функционирования.
Автоматическое управление - это процесс осуществления воздействий, соответствующих алгоритму управления.
Автоматическое управляющее устройство (УУ) – это устройство, специально созданное в система управления с целью формирования управляющего воздействия (у.в.) в соответствии с алгоритмом управления.
Алгоритм функционирования УУ – это и есть алгоритм управления.
Задающее воздействие (з.в.) – это поступающее в систему из внешней среды информация о целях и задачах управления.
Возмущающее воздействие (в.в.) – это вредное воздействие внешней среды (вн.ср.) на объект управления, обычно мешающее достижению цели в управлении.
Результат управления (рез.) – это определенное состояние объекта управления, значение некоторой физической величины, позволяющее судить о степени достижения цели управления, алгоритма функционирования ОУ.
Таким образом, система автоматического управления - это совокупность управляемого объекта и автоматического управляющего устройства (регулятора), взаимодействующих между собой.
2. Классификация САУ
2.1 Классификация по характеру динамических процессов в системе
По виду сигналов, протекающих по контуру системы, САУ бывают:
непрерывные - это такие системы, в которых во всех звеньях непрерывному во времени входному сигналу соответствует непрерывный во времени выходной сигнал. Для того чтобы система была непрерывная, необходимо наличие непрерывных статических характеристик системы.
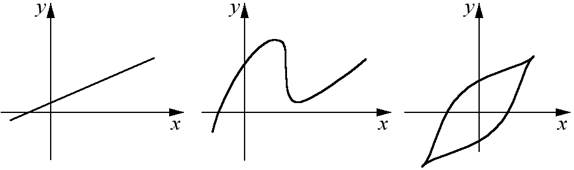
дискретные САУ- это такие системы, в которых хотя бы в одном звене непрерывному входному сигналу соответствует дискретный выходной сигнал (или импульс). К дискретным системам, как разновидность, относятся цифровые САУ, в которых функции регулятора выполняет цифровое устройство, а выходная величина представляет собой цифры.
релейные САУ (системы релейного действия) - это системы, в которых хотя бы в одном звене непрерывной входной величине соответствует выходная величина, изменяющаяся скачком. Статическая характеристика релейных систем имеет точку разрыва.
По виду дифференциальных уравнений:
Линейные
А) Обыкновенные линейные системы (с сосредоточенными параметрами) – это такие системы, в которых в каждом из звеньев динамические процессы описываются обыкновенными линейными уравнениями. Статическая характеристика таких систем имеет линейный вид.
Б) Особые линейные системы, среди которых различают:
линейные САУ с распределенными (в пространстве) параметрами - это такие САУ, динамика которых описывается частными производными, например, сушильные барабаны, флотомашины и другие установки, в которых процессы преобразования энергии и вещества происходят по всей длине аппарата.
линейные системы с запаздыванием - это такие САУ, в которых присутствует хотя бы одно звено чистого запаздывания (непрерывному входному сигналу соответствует непрерывный выходной сигнал, сдвинутый по времени на t, где t - время запаздывания).
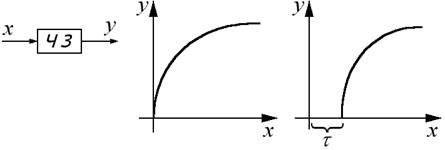
Нелинейные системы - это такие САУ, в которых хотя бы одно звено описывается нелинейным уравнением или имеется нелинейность иного вида, такая как произведение двух переменных, квадратный корень, степень и др.
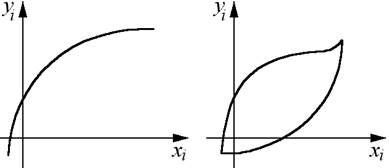
Среди нелинейных систем также выделяют особые нелинейные системы:
1. нелинейные системы с распределенными параметрами;
2. нелинейные системы с чистым запаздыванием;
К нелинейным системам относятся релейные системы.
По условиям функционирования :
· Стационарные – системы, параметры которых не изменяются во времени.
· Нестационарные.
Классификация по характеристикам управления
По принципу управления:
а) САУ с разомкнутой цепью воздействий. Разомкнутые системы можно разделить в свою очередь на два класса: системы, осуществляющие управление в соответствии с изменением только задающего воздействия и системы, управляющие при изменении возмущения.
Алгоритм управления разомкнутой системы первого типа имеет вид:
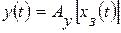
Чаще всего оператор Ау устанавливает пропорциональную связь между задающим воздействием хз( t ) и управляющим воздействием y ( t ), а сама система в этом случае осуществляет программное управление.
Достоинства: 1) простота, высокая надежность;
2) высокое быстродействие.
Недостатки: 1) отсутствие противодействия возмущению;
2) необходимость точной модели объекта.
Область применения системы: простые объекты, неподверженные существенным возмущениям с повышенными требованиями к надежности или быстродействию.
Система управления по возмущению – это такая система, в которой для уменьшения отклонения управляемой величины от заданной измеряется возмущающее воздействие, обрабатывается по определенному алгоритму и накладывается на прежний управляющий сигнал.
В системах управления по возмущению управляющее воздействие зависит от возмущающего и задающего воздействий:
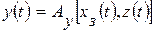
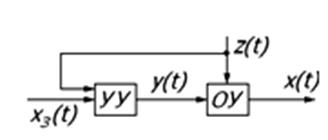
причем в большинстве случаев оператор Ау может быть разделен на две не зависящие друг от друга составляющие:
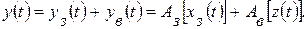
Оператор Аз соответствует, как правило, простому пропорциональному преобразованию сигнала хз( t ), а оператор Ав может быть и более сложным, например, устанавливающим нелинейное соотношение между сигналами ув( t ) и z ( t ).
В большинстве случаев разомкнутые системы управления по возмущению выполняют функции стабилизации управляемой величины.
Преимущество разомкнутых систем управления по возмущению – их быстродействие: они компенсируют влияние возмущения еще до того, как оно появится на выходе объекта. Но применимы эти системы лишь в том случае, если на управляемую величину действует одно или два возмущения и есть возможность измерения этих возмущений.
Достоинства: 1) возможность работы при наличии возмущений; 2) высокое быстродействие.
Недостатки: 1) относительная сложность; 2) необходимость точной модели объекта, в том числе по каналу возмущения.
Условия применения: 1) возможность измерения возмущающего воздействия; 2) наличие модели объекта по каналу возмущения.
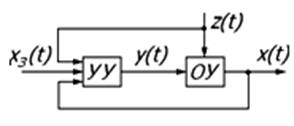
б) САУ с замкнутой цепью воздействий. Система управления по отклонению.
Управляющее воздействие в замкнутой системе формируется в большинстве случаев в зависимости от величины и знака отклонения истинного значения управляемой величины от ее заданного значения:
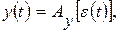
где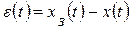 
- сигнал ошибки (называемый также сигналом рассогласования).
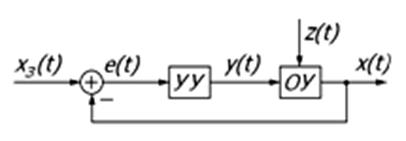
В замкнутой системе контролируется непосредственно управляемая величина и тем самым при выработке управляющих воздействий учитывается действие всех возмущений, влияющих на управляемую величину. В этом заключается преимущество замкнутых систем.
Но вначале возмущение должно проявиться на выходе, система «почувствует» отклонение и лишь потом выработает управляющие воздействия, направленные на устранение отклонения. Несмотря на наличие определенных недостатков, этот принцип широко применяют при создании автоматических систем.
Во всех замкнутых системах существуют обратные связи, которые подразделяются на жесткие обратные связи и гибкие обратные связи. Жесткие обратные связи – это такие связи, в которых обратный сигнал существует как в динамическом, так и в статическом режиме. Гибкие обратные связи – связи, в которых сигнал обратной связи существует только в динамическом режиме.
Достоинства: 1) уверенная работа при наличии существенных возмущений; 2) нет острой необходимости в точной модели объекта.
Недостатки: 1) относительная сложность; 2) сниженное быстродействие.
Область применения системы: почти любые объекты, кроме случаев невозможности измерения результата управления.
в) В комбинированных системах создают две цепи воздействий – по заданию и рассогласованию или по рассогласованию и возмущению, и управляющее воздействие формируется согласно оператору
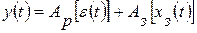или 
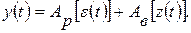
Эффективность работы комбинированной системы управления всегда больше, чем у порознь функционирующих замкнутой или разомкнутой систем.
По режимам функционирования
В зависимости от характера изменения задающего воздействия во времени автоматические системы управления разделяются на следующие классы:
а) Стабилизирующая автоматическая система управления (система стабилизации) – это система, алгоритм функционирования которой содержит предписание поддерживать значение управляемой величины постоянным:
б) Алгоритм функционирования программной автоматической системы содержит предписание изменять управляемую величину в соответствии с заранее заданной функцией времени f ( t ):
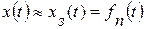
в) Следящая автоматическая система управления предназначена для изменения управляемой величины в соответствии с изменениями другой величины, которая действует на входе системы и закон изменения которой заранее не известен:
,
Следящие системы используют обычно для дистанционного управления перемещением объектов в пространстве.
По свойствам системы в установившемся режиме:
а) Статические системы - это такие системы, в которых управляемая величина в установившемся режиме зависит от величины возмущающего воздействия, в них при заданном воздействии, которое стремится к постоянному, отклонение управляемой величины также стремится к постоянной величине, отличной от нуля.
б) Астатические системы - это такие системы, в которых управляемая величина в установившемся режиме не зависит от величины возмущающего воздействия, в них отклонение управляемой величины при любом постоянном задающем воздействии стремится к нулю.
2.3 Классификация САУ по другим признакам
По усилению мощности сигнала:
а) САУ прямого действия- это такая САУ, в которой используется энергия управляемого объекта.
б) САУ непрямого действия - это САУ, в которых управляющий сигнал создаётся дополнительным усилительным устройством.
По количеству контуров в системе:
а) одноконтурныеСАУ – системы, в которых существует только одна главная обратная связь.
б) многоконтурныеСАУ – системы, в которых помимо обратной главной связи существуют местные обратные связи.
По связности системы:
а) односвязные САУ - это САУ, в которых присутствует либо один регулятор, либо несколько регуляторов, взаимодействие которых учитывается в законе управления.
б) многосвязные САУ - это САУ, в которых присутствует несколько регуляторов независимых друг от друга.
По размерности системы:
а) одномерные САУ – системы, в которых существует один управляющий сигнал и одна управляемая величина.
б) многомерные САУ – системы, в которых количество управляемых величин и управляющих сигналов превышает единицу
3. Функциональная и структурная схемы САУ
Упрощенное графическое изображение любой структуры автоматической системы, содержащее условное изображение ее частей, называют структурной схемой. Различаютфункциональные и алгоритмические структурные схемы.
Функциональные и алгоритмические схемы состоят из условных изображений элементов (звеньев) (обычно в виде прямоугольников) и различных связей, изображаемых в виде линий со стрелками, показывающих направление передачи воздействия. Каждая линия соответствует обычно одному сигналу или одному воздействию. Иногда применяют жирные или сдвоенные линии: в функциональных – для обозначения материальных и энергетических потоков, в алгоритмических - для обозначения векторных величин. Около каждой линии указывают физическую величину, характеризующую данное воздействие.
Обычно вначале составляют функциональную схему системы, а затем – алгоритмическую. Схемы могут быть составлены с большей или меньшей степенью детализации. Схемы, на которых показаны лишь главные или укрупненные части системы, называют обобщенными.
В большинстве случаев функциональная схема САУ содержит следующие основные устройства:
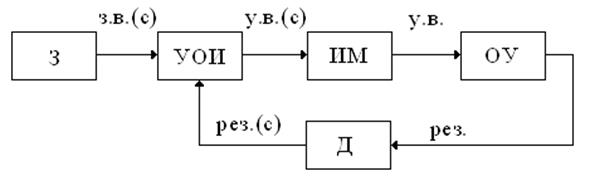
Устройство обработки информации (УОИ) – устройство, которое на основе анализа сигналов о желаемом и действительном результатом воздействия формирует управляющее воздействие в виде сигнала.
Исполнительный механизм (ИМ) – устройство, непосредственно воздействующее на объект управления с целью реализации управляющего воздействия.
Задатчик (З) – устройство, которое является источником информации о задании на управление, желаемом его результате.
Датчик (Д) – источник информации о фактическом результате управления.
Под структурной схемой САУ понимают обычно алгоритмическую. Алгоритмическая структурная схема в отличие от функциональной показывает математическое описание отдельных блоков и позволяет проводить математический анализ системы управления и синтез отдельных ее элементов.
Структурная схема линейной непрерывной САУ может включать в себя следующие элементы:
| № | Наименование элемента | Обозначение | Уравнение движения |
| 1. | Линейный блок/ Линейное звено |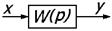 
| 
|
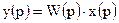
| 2. | Узел разветвления |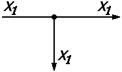 
| — |
| 3. | Сумматор |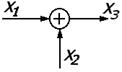 
| 
|
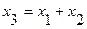
| 3а. | Элемент сравнения |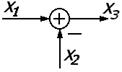 
| 
|
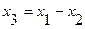
1) Линейный блок/линейное звено – элемент структурной схемы САУ, передающий на единственный выход сигнал с единственного входа, преобразованный в соответствии с передаточной функцией звена W(p).
2) Узел – элемент структурной схемы САУ, мгновенно передающий сигнал с единственного входа на все свои выходы.
3) Сумматор/элемент сравнения – элемент структурной схемы, мгновенно передающий на единственный выход сумму/разность сигналов на всех своих входах.
4. Статическая характеристика САУ
Режим работы САУ, в котором управляемая величина и все промежуточные величины не изменяются во времени, называется установившимся, или статическим режимом. Любое звено и САУ в целом в данном режиме описывается уравнениями статики вида y = F(u,f), в которых отсутствует время t. Соответствующие им графики называются статическими характеристиками. Статическая характеристика звена с одним входом u может быть представлена кривой y = F(u) . Если звено имеет второй вход по возмущению f, то статическая характеристика задается семейством кривых y = F(u) при различных значениях f, или y = F(f) при различных u.
Так примером одного из функциональных звеньев системы регулирования является рычаг. Уравнение статики для него имеет вид y = Ku. Его можно изобразить звеном, функцией которого является усиление (или ослабление) входного сигнала в K раз. Коэффициент K = y/u, равный отношению выходной величины к входной называется коэффициентом усиления звена. Когда входная и выходная величины имеют разную природу, его называют коэффициентом передачи.
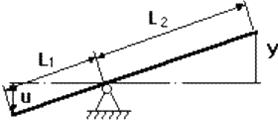
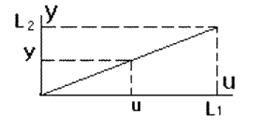
Статическая характеристика данного звена имеет вид отрезка прямой линии с наклоном a = arctg(L2/L1) = arctg(K) . Звенья с линейными статическими характеристиками называются линейными. Статические характеристики реальных звеньев, как правило, нелинейны. Такие звенья называются нелинейными. Для них характерна зависимость коэффициента передачи от величины входного сигнала: K = y/u ≠ const.
Например, статическая характеристика насыщенного генератора постоянного тока представлена на рисунке. Обычно нелинейная характеристика не может быть выражена какой-либо математической зависимостью и ее приходится задавать таблично или графически.
Зная статические характеристики отдельных звеньев, можно построить статическую характеристику САУ (см. рис.). Если все звенья САУ линейные, то САУ имеет линейную статическую характеристику и называется линейной. Если хотя бы одно звено нелинейное, то САУ нелинейная.
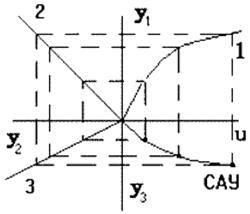
Звенья, для которых можно задать статическую характеристику в виде жесткой функциональной зависимости выходной величины от входной, называются статическими. Если такая связь отсутствует и каждому значению входной величины соответствует множество значений выходной величины, то такое звено называется астатическим. Примером астатического звена может служить двигатель, входной величиной которого является напряжение U, а выходной - угол поворота вала, величина которого при U = const может принимать любые значения. Выходная величина астатического звена даже в установившемся режиме является функцией времени.
5. Уравнение движения и передаточная функция
Система автоматического управления может быть полностью описана дифференциальным уравнением, т.н. уравнением движения, устанавливающим связь между входной и выходной величинами как в переходных, так и в установившихся режимах:
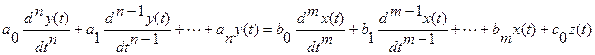
где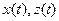 
- входные величины элемента, 
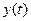- выходная величина элемента, 
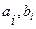- коэффициенты уравнения, называемые параметрами.
Уравнение движения может быть записано в более короткой символической (операторной) форме. Переход к этой форме осуществляют введением сокращенного условного обозначения операции дифференцирования: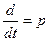 
, где p – дифференциальный оператор. Соответственно k-тую производную обозначают 
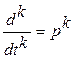. Тогда исходное уравнение можно записать в виде:
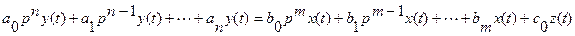
или:
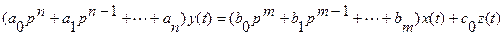
Введем обозначения: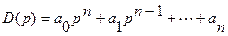 
– дифференциальный оператор при выходной величине, наз. собственным, или характеристическим оператором. Название обусловлено тем, что многочлен характеризует собственное движение элемента, т.е. движение при отсутствии внешних воздействи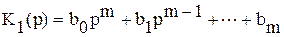й. 
и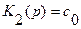 
– дифференциальные операторы при входных величинах, наз. операторами воздействия, операторами входа. Тогда
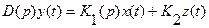
Другая форма записи дифференциальных уравнений основана на применении преобразования Лапласа. Применим преобразование Лапласа к дифференциальному уравнению, считая, что до приложения внешнего воздействия система находилась в покое и все начальные условия равны нулю. Получим:
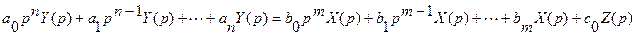
Сравнивая с уравнением в символической форме, замечаем их полную аналогию. Разница только в значении символа р: в одном случае это операция дифференцирования, в другом – комплексное число.
Передаточной функцией W( p) называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях:
Передаточная функция также равна отношению входного оператора к собственному оператору:
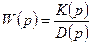
Как видно, передаточная функция представляет собой некоторый динамический оператор, характеризующий прохождение сигналов через линейный элемент.
Часто рассматривают передаточную функцию по управлению
и передаточную функцию по возмущению
Для реальных элементов, описываемых обыкновенными дифференциальными уравнениями, передаточная функция представляет собой правильную рациональную дробь
у которой степень многочлена числителя меньше или равна степени многочлена знаменателя, т.е.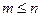 
. Все коэффициенты передаточной функции – действительные числа, характеризующие параметры элемента.
Для элементов, описываемых передаточной функцией невысокого порядка (n < 3), принято записывать передаточную функцию в стандартной форме. При этом передаточную функцию преобразовывают таким образом, чтобы свободный член знаменателя 
был равен единице. При этом свободный член числителя 
становится равным передаточному коэффициенту и его выносят за скобки:
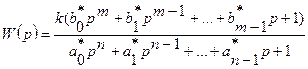, где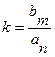 
Передаточная функция является функцией комплексной переменной 
, которая может при некоторых значениях переменной р обращаться в ноль или бесконечность. Значение переменной р, при котором передаточная функция обращается в ноль, называют нулём, а значение, при котором обращается в бесконечность – полюсом передаточной функции. Очевидно, что нулями передаточной функции являются корни полинома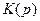 
, а полюсами - корни полинома 
.
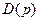6. Типовые воздействия и временные характеристики САУ
Классификация динамических звеньев производится по виду дифференциального уравнения, описывающего поведение звена в динамических режимах работы САУ. Однако вид дифференциального уравнения не является единственным признаком, по которому проводится сравнение динамических звеньев. Для этого используются следующие характеристики:
· Дифференциальные уравнения движения динамического звена.
· Передаточные функции W(p);
· Временные характеристики, к которым относятся:
o переходная функция или переходная характеристика h(t),
o импульсная передаточная функция или функция веса w(t),
· Частотные характеристики, к которым относятся:
o амплитудно-частотные характеристики, в т.ч. логарифмические,
o фазочастотные характеристики, в т.ч. логарифмические,
o амлитудно-фазовые частотные характеристики.
Дифференциальные уравнения движения динамического звена и его передаточные функции рассмотрены в предыдущем разделе.
Временные характеристики определяют вид изменения выходного сигнала при подаче на вход звена типового управляющего воздействия. Это позволяет сравнивать свойства звеньев в динамических режимах работы. Временные свойства звена определяются его переходной и импульсной переходной характеристиками.
Переходная функция или переходная характеристика h ( t ) представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равного единице. Такое воздействие называется единичной ступенчатой функцией и обозначается
X(t) = 1(t),
что соответствует следующим условиям:
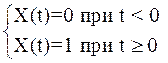
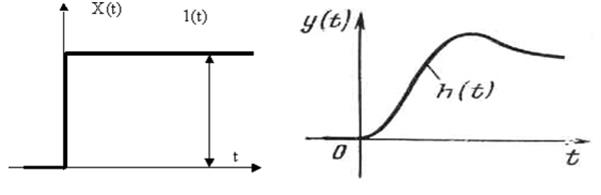
Изображение единичной ступенчатой функции определяется как
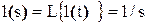
Чтобы определить изображение переходной функции при известной передаточной функции звена W(s) необходимо выполнить следующую операцию:
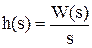
Ступенчатая функция представляет собой распространенный вид входного воздействия в САУ. К такому виду воздействия сводятся возрастание момента на валу двигателя, мгновенное изменение задания на частоту вращения двигателя.
Функция веса или импульсная переходная характеристика представляет собой реакцию звена на единичную импульсную функцию. Единичная импульсная функция, или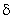 
-функция, представляет собой производную от единичной ступенчатой функции. То есть
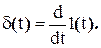
Дельта-функция тождественно равна нулю во всех точках, кроме t=0, где она стремится к бесконечности.
Основное свойство дельта-функции состоит в том, что
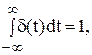
то есть она имеет единичную площадь.
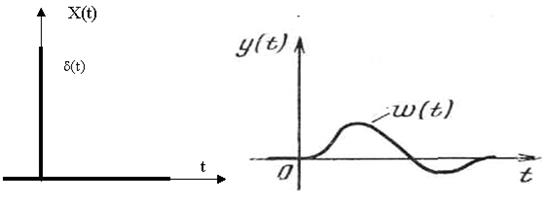
Нетрудно установить, что изображение дельта-функции определяется как
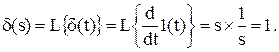
Изображение функции веса определяется как:
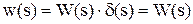
Очевидно, что изображение импульсной переходной характеристики совпадает с передаточной функцией звена или САУ.
Зная переходную или весовую функцию САУ, можно определить реакцию системы на произвольное входное воздействие при нулевых начальных условиях с помощью следующих формул:
, 
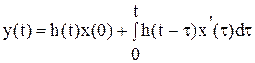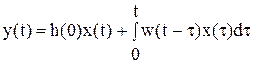
Две рассмотренные формулы легко получаются друг из друга, являясь вариантами интеграла Дюамеля, или интеграла свертки. Для реальных инерционных звеньев реакция на выходе всегда отстает от входного воздействия, т.е.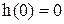 
.
7. Частотные характеристики САУ
Частотные характеристики описывают передаточные свойства элементов и систем в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Зная частотную характеристику элемента, можно определить реакцию элемента на гармоническое воздействие любой частоты, а также на сумму гармонических воздействий различной частоты. Частотные характеристики широко используются в теории и практике автоматического управления, так как реальные возмущения, действующие на автоматические системы, могут быть представлены как сумма гармонических сигналов.
Пусть на вход линейного элемента в момент времени t = 0 подано гармоническое воздействие определенной частоты w.
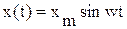
Через некоторое время, необходимое для протекания переходного процесса, элемент войдет в режим установившихся вынужденных колебаний, а выходная величина y ( t ) будет изменяться по гармоническому закону с той же частотой w , но с отличающейся амплитудой ym и со сдвигом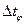 
по оси времени
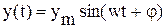
где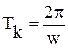 
– период колебаний; 
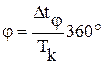– фазовый сдвиг между входным и выходным сигналами.
Повторяя такой эксперимент при фиксированном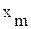 
для различных значений частоты (от 0 до 
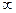), можно установить, что амплитуда 
и фазовый сдвиг 
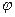выходного сигнала конкретного элемента зависят от частоты воздействия.
Подавая гармоническое воздействие на вход различных элементов, можно убедиться, что величины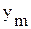 
и 
зависят также от типа и параметров элемента.
Так как амплитуда выходного сигнала зависит ещё от амплитуды входного сигнала, то целесообразно при описании передаточных свойств элементов рассматривать отношение амплитуд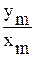 
.
Зависимость отношения амплитуд выходного и входного сигнала от частоты называют амплитудной частотной характеристикой (сокращенно - АЧХ) и обозначают А( w ) (см. рис. а). Зависимость фазового сдвига между входным и выходным сигналами от частоты называют фазовой частотной характеристикой (ФЧХ) и обозначают j ( w ) (см. рис. б). Аналитические выражения А( w ) и j ( w ) называют соответственно амплитудной и фазовой частотными функциями.
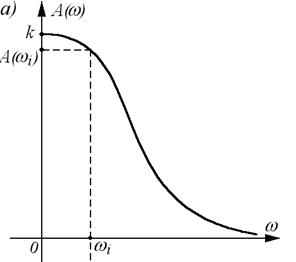
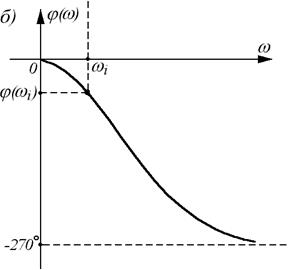
АЧХ показывает, как элемент пропускает сигналы различной частоты. Оценка пропускания производится по отношению амплитуд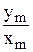 
в установившемся режиме. АЧХ имеет размерность, равную отношению размерности выходной величины к размерности входной. ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах в установившемся режиме.
Амплитудную и фазовую частотные характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ или АФХ). Амплитудно-фазовая частотная характеристикаW ( j w ) представляет собой функцию комплексного переменного j w, модуль которой равен А( w ), а аргумент равен j ( w ). Каждому фиксированному значению частоты w i соответствует комплексное число W ( j w i ), которое на комплексной плоскости можно изобразить вектором, имеющим длину А( w i ) и угол поворота j ( w i ) (см. рис. в). Отрицательные значения j ( w ), соответствующие отставанию выходного сигнала от входного, принято отсчитывать по часовой стрелке от положительного направления действительной оси.
При изменении частоты от нуля до бесконечности вектор W ( j w ) поворачивается вокруг начала координат, при этом одновременно увеличивается или уменьшается длина вектора. Кривая, которую при этом опишет конец вектора, называемая годографом, и есть АФЧХ. Каждой точке характеристики соответствует определенное значение частоты.
Проекции вектора W ( j w ) на действительную и мнимую оси называют соответственно действительной и мнимой частотными характеристиками и обозначают
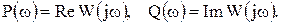
При этом, действительная частотная характеристика Р( w ) – всегда четная, а мнимая характеристика Q ( w ) – всегда нечетная функции частоты.
Аналитическое выражение для АФЧХ конкретного элемента можно получить из его передаточной функции путем подстановки р= j w:
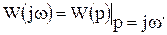
АФЧХ W ( j w ), как и любая комплексная величина, может быть представлена в показательной форме
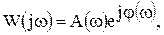
где А( w ) – модуль АФЧХ, а j ( w ) – угол сдвига по фазе; алгебраической
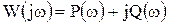
или тригонометрической
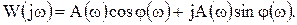
Связь между различными частотными функциями следующая:
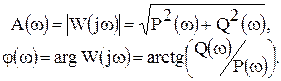
Выделение действительной и мнимой составляющих частотной передаточной функции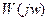 
возможно с помощью следующих формул:
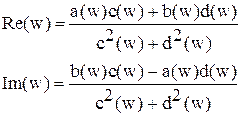
где a ( w ) – действительная часть числителя функции W ( jw ), b ( w ) – мнимая часть числителя, c ( w ) – действительная часть знаменателя, d ( w ) – мнимая часть знаменателя
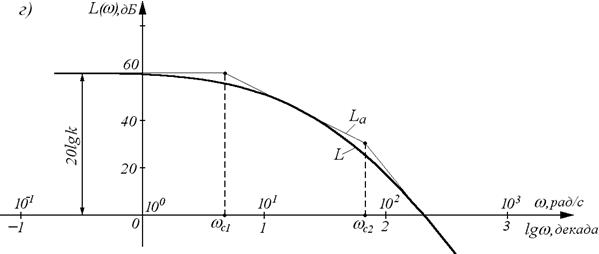
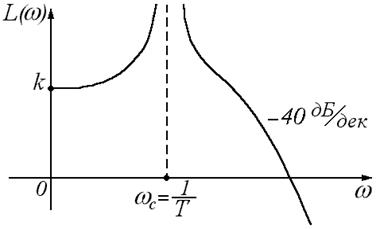
При практических расчетах автоматических систем удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков.
За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением w i и его десятикратным значением 10w i. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1. При построении ЛЧХ по оси абсцисс откладывают логарифм частоты, а подписывают соответствующие значения частот. Ось ординат проводят через произвольную точку.
Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)
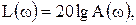
ординаты которой измеряют в логарифмических единицах – белах (Б) или децибелах (дБ).
При построении фазовой частотной характеристики логарифмический масштаб применяют только для оси абсцисс.
На рис. г показаны ЛАЧХ L( w ) (толстая линия) и соответствующая ей приближенная (асимптотическая) характеристика Lа( w ) в виде прямолинейных отрезков (тонкая линия). Частоты, соответствующие точкам стыковки отрезков, называют сопрягающими и обозначают w с.
8. Позиционные звенья САУ
8.1 Безынерционное звено
Является простейшим среди всех типовых звеньев, безынерционное звено передает сигнал со входа на выход мгновенно, без искажения его формы. В звене может происходить только усиление или ослабление мгновенных значений входной величины. Связь между мгновенными значениями входной и выходной величин описываются алгебраическим уравнением движения
;
k – коэффициент усиления или передачи звена характеризует наклон статической характеристики.
Уравнение движения звена в операторной форме
,
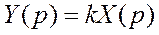отсюда передаточная функция
.
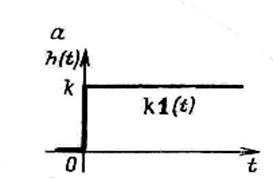
При единичном ступенчатом воздействии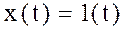 
, приложенном в момент времени t = 0, выходная величина мгновенно изменяется и принимает значение k. Переходная функция звена (см. рис. а) имеет вид
.
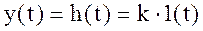Аналогично, функция веса (рис. б) определяется выражением
.
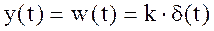Сигналы любой частоты (от нуля до бесконечности) проходят через безынерционное звено с одинаковым отношением амплитуд выходной и входной величин, равным k.
Примерами технической реализации звена являются механический редуктор, потенциометрический датчик углового перемещения, тахогенератор, операционный усилитель.
Понятие безынерционного звена является продуктом математической идеализации. На самом деле все реальные конструктивные элементы обладают некоторой инерционностью, так как передача энергии со входа на выход не может осуществляться мгновенно.
8.2 Апериодическое (инерционное) звено I-го порядка
Дифференциальное уравнение апериодического звена имеет вид
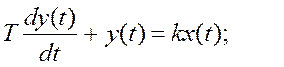
передаточная функция
,
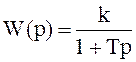переходная функция (рис. а)
,
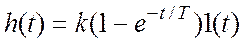функция веса (рис. б)
.
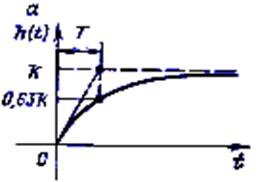
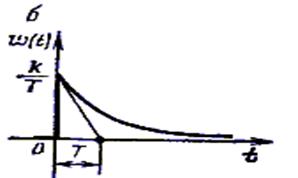
T – постоянная времени – отрезок, отсекаемый на асимптоте касательной, проведенной к кривой в любой точке. Чем больше Т, тем дольше длится переходный процесс. Практически переходный процесс считается законченным через tп = 3Т. Постоянная времени характеризует инерционность апериодического звена.
Амплитудно-фазовая частотная характеристика определяется заменой p на jw в W(p):
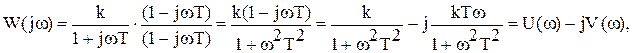
где 
– мнимая часть АФЧХ.
Если из действительной части U(w) определить w и подставить в мнимую часть V(w), то после некоторых элементарных преобразований получим уравнение амплитудно-фазовой частотной характеристики (см. рис.) в декартовых координатах U(w) и V(w) в виде уравнения окружности с центром в точке (k/2; 0):
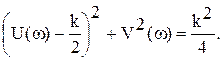
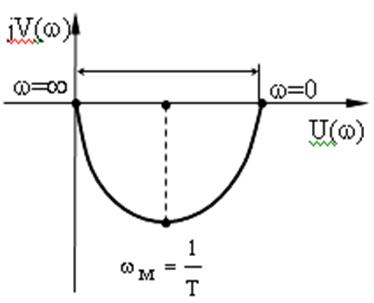
Инерционными звеньями первого порядка являются конструктивные элементы, которые могут накапливать и передавать энергию или вещество. В электрических элементах накопителем энергии электрического поля служит конденсатор, а магнитного – индуктивность. В механических элементах потенциальная энергия накапливается в пружинах и других упругих элементах, а кинетическая – в движущихся массах. Простейшим примером такого элемента является электрический пассивный четырехполюсник (см. рис.). Выходная величина после подачи на его вход постоянного напряжения u1 изменяется пропорционально величине накапливаемого в емкости заряда. В первый момент времени заряд растет быстро, а затем по мере приближения напряжения u2 к входному напряжению, ток заряда становится все меньше, и скорость возрастания напряжения u2 постепенно падает до нуля.
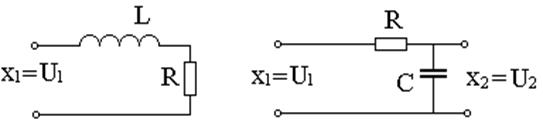
Более сложным примером звена такого рода служит электрический генератор постоянного тока, у которого входной величиной является напряжение возбуждения, а выходной величиной – ЭДС, наводимая в обмотке якоря генератора.
8.3 Позиционные звенья II порядка
Динамика процессов звене II порядка описывается уравнением:
,
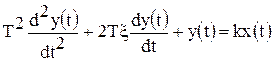где k - коэффициент усиления звена; Т - постоянная времени колебательного звена;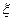 
- коэффициент демпфирования звена (или коэффициент затухания).
В зависимости от величины коэффициента демпфирования различают четыре типа звеньев:
а) колебательное 0<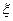 
<1;
б) апериодическое звено II порядка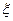 
>1;
в) консервативное звено 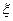=0;
г) неустойчивое колебательное звено 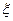<0.
Переходные характеристики различных звеньев II порядка:
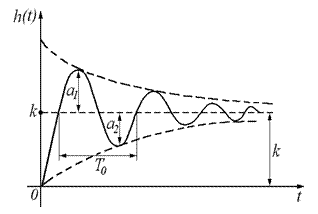
Амплитуды первых двух колебаний определяют величину 
, или её можно найти, определив постоянную времени экспоненты, с которой происходит затухание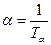 
.
Чем ближе коэффициент затухания к единице, тем меньше амплитуда колебаний, чем меньше Т, тем быстрее устанавливаются переходные процессы.
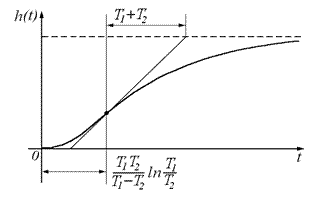
Апериодическое звено II порядка не является элементарным, поскольку представляет собойпоследовательное соединение двух апериодических звеньев I порядка с постоянными времени Т1 и Т2.
|
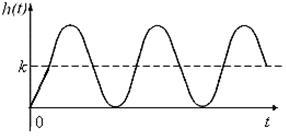
или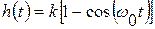 
.
Здесь w 0 – величина, обратная постоянной времени (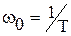 
); 
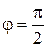
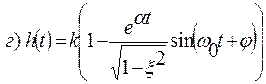
Все переходные характеристики колеблются вдоль величины k.
2. Импульсные переходные характеристики звеньев II порядка:
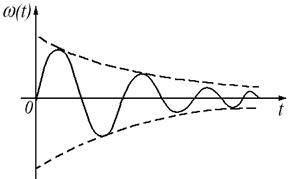
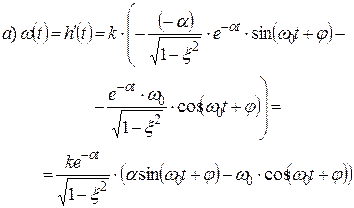
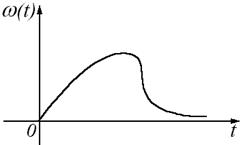
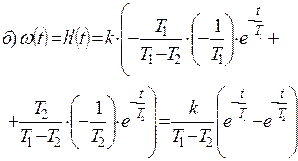
3. Передаточные функции звеньев II порядка:
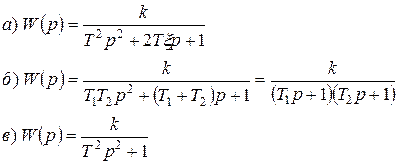
4. АФЧХ:
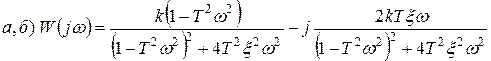
График АФЧХ будет выглядеть следующим образом: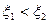 
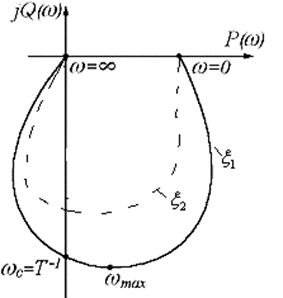
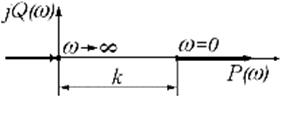Для апериодического звена - 
.
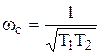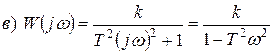
5. АЧХ:
.
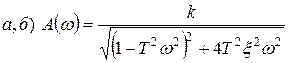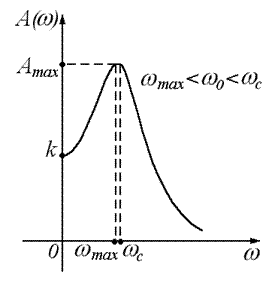На частоте 
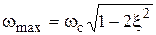АЧХ колебательного звена имеет максимум (резонансный пик), равный
.
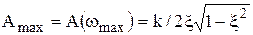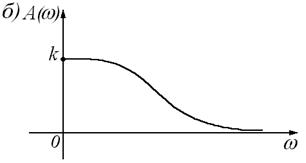Отсюда видно, что чем меньше коэффициент x, тем больше резонансный пик.
По графику АЧХ видно, что колебательное звено, как и все инерционные звенья, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты; если частота гармонического входного сигнала близка к частоте собственных колебаний звена, то отношение амплитуды выходного сигнала к амплитуде входного больше передаточного коэффициента k.
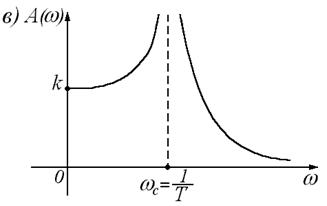
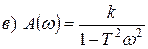
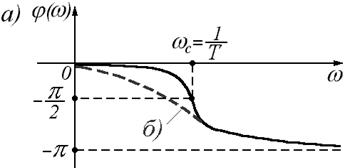6. ФЧХ:
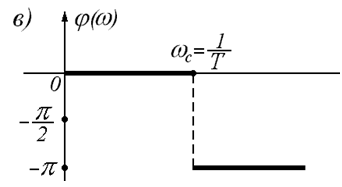
Для случая б) график будет аналогичным, только перегиб будет чуть меньше (штриховая линия на графике).
7. ЛАЧХ:
а,б) 
, где 
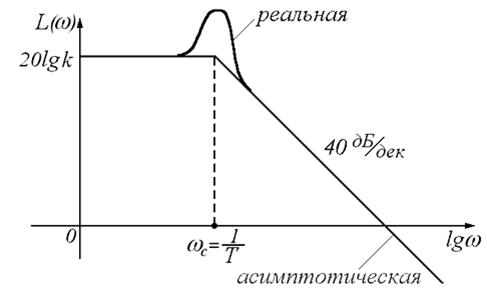
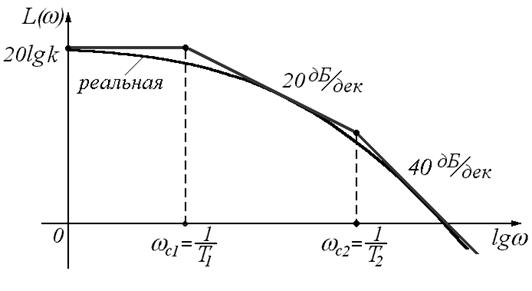
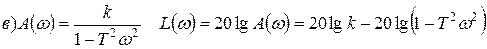
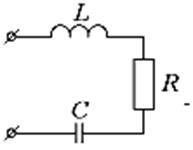
Примером звена II порядка (колебательного) является RLС- цепь.
9. Непозиционные звенья САУ
9.1 Интегрирующие звенья
Различают два вида интегрирующих звеньев: идеальные и реальные. Общей особенностью интегрирующих звеньев является пропорциональность производной выходной величины мгновенному значению входной величины.
Дифференциальное уравнение идеального интегрирующего звена
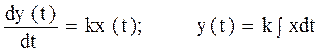
Передаточная функция идеального интегрирующего звена
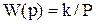
Скорость изменения выходной величины пропорциональна входной величине. Подставляя в уравнение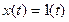 
, получим переходную функцию
,
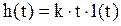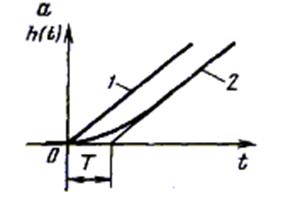
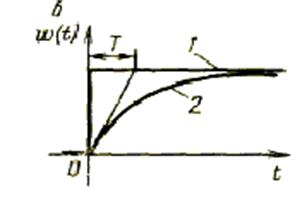
график которой показан на рис а, кривая 1.
Аналогично получим функцию веса (рис. б, кривая 1)
,
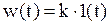Дифференциальное уравнение реального интегрирующего звена
,
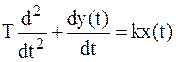а передаточная функция
.
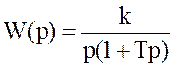Такое звено может рассматриваться как последовательное соединение двух звеньев – идеального интегрирующего и апериодического 1-го порядка.
Переходная и весовая характеристики реального интегрирующего звена приведены соответственно на рис. а (кривая 2) и б (кривая 2).
Интегрирующие свойства присущи всем объектам управления, в которых происходит накопление вещества или энергии без ее одновременной отдачи в окружающую среду. Классическим примером объекта с интегрирующими свойствами является резервуар с жидкостью, если в качестве входной переменной рассматривать подачу жидкости, а выходной – уровень жидкости.
Интегрирующими звеньями являются различные исполнительные двигатели и механизмы – устройства, которые перемещают регулирующие органы (шиберы, заслонки и т.д.). Входной величиной этих устройств служит обычно количество энергии или вещества, поступающих в устройство, а выходной – линейное или угловое перемещение какого-либо элемента. Примерами могут служить гидравлический исполнительный механизм, электрические исполнительные двигатели постоянного и переменного тока, например, двухфазный асинхронный двигатель.
Общие свойства интегрирующих звеньев:
1. После подачи ступенчатого входного воздействия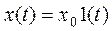 
выходная переменная y(t) неограниченно возрастает и по окончании переходного процесса изменяется по линейному закону 
При снятии входного воздействия выходная переменная сохраняет достигнутое значение, поэтому интегрирующие звенья можно использовать в качестве запоминающих элементов (элементов с памятью).
2. В передаточную функцию обязательно входит сомножитель 1/p, поэтому
.
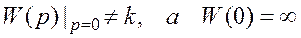3. Интегрируюшие звенья, как и инерционные статические, являются фильтрами низкой частоты; в режиме гармонических колебаний они вносят отрицательные фазовые сдвиги.
9.2 Дифференцирующие звенья
Дифференцирующие звенья могут быть идеальными (безынерционными) и реальными (инерционными). Мгновенное значение выходной величины идеального дифференцирующего звена пропорционально в каждый момент времени производной входной величины:
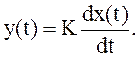
Передаточная функция звена
.
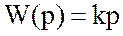Переходная функция звена получается непосредственно из этого уравнения подстановкой и дифференцированием единичной ступенчатой функции
.
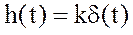Импульсная переходная функция
.
Графики переходной и весовой функций показаны соответственно на рис. а (кривая 1) и б (кривая 1).
Реальное дифференцирующее звено представляет собой последовательное соединение идеального дифференцирующего звена и инерционного звена первого порядка. Его уравнение
,
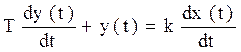а передаточная функция
.
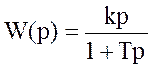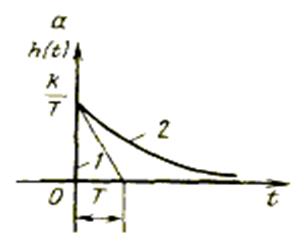
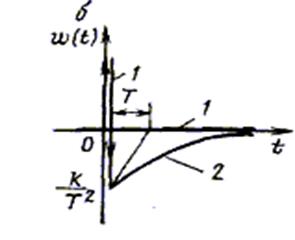
Временные характеристики реального дифференцирующего звена показаны на рис. а (кривая 2) и б (кривая 2).
Идеальным (R=0) и реальным (R¹0) дифференцирующим звеном является электрическая цепь
Общие свойства дифференцирующих звеньев:
1. При подаче на вход звена ступенчатого воздействия на его выходе возникает большой кратковременный импульс, а затем по окончании переходного процесса выходная переменная становится равной нулю. Если входной сигнал не изменяется во времени, то выходной равен нулю. Если же входной сигнал x(t) возрастает по линейному закону x(t)=a1 t, то выходной
.
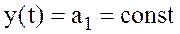2. В передаточную функцию всегда входит множитель p , поэтому
.
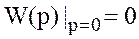3. Дифференцирующие звенья являются фильтрами высокой частоты, т.е. хорошо пропускают высокочастотные сигналы и плохо – низкочастотные. Они вносят положительные фазовые сдвиги.
10. Типовые соединения звеньев в структурных схемах САУ
Для упрощения (свертывания) сложных алгоритмических схем применяют три главных правила преобразования, с помощью которых определяют эквивалентные передаточные функции типовых соединений звеньев:
v Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций всех звеньев, входящих в соединение.
Определим передаточную функцию последовательного соединения.
v Передаточная функция параллельно соединенных звеньев равна алгебраической сумме передаточных функций всех звеньев, входящих в соединение.
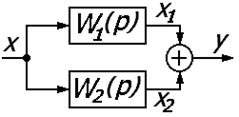
v Передаточная функция встречно-параллельного соединения с отрицательной (положительной) обратной связью равна передаточной функции прямой цепи, деленной на единицу плюс (минус) произведение передаточных функций прямой цепи и цепи обратной связи.
Соединение звеньев с отрицательной обратной связью.
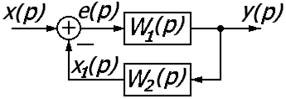
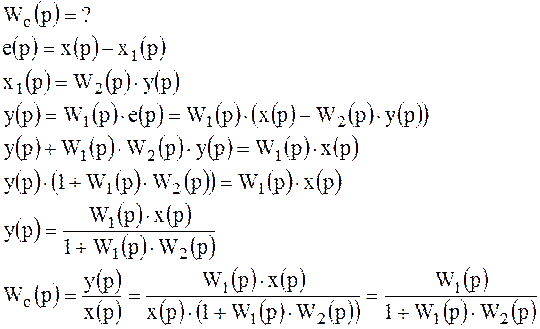
Аналогично для встречно-параллельного соединения звеньев с отрицательной обратной связью
С помощью этих правил удается преобразовать любую исходную алгоритмическую схему, не содержащую перекрестных связей, к одноконтурной схеме.
11. Правила эквивалентного преобразования
структурных схем
В случае если перекрестные связи в исходной схеме имеются, перед выделением типовых соединений необходимо избавиться от таких связей с помощью приведенных ниже правил.
| № | Название правила | Схемы до и после преобразования |
| 1 | Перенос сумматоров |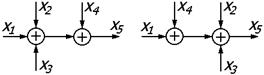 
|
| 2 | Перестановка звеньев |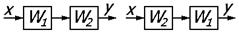 
|
| 3 | Перенос узла с выхода сумматора на вход |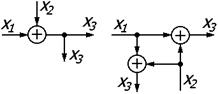 
|
| 4 | Перенос узла с входа сумматора на выход |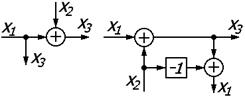 
|
| 5 | Перенос узла с выхода звена на вход |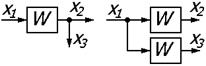 
|
| 6 | Перенос узла со входа звена на выход |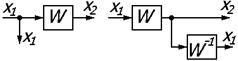 
|
| 7 | Перенос сумматора с выхода звена на вход |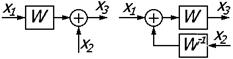 
|
| 8 | Перенос сумматора со входа звена на выход |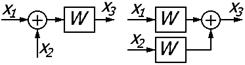 
|
| 9 | Замена передаточных функций прямой и обратной цепи |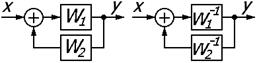 
|
| 10 | Приведение к единичной обратной связи | 
|
12. Передаточные функции замкнутой системы
Для замкнутой системы с единичной отрицательной обратной связью справедливо следующее уравнение замыкания:
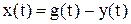
Решая передаточную функцию разомкнутой системы и уравнение замыкания, получаем следующее выражение
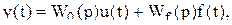
для ошибки
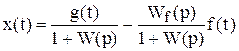
Выражение
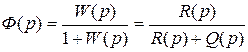
называется передаточной функцией замкнутой системыили главным оператором. Передаточная функция замкнутой системы показывает связь между регулируемой величиной и задающим воздействием при равенстве нулю возмущающих воздействий:
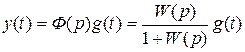
Выражение:
называют передаточной функцией замкнутой системы по ошибке. Оно показывает связь между ошибкой и задающим воздействием в замкнутой системе при равенстве нулю возмущающих воздействий:
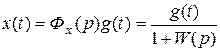
13. Устойчивость САУ. Правило Ляпунова
Устойчивость автоматической системы – это свойство системы возвращаться в исходное состояние равновесия после прекращения воздействия, выведшего систему из этого состояния. Неустойчивая система не возвращается в исходное состояние, а непрерывно удаляется от него.
Точная и строгая теория управления систем, описываемых обыкновенными дифференциальными уравнениями, создана А.М. Ляпуновым в 1892.
 |
Здесь, в рисунке а), А0 – невозмущенное состояние, А2 – возмущенное состояние; на рисунке б) изображено неустойчивое состояние системы, а на рисунке в) – ее нейтральное состояние. По аналогии с состояниями можно ввести понятие возмущенного и невозмущенного движения.
Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением
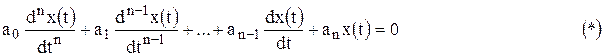
где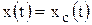 
- свободная составляющая выходной величины системы.
Система является устойчивой, если свободная составляющая xc ( t ) переходного процесса с течением времени стремится к нулю, т.е. если
.
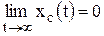Если свободная составляющая неограниченно возрастает, т.е. если
,
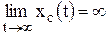то система неустойчива.
Наконец, если свободная составляющая не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости.
Найдем общее условие, при котором система, описываемая уравнением (*), устойчива. Решение уравнения (*) равно сумме
где Ck – постоянные, зависящие от начальных условий; pk – корни характеристического уравнения
.
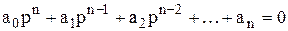Корни данного уравнения могут быть действительными (pk = a k), мнимыми (pk = j b k) и комплексными (pk = a k ± j b k).
Переходная составляющая (**) при t®¥ стремится к нулю лишь в том случае, если каждое слагаемое вида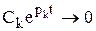 
. Характер этой функции времени зависит от вида корня pk. Рассмотрим все возможные случаи расположения корней pk на комплексной плоскости (см. рис.) и соответствующие им функции xk ( t ), которые показаны внутри кругов (как на экране осциллографа).
1. Каждому действительному корню pk = a k в решении (**) соответствует слагаемое вида
Если a k<0 (корень р1), то функция (***) при t®¥ стремится к нулю. Если a k>0 (корень р3), то функция (***) неограниченно возрастает. Если a k=0 (корень р2), то функция (***) остается постоянной.
2. Каждой паре сопряженных комплексных корней pk = a k ± j b k в решении (**) соответствуют два слагаемых, объединенных в одно
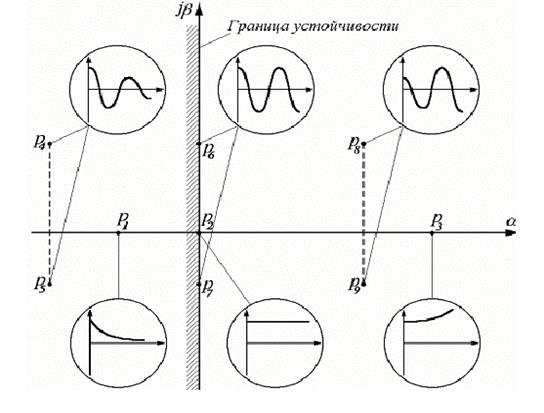
Эта функция представляет собой синусоиду с частотой b k и амплитудой, изменяющейся во времени по экспоненте. Если действительная часть двух комплексных корней a k<0 (корни р4 и р5), то колебательная составляющая (****) будет затухать. Если a k>0 (корни р8 и р9), то амплитуда колебаний будет неограниченно возрастать. Наконец, если a k=0 (корни р6 и р7), т.е. если оба сопряженных корня – мнимые (pk =+ j b k , pk +1 =- j b k), то xk ( t ) представляет собой незатухающую синусоиду с частотой b k.
Общее условие устойчивости (Правило Ляпунова):
Для устойчивости линейной автоматической системы управления необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательны.
При этом действительные корни рассматриваются как частный случай комплексных корней, у которых мнимая часть равна нулю. Если хотя бы один корень имеет положительную действительную часть, то система будет неустойчивой.
Устойчивость системы зависит только от вида корней характеристического уравнения и не зависит от характера внешних воздействий на систему. Устойчивость есть внутреннее свойство системы, присущее ей вне зависимости от внешних условий.
Используя геометрическое представление корней на комплексной плоскости (см. рис.) в виде векторов или точек, можно дать вторую формулировку общего условия устойчивости(эквивалентную основной):
Для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости. Если хотя бы один корень находится в правой полуплоскости, то система будет неустойчивой.
Мнимая ось j b является границей устойчивости в плоскости корней. Если характеристическое уравнение имеет одну пару чисто мнимых корней (pk =+ j b k , pk +1 =- j b k), а все остальные корни находятся в левой полуплоскости, то в системе устанавливаются незатухающие гармонические колебания с круговой частотой 
. В этом случае говорят, что система находится на колебательной границе устойчивости.
Точка b =0 на мнимой оси соответствует так называемому нулевому корню. Если уравнение имеет один нулевой корень, то система находится на апериодической границе устойчивости. Если таких корня два, то система неустойчива.
14. Алгебраический критерий Гурвица
Основной недостаток правила Ляпунова, затрудняющий его непосредственное применение, заключается в необходимости поиска корней характеристического полинома. Существуют различные критерии (условия), позволяющие судить о знаках корней характеристического уравнения по его коэффициентам, не решая это уравнение.
Автоматическая система, описываемая характеристическим уравнением
,
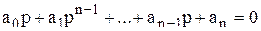устойчива, если при a 0>0 положительны все определители ∆1, ∆2, . . .∆п вида
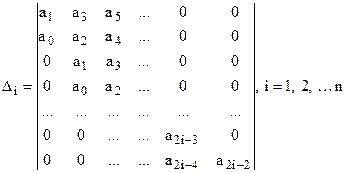
Если хотя бы один из определителей, называемых определителями Гурвица, отрицателен, то система неустойчива. Если главный определитель ∆п=0, а все остальные определители неотрицательны, то система находится на границе устойчивости.
Сформулируем необходимое условие устойчивости:
Для устойчивости линейной непрерывной САУ необходимо (но не всегда достаточно!), чтобы все коэффициенты ее характеристического полинома были положительны (одного знака).
Рассмотрим частные случаи применения критерия Гурвица для n=1;2;3;4. Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить следующие условия.
1. Для уравнения первого порядка (n=1)
условие устойчивости: а0>0 и ∆1=а1>0, т.е. для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.
2. Для уравнения второго порядка (n=2)
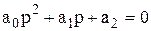
условие устойчивости:
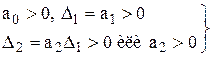
Т.о., и для системы второго порядка необходимое условие устойчивости (положительность коэффициентов) является одновременно и достаточным.
3. Для уравнения третьего порядка (n=3)
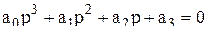
условие устойчивости:
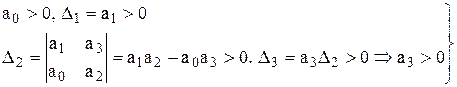
При n=3 для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля и произведение средних коэффициентов уравнения (а1, а2) было больше произведения крайних (а0, а3).
4. Для уравнения четвертого порядка (n=4)
кроме положительности всех коэффициентов требуется выполнение условия
.
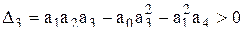При n=4 система будет устойчива при всех коэффициентах больших нуля и при
.
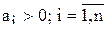Т.о., для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель ∆п-1 были положительными.
15. Критерий устойчивости Рауса
Этот критерий устойчивости был в 1877 г. предложен английским математиком и механиком Э. Раусом в виде некоторого правила (алгоритма), которое наиболее просто поясняет таблица.
В первой строке таблицы записывают в порядке возрастания индексов коэффициенты характеристического уравнения, имеющие четный индекс; во второй строке — коэффициенты с нечетным индексом. Любой из остальных коэффициентов таблицы определяют как
, 
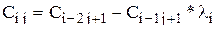В выражениях: j — индекс, означающий номер столбца таблицы; i – индекс, означающий номер строки таблицы.
| C00=a0 | C01=a2 | C02=a4 | C03=a6 | … | |
| C10=a1 | C11=a3 | C12=a5 | C13=a7 | … | |
| 
| 
| 
| … | … |
| 
| 
| 
| … | … |
| 
| 
| 
| … | … |
| 
| 
| 
| … | … |
| … | … | … | … | … | … |
| … | … | … | … | … | … |
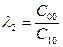
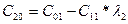
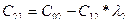
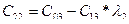
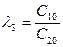
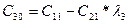
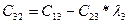
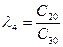
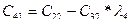
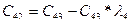
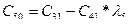
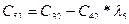
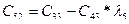
Заметим, что число строк таблицы Рауса равно степени характеристического уравнения плюс единица.
После того как таблица Рауса заполнена, по ней можно сделать суждение об устойчивости системы. Условие устойчивости Рауса формулируется так: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т. е.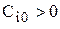 
Если не все коэффициенты первого столбца положительны, то система неустойчива, а число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса.
16. Критерий устойчивости Михайлова
Пусть левая часть уравнения движения, называемая характеристическим полиномом, имеет вид
Подставим в этот полином вместо переменного р чисто мнимый корень, который в дальнейшем будем обозначать jw. Тогда получим функцию комплексного переменного
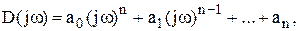
которую можно представить в виде суммы действительной и мнимой частей:
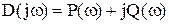
Действительная часть Р (ω) содержит только четные степени переменного ω
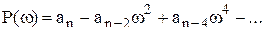
а мнимая часть — только нечетные
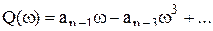
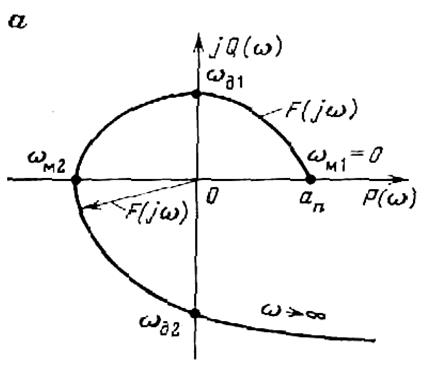
Каждому фиксированному значению переменного ω соответствует комплексное число, которое можно изобразить в виде вектора на комплексной плоскости. Если теперь изменять параметр (ω от 0 до ∞, то конец вектора D (jω) опишет некоторую линию (рис. а), которая называется характеристической кривой или годографом Михайлова. По виду этой кривой можно судить об устойчивости системы.
Дата добавления: 2019-09-13; просмотров: 254; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!