Свойства индексов разносторонности

Первые два утверждения связывают стороны треугольника с его индексами разносторонности.

Предложение 1. Стороны треугольника и его индексы разносторонности связаны формулами

Доказательство. Для всех сторон треугольника запишем теорему о делении этой стороны биссектрисой противолежащего угла (рис. 34).

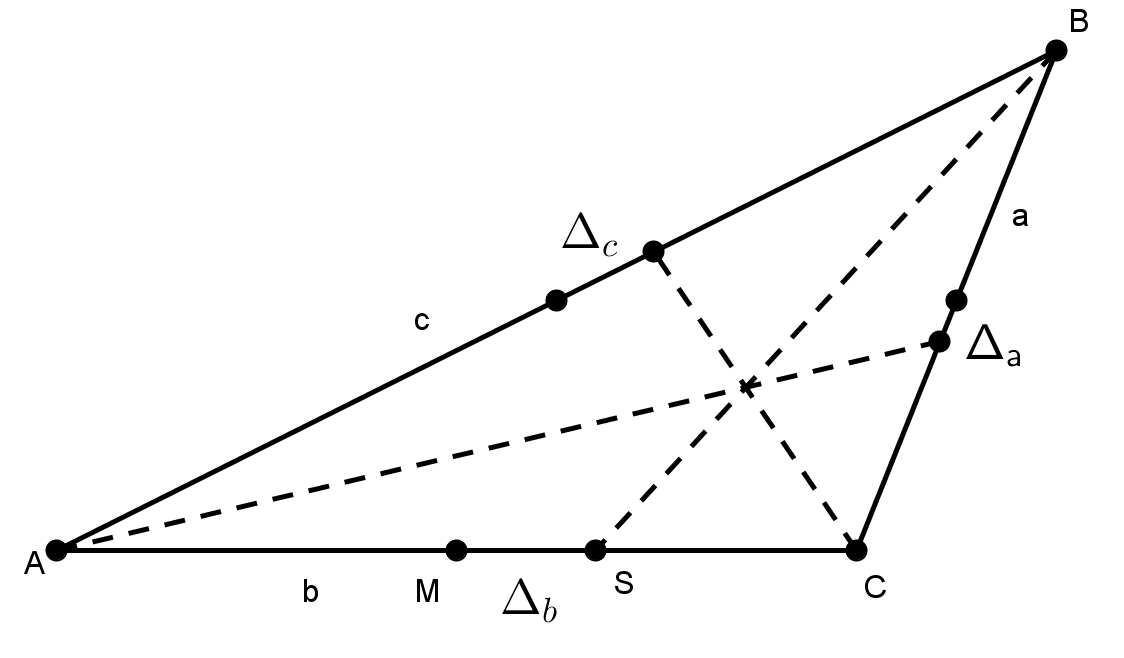
Рис. 34. Медианно-биссектральные отрезки

Получим, что

В первой из формул (4) числитель и знаменатель правой части почленно поделим на . В силу формулы (2) получим первую из формул (3). С двумя другими формулами можно поступить аналогично, с той разницей, что делить нужно на и соответственно.

Теорема 2. Индекс разносторонности угла треугольника выражается через длины образующих его сторон по формулам

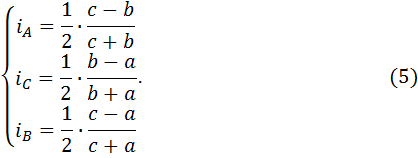
Доказательство. Если к первой из формул (3) применить основное свойство пропорции и выразить из полученного равенства индекс 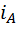, то получим первую из формул (5). Остальные формулы получаются аналогично.

Следствие. Индексы разносторонности углов треугольника принадлежат промежутку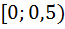

Доказательство непосредственно следует из формул (5).

Следующие три утверждения связывают индексы разносторонности и понятие подобия треугольников.

Предложение 3. Если треугольник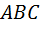и и 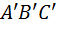подобны, то индексы разносторонности соответствующих углов равны.

Доказательство. Если коэффициент подобия равен 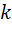, то по определению 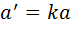, 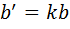и 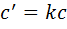. С помощью первой из формул (5) получаем, что

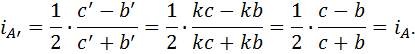
Остальные формулы получаются аналогично.

Предложение 4. Если два индекса разносторонности треугольника 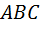соответственно равны двум индексам разносторонности треугольника 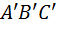, то такие треугольники подобны.

Доказательство. Пусть для определённости выполняются равенства 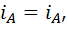и 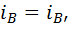. Из первого равенства следует, что . Домножим равенство на 2, применим основное свойство пропорции, раскроем скобки и приведём подобные члены. Получим, что 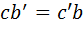, откуда 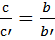. Аналогично из второго равенства получаем, что . И двух полученных пропорций вытекает подобие треугольников.

Доказательство для других пар равных индексов проводится аналогично.

Интересно, что предложение 4 по своей логической структуре похоже на признак подобия треугольников по двум углам.

Предложение 5. Индексы разносторонности определяют стороны треугольника с точностью до подобия.

Доказательство. В формулах (3) придадим стороне конкретное значение 1. Тогда из них следует, что 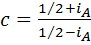и 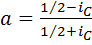. Окончательно получаем, что 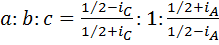. Аналогичные результаты получаются, если придавать конкретное значение не параметру , а другим параметрам.

Следующее утверждение связывает между собой все три индекса разносторонности.

Теорема 6. Индексы разносторонности треугольника удовлетворяют равенству

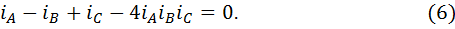
Доказательство. Первую из формул (3) умножим на вторую и поделим на третью. Получим равенство 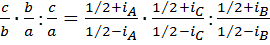, из которого следует, что

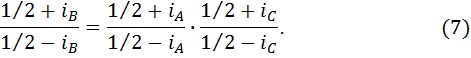
Применив к полученному равенству основное свойство пропорции, раскрыв скобки и приведя подобные члены, получим требуемое равенство (6).

В определённом смысле можно считать, что теорема 6 аналогична теореме о сумме углов треугольника. Действительно, зная два индекса разносторонности треугольника, можно по формуле (6) найти третий индекс, подобно тому, как по двум углам треугольника можно найти третий.

И формула (6), и в особенности формула (7) показывают, что индекс разносторонности среднего по величине угла 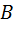играет особую роль по отношению к другим индексам. Это будет выявлено с помощью следующих двух утверждений о сравнении различных индексов.

Предложение 7. Если стороны треугольника удовлетворяют соотношению 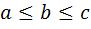, то для индексов разносторонности выполняются неравенства

Доказательство. Поделив индекс 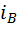на индекс 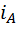, получим, что

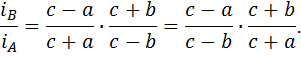
В силу условия теоремы каждая из дробей в правой части равенства больше единицы или равна ей, поэтому и 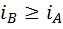. Второе неравенство доказывается аналогично.

Итак, чуть-чуть упрощая ситуацию, можно сказать, что средний по величине угол обладает наибольшим индексом разносторонности.

Следующий пример показывает, что соотношение типа «больше-меньше» между индексами разносторонности самого маленького и самого большого угла треугольника не является общим для всех треугольников.

Пример 1. Для каждого из треугольников 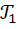, 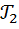и 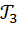, стороны которых заданы в таблице, вычислите индексы разносторонности углов и сравните их по величине.


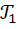
24	36	52
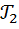
24	36	56
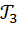
24	36	54

Решение. 1) Прямым вычислением по формулам (5) получаем, что индексы разносторонности треугольника 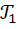принимают значения 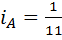, 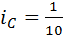и , так что выполняется неравенство .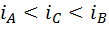

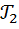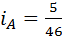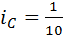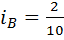2) Для треугольника значения индексов другие: , и , так что выполняется другое неравенство:

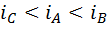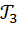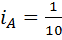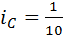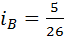3) Для треугольника значения индексов самые интересные: , и , поэтому одно из неравенств превращается в равенство: .

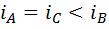Итак, мы видим, что разные по величине углы могут иметь одинаковые индексы разносторонности. Объяснение данного феномена даёт следующее утверждение.

Предложение 8. Пусть стороны треугольника удовлетворяют соотношению 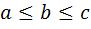. Тогда справедливы следующие утверждения. 1) тогда и только тогда, когда среднее геометрическое сторон и меньше средней стороны . 2) тогда и только тогда, когда среднее геометрическое сторон и больше средней стороны . 3) 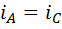тогда и только тогда, когда среднее геометрическое сторон и равно средней стороне .

Доказательство. Докажем первое утверждение. В силу формул (5) неравенство равносильно неравенству 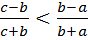. Пользуясь основным свойством пропорции, раскрывая скобки и приводя подобные члены, мы получим неравенство 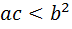, откуда и следует требуемое.

Два других утверждения теоремы доказываются аналогично.

Утверждение 3 предложения 8 можно трактовать как аналог теоремы Пифагора для треугольников с равными индексами разносторонност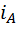и и 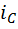. Действительно, оно означает, что . Другими словами, для треугольников с равными индексами разносторонности обращается в нуль квадратичная форма 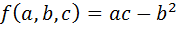, подобно тому, как для прямоугольных треугольников обращается в нуль другая квадратичная форма, а именно, .

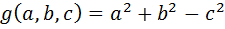Следующие два предложения выявляют геометрические следствия, вытекающие из достижения равенства в неравенствах (8).

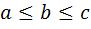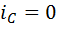Предложение 9. Пусть стороны треугольника удовлетворяют соотношению . 1) Если , то и 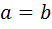, то есть треугольник является равнобедренным. 2) Если , то и 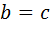, то есть треугольник является равнобедренным. 3) Если все три индекса разносторонности равны между собой, то треугольник является равносторонним.

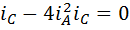Доказательство. 1) Если в формуле (6) положить , то она примет вид , откуда 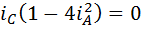. Второй сомножитель отличен от нуля в силу следствия из теоремы 2, поэтому 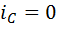. По второй из формул (5) получаем, что .

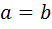Доказательство второго утверждения получается аналогично. Третье утверждение следует из первых двух.

Следующее утверждение является обратным к предложению 9.

Предложение 10. Если индекс разносторонности самого малого или самого большого угла равен нулю, то два других индекса разносторонности равны между собой и треугольник является равнобедренным. Если индекс разносторонности среднего по величине угла равен нулю, то два других индекса тоже равны нулю и треугольник является равносторонним.

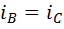Доказательство. Если , то по формуле (6) , а если 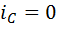, то по той же причине (6) . Если в формулах (8) положить 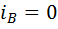, то два других индекса тоже обратятся в ноль.

Следующее предложение показывает возможность построения нового треугольника, в определённом смысле ассоциированного с исходным треугольником.

Теорема 11. Если длины трёх отрезков численно равны индексам разносторонности углов какого-либо разностороннего треугольника, то из них можно построить новый треугольник.

Доказательство. Если в левой части формулы (6) отбросить неотрицательный член 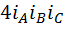, то она превратится в неравенство 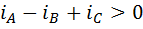, или 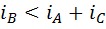. В силу предложения 7 получается, что самый длинный отрезок меньше суммы двух других, откуда вытекает возможность построения нового треугольника.

Следующий пример выявляет существенное отличие между индексами разносторонности и длинами mb -отрезков: из mb -отрезков далеко не всегда можно построить новый треугольник.

Пример 2. Для каждого из треугольников 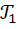и 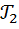, стороны которых заданы в таблице, вычислите длины mb-отрезков и сделайте выводы.


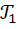
3	4	6
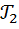
0,24	1	1,2

Решение. 1) Для треугольника 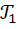прямым вычислением по формулам (2) и (5) получаем, что 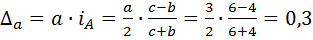. Аналогично получаем, что 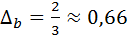, 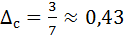. Очевидно, что самый длинный mb -отрезок 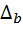короче суммы двух других mb -отрезков, поэтому из них можно построить треугольник.

2) Для треугольника 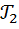ситуация оказывается иной. Действительно, 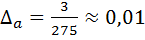, , 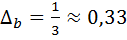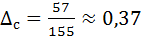. Очевидно, что самый длинный mb -отрезок 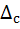длиннее суммы двух других mb -отрезков, поэтому из них невозможно построить треугольник.

Дата добавления: 2019-09-13; просмотров: 352; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 14 15 16 17 181920 21 22 23 Следующая ⇒

Мы поможем в написании ваших работ!