Числовая последовательность. Определение. Определение и геометрический смысл предела числовой последовательности.
ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ – функция вида y = f(x), x - N, где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, yn,…. Значения y1, y2, y3,… называют соответственно первым, вторым, третьим, … членами последовательности.
Число a называется пределом последовательности  , если для любого положительного числа
, если для любого положительного числа  можно указать такой номер , что при всех
можно указать такой номер , что при всех  выполняется неравенство
выполняется неравенство 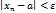 .
.
Если а есть предел последовательности 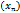 , то пишут
, то пишут  , или
, или  (
(  - три первые буквы латинского слова limes - «предел»).
- три первые буквы латинского слова limes - «предел»).
Это определение станет понятнее, если ему придать геометрический смысл. Заключим число а в интервал  . Число а есть предел последовательности
. Число а есть предел последовательности  , если независимо от малости интервала
, если независимо от малости интервала  все члены последовательности с номерами, большими некоторого
все члены последовательности с номерами, большими некоторого 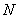 , будут лежать в этом интервале. Иными словами, вне любого интервала
, будут лежать в этом интервале. Иными словами, вне любого интервала  может находиться лишь конечное число членов последовательности.
может находиться лишь конечное число членов последовательности.
Основные теоремы о пределах.
Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
 Þ
Þ 
 .
.
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f ( x ) в окрестности некоторой точки не превосходят соответствующих значений функции g ( x ), то предел функции f ( x ) в этой точке не превосходит предела функции g ( x ).
 Þ
Þ 
 .
.
Теорема 3. Предел постоянной равен самой постоянной.
 .
.
Теорема 4. Функция не может иметь двух различных пределов в
одной точке.
Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при 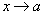 , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при 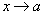 , причем предел алгебраической суммы равен алгебраической сумме пределов.
, причем предел алгебраической суммы равен алгебраической сумме пределов.
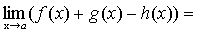

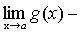
 .
.
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при 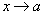 , то и произведение имеет предел при
, то и произведение имеет предел при 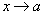 , причем предел произведения равен произведению пределов.
, причем предел произведения равен произведению пределов.
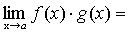
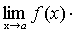
 .
.
Следствие. Постоянный множитель можно выносить за знак предела.


 .
.
Теорема 7. Если функции f ( x ) и g ( x ) имеют предел при 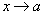 ,
,
причем  , то и их частное имеет предел при
, то и их частное имеет предел при 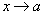 , причем предел частного равен частному пределов.
, причем предел частного равен частному пределов.
 ,
,  .
.
Бесконечно малая величина. Определение. Свойства бесконечно малых.
Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.
Последовательность 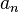 называется бесконечно малой, если
называется бесконечно малой, если 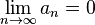 . Например, последовательность чисел
. Например, последовательность чисел  — бесконечно малая.
— бесконечно малая.
Функция называется бесконечно малой в окрестности точки 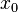 , если
, если  .
.
Функция называется бесконечно малой на бесконечности, если  либо
либо  .
.
Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то
, то 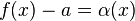 ,
, 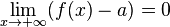 .
.
Подчеркнём, что бесконечно малую величину следует понимать как переменную величину (функцию), которая лишь в процессе своего изменения [при стремлении 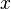 к
к 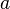 (из
(из  )] делается меньше произвольного числа (
)] делается меньше произвольного числа (  ). Поэтому, например, утверждение типа «одна миллионная есть бесконечно малая величина» неверно: о числе [абсолютном значении] не имеет смысла говорить, что оно бесконечно малое.
). Поэтому, например, утверждение типа «одна миллионная есть бесконечно малая величина» неверно: о числе [абсолютном значении] не имеет смысла говорить, что оно бесконечно малое.
Свойства:
· Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
· Произведение бесконечно малых — бесконечно малая.
· Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
· Если 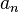 — бесконечно малая последовательность, сохраняющая знак, то
— бесконечно малая последовательность, сохраняющая знак, то  — бесконечно большая последовательность.
— бесконечно большая последовательность.
Дата добавления: 2019-09-13; просмотров: 424; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
