Примеры преобразования линейного дифференциального уравнения второго порядка к каноническому виду
Класификация линейных уравнений в частных производных второго порядка
Общий вид линейного уравнения второго порядка в частных производных
Уравнения математической физики, как правило, являются уравнениями второго порядка. Это связано с градиентной гипотезой замыкания уравнений баланса. Например, поток энтальпии пропорционален градиенту энтальпии – это гипотеза Фурье, поток концентрации пропорционален градиенту концентрации – это гипотеза Фика. Поток импульса в жидкости, связанный с трением, пропорционален градиенту скорости, гипотеза Стокса.
Общий вид линейного уравнения в частных производных второго порядка имеет вид
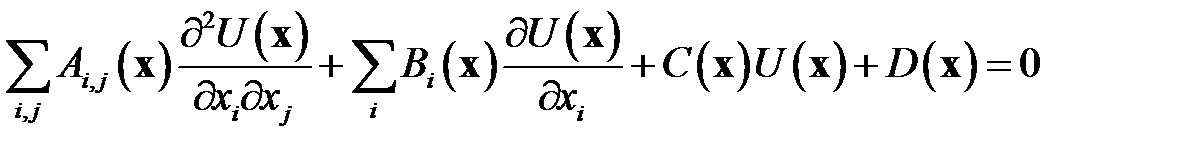
Матрица коэффициентов при старшей производной симметрична 
. Сделаем замену переменных
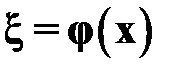
Вычисление производных в уравнении проводим следующим образом
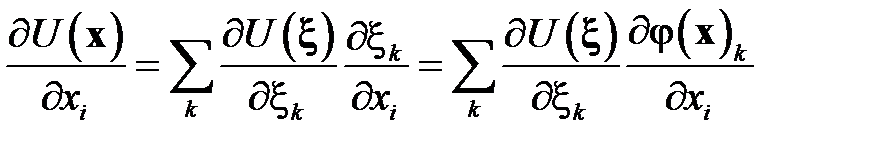
В результате подстановки этих выражений в уравнение , получаем
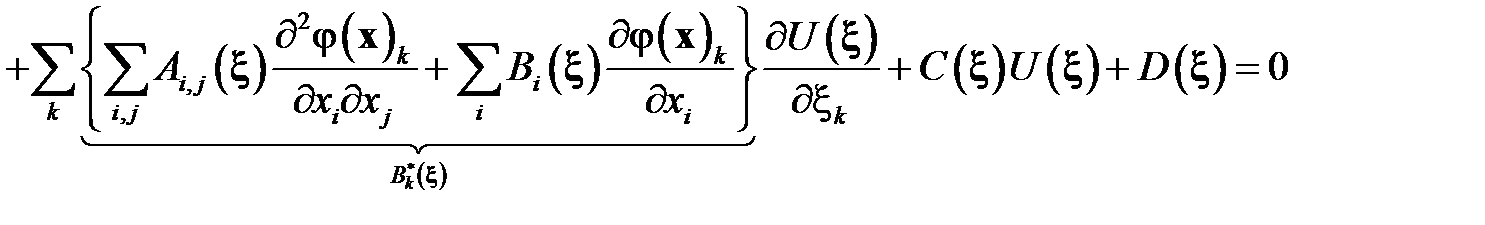
В компактном виде записываем
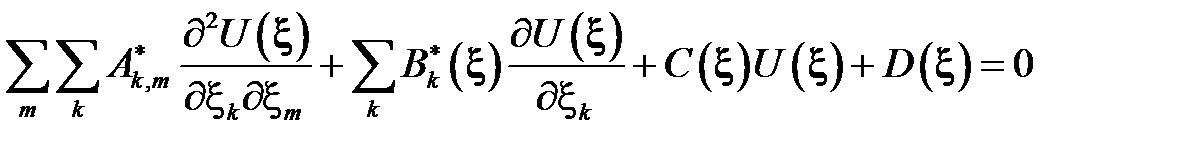
Здесь модифицированная матрица при старших производных и модифицированный вектор при производных первого порядка имеют вид
|
|
|
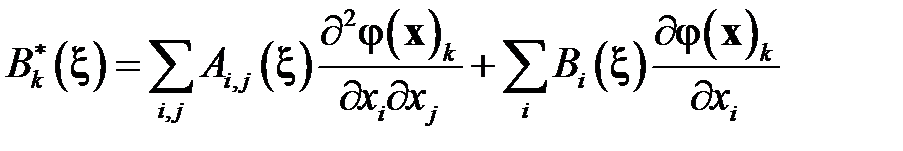
Приведение уравнения к каноническому виду
Из сравнения уравнений и видно, что порядок дифференциального уравнения в частных производных путем преобразования переменных изменить нельзя.
Из формулы видно, что преобразование переменных порождает матрицу преобразования, коэффициенты которой зависят от точки 
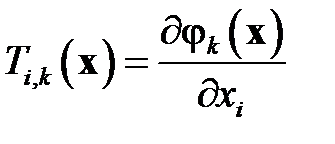
С учетом матрицы преобразования коэффициент при второй производной равен
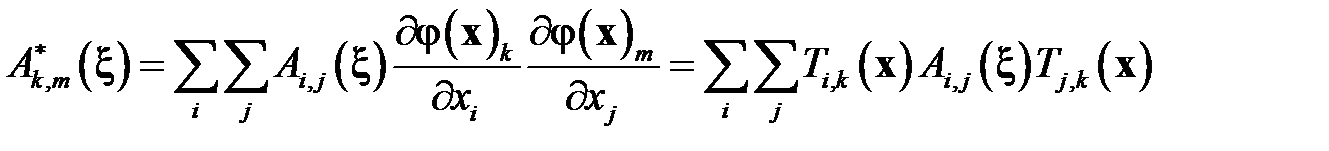
Матрица коэффициентов симметрична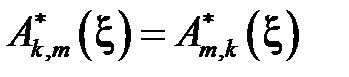 
. Из курса линейной алгебры известно, что симметричную матрицу можно привести к диагональному виду и что собственные значения этой матрицы вещественные числа.
Задача на собственные значения ставится следующим образом. Собственные вектора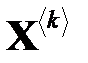 
и собственные значения 
матрицы 
находятся из решения следующей задачи
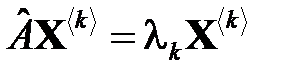
Собственные значения не зависят от преобразования системы координат . Для симметричной матрицы собственные значения – вещественны. Матрица преобразования стоится следующим образом
|
|
|
Выражение для модифицированной матрицы 
записывается в следующем виде
,
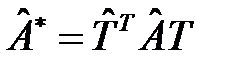где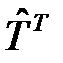 
– обозначает транспонированную матрицу к матрице 
.
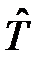Собственные значения матрицы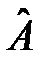 
не зависят от преобразования переменных и являются инвариантной характеристикой свойств дифференциального уравнения .
Классификация линейных дифференциальных уравнений второго порядка
В результате преобразования переменных с матрицей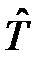 
уравнение приводится к каноническому виду
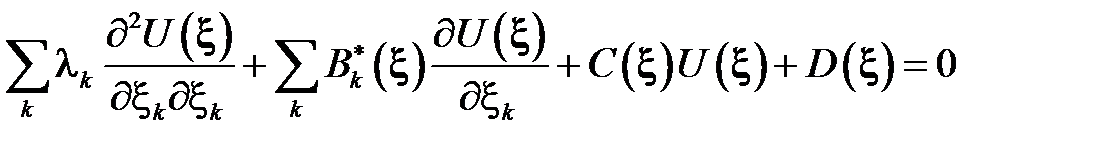
В зависимости от знаков собственных значений модифицированного уравнения различают три типа линейных дифференциальных уравнений в частных производных.
Собственные значения симметричной матрицы, стоящей перед вторыми производными могут быть следующих типов.
· Все собственные значения матрицы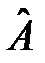 
имеют одинаковые знаки – это уравнение эллиптического типа.
|
|
|
· Собственные значения матрицы 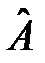имеют разные знаки – это уравнение гиперболического типа.
· Хотя бы одно собственно значение равно нулю – это уравнение параболического типа.
Тип уравнения может зависеть от координаты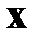 
.
Примеры преобразования линейного дифференциального уравнения второго порядка к каноническому виду
Дата добавления: 2019-09-13; просмотров: 124; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!