Теоретические методы определения параметров модели
Наиболее важными характеристиками вязкоупругого материала, определяющими его поведение под действием динамических нагрузок, являются частотные и амплитудные зависимости действительной 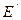 и мнимой
и мнимой 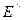 частей комплексного модуля
частей комплексного модуля
 . (1.16)
. (1.16)
Теперь рассмотрим зависимость комплексного модуля вязкоупругого тела от частоты, таким образом, как это было сделано для временных зависимостей ползучести и релаксации напряжения.
На рис. 1.3 показано изменение 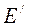 ,
,  и
и 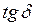 где
где  - угол фаз с частотой для эластомера, не проявляющего текучести. При низких частотах эластомер находится в высокоэластическом состоянии и имеет низкий модуль
- угол фаз с частотой для эластомера, не проявляющего текучести. При низких частотах эластомер находится в высокоэластическом состоянии и имеет низкий модуль  , не зависящий от частоты. При высоких частотах эластомер становится стеклообразным с модулем порядка 103 МПа, который также не зависит от частоты. При промежуточных частотах эластомер ведет себя как вязкоупругое тело и его модуль
, не зависящий от частоты. При высоких частотах эластомер становится стеклообразным с модулем порядка 103 МПа, который также не зависит от частоты. При промежуточных частотах эластомер ведет себя как вязкоупругое тело и его модуль 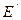 увеличивается с ростом частоты.
увеличивается с ростом частоты.
При низких и высоких частотах полимер имеет  , причем напряжения и деформация точно совпадают по фазе для высокоэластического (каучукоподобного) и стеклообразного состояний. При промежуточных частотах, когда эластомер является вязкоупругим,
, причем напряжения и деформация точно совпадают по фазе для высокоэластического (каучукоподобного) и стеклообразного состояний. При промежуточных частотах, когда эластомер является вязкоупругим, 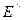 возрастает до максимальной величины, это наблюдается при частотах, близких к тем, при которых действительная часть модуля изменяется с частотой наиболее быстро. Область вязкоупругости характеризуется также максимумом
возрастает до максимальной величины, это наблюдается при частотах, близких к тем, при которых действительная часть модуля изменяется с частотой наиболее быстро. Область вязкоупругости характеризуется также максимумом 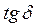 . Он проявляется при более низкой частоте, чем максимум
. Он проявляется при более низкой частоте, чем максимум  , так как
, так как  и
и  в этой области также быстро изменяется с частотой.
в этой области также быстро изменяется с частотой.
|
|
|

Рис.1.3. Частотная зависимость комплексного модуля от круговой частоты:
I – высокоэластичное состояние (каучукоподобное);
II – вязкоупругое состояние; III – стеклообразное состояние

Рис.1.4. Изменение напряжения и деформации в зависимости от угла ωt
при динамической нагрузке вязкоупругого материала

Рис.1.5. Кривая деформация – напряжение линейного вязкоупругого материала
Для линейного вязкоупругого тела при достижении установившегося режима напряжение и деформация изменяются по синусоидальному закону, но деформация отстает по фазе от напряжения (рис. 1.17). Таким образом, можно записать
 , (1.17)
, (1.17)
 , (1.18)
, (1.18)
где  – круговая частота;
– круговая частота;  – угол сдвига фаз.
– угол сдвига фаз.
Если уравнения (1.17) и (1.18) для деформации и напряжения записать в комплексной форме
 , (1.19)
, (1.19)
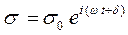 , (1.20)
, (1.20)
|
|
|
то комплексный модуль равен
 , (1.21)
, (1.21)
где модуль упругости системы 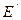 (действительная часть комплексного модуля, совпадающая по фазе с деформацией) характеризует упругую энергию, запасаемую в образце при деформировании, а модуль потерь
(действительная часть комплексного модуля, совпадающая по фазе с деформацией) характеризует упругую энергию, запасаемую в образце при деформировании, а модуль потерь  (мнимая часть
(мнимая часть
комплексного модуля) характеризует величину рассеянной энергии. Далее очевидно, что тангенс угла механических потерь
 . (1.22)
. (1.22)
Эти уравнения справедливы для любого линейного вязкоупругого тела безотносительно к выбранной реологической модели [5,6,28].
Для математического описания частотной зависимости динамических свойств необходимы следующие преобразования.
Отношение напряжение - деформация модели Максвелла показанной на рис. 1.2 а, имеет вид [27]

 . (1.23)
. (1.23)
Определяя время релаксации как  , можно записать
, можно записать
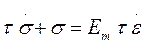 . (1.24)
. (1.24)
Дата добавления: 2019-09-13; просмотров: 348; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
