Инвариантность (неизменность формы записи) дифференциала первого порядка.
Пусть z = f ( x ; y ) 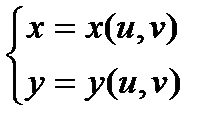 .
.
Все функции предполагаются дифференцируемыми. Рассмотрим дифференциал от такой функции.
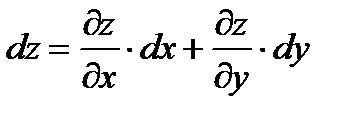 =
= 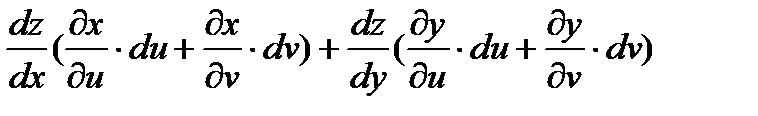 .
.
Раскроем скобки, перегруппируем слагаемые и вынесем общие множители du и dv.
Имеем: 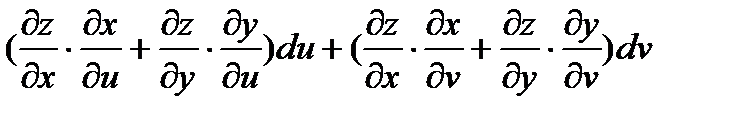 =
= 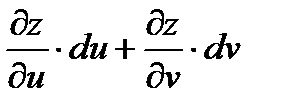
Вывод: Форма дифференциала первого порядка не изменяется если функция является сложной. Дифференциалы высших порядков этим свойством не обладают.
Производная неявной функции.
Определение: Функция 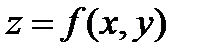 называется неявной, если она задается уравнением
называется неявной, если она задается уравнением 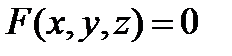 неразрешимым относительно z.
неразрешимым относительно z.
Начнем рассмотрение с неявной функции одного переменного : F(x,y)=0.
Теорема:
Пусть непрерывная функция y(x) задается неявно уравнением вида F(x,y)=0 и  ,
, 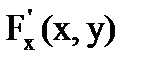 ,
, 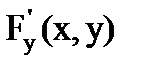 - непрерывные функции в области D, содержащей точку (x,y), удовлетворяющую уравнению F(x,y)=0. Кроме того, в этой точке
- непрерывные функции в области D, содержащей точку (x,y), удовлетворяющую уравнению F(x,y)=0. Кроме того, в этой точке 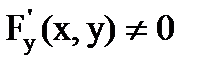 , тогда функция y(x) имеет производную
, тогда функция y(x) имеет производную  .
.
Доказательство:
Пусть некоторому значению x соответствует значение y, причем выполняется F(x,y)=0. Возьмем для независимой переменной x приращение 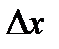 . Функция y, при этом, получит приращение
. Функция y, при этом, получит приращение 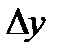 . То есть значению аргумента
. То есть значению аргумента 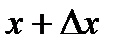 будет соответствовать значение функции
будет соответствовать значение функции 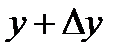 . А в силу уравнения F(x,y)=0 имеем:
. А в силу уравнения F(x,y)=0 имеем: 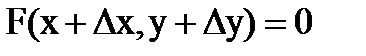 и, соответственно
и, соответственно 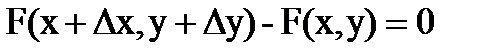 . Левую, часть, являющуюся полным приращением функции двух переменных можно представить в виде
. Левую, часть, являющуюся полным приращением функции двух переменных можно представить в виде 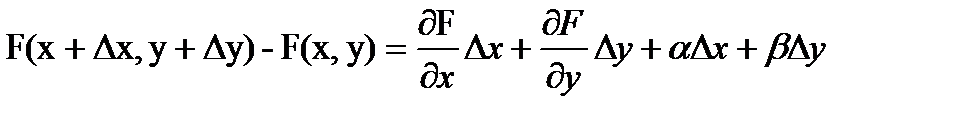 , где
, где 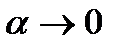 ,
, 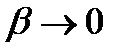 , при
, при 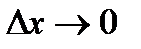 и
и 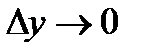 . Или иначе (поскольку правая часть равенства - ноль):
. Или иначе (поскольку правая часть равенства - ноль): 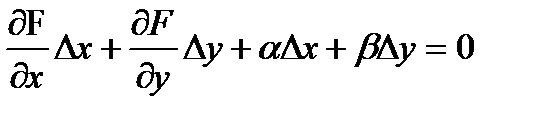 . Разделим последнее равенство на
. Разделим последнее равенство на 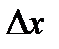 и вычислим
и вычислим 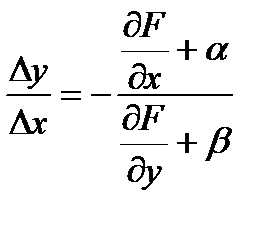 . Устремим
. Устремим 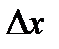 к нулю. Тогда учитывая, что
к нулю. Тогда учитывая, что 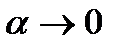 ,
, 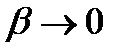 , при
, при 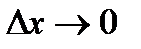 и
и 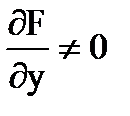 в пределе получим
в пределе получим 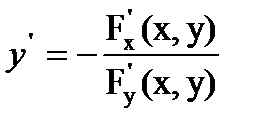 . Таким образом, доказана теорема существования производной от функции, заданной неявно.
. Таким образом, доказана теорема существования производной от функции, заданной неявно.
|
|
|
Пример:
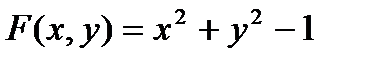 .
.
Решение:
Найдем производную.
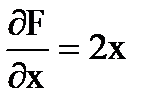 ,
, 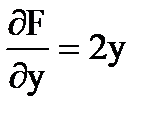 .
.
Следовательно, 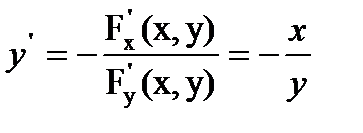 .
.
Рассмотрим теперь функцию вида 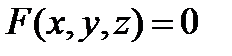 . Найдем частные производные функции неявной функции z. Для этого подставив в уравнение вместо z,
. Найдем частные производные функции неявной функции z. Для этого подставив в уравнение вместо z, 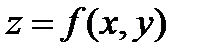 , получим тождество
, получим тождество 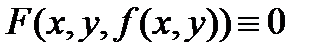 . Частные производные функции тождественно равной нулю также равны нулю.
. Частные производные функции тождественно равной нулю также равны нулю.
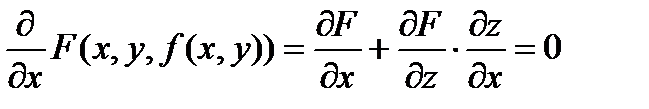
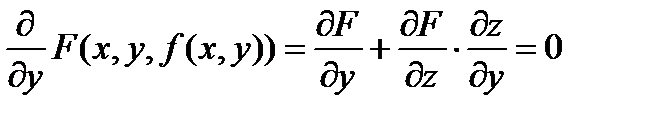
Откуда: 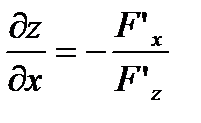 ,
,  .
.
Аналогично определяются производные неявно заданных функций произвольного числа переменных.
Пример :

Решение :
Так как
 Þ
Þ 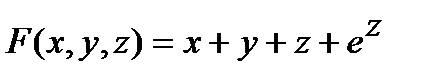
Найдем частные производные:
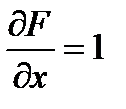 ;
; 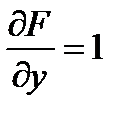 ;
; 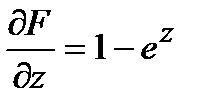 .
.
Следовательно:
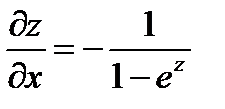 ;
;  .
.
Пример:
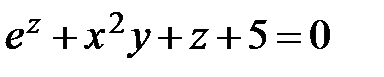
Решение:
Найдем частные производные:
 ;
; 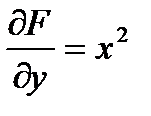 ;
; 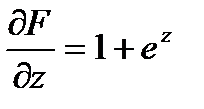 .
.
Следовательно:
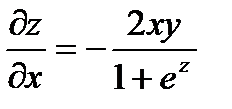 ;
; 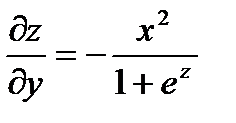 .
.
Касательная плоскость и нормаль к поверхности.
Определение: Плоскость, в которой распложены все касательные к линиям на поверхности, проходящим через точку касания M0, называется касательной плоскостью к поверхности в точке M0.
Определение: Нормалью к поверхности называется прямая перпендикулярная касательной плоскости и проходящая через точку касания.
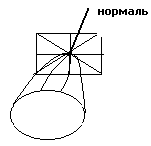 Так как нормаль перпендикулярна касательной плоскости, то в качестве направляющего вектора можно взять вектор нормали к касательной плоскости (координаты вектора нормали - это частные производные.)
Так как нормаль перпендикулярна касательной плоскости, то в качестве направляющего вектора можно взять вектор нормали к касательной плоскости (координаты вектора нормали - это частные производные.)
|
|
|
Тогда уравнение нормали имеет вид:
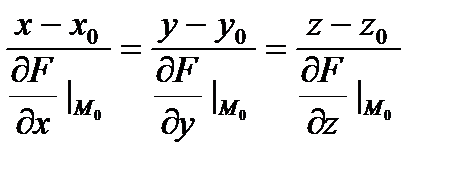 ;
;
То есть если уравнение поверхности задано в виде z=f(x,y), точка M0(x0,y0) и f(x0,y0) принадлежат поверхности, точка M0 – точка касания, тогда уравнение касательной плоскости имеет вид: 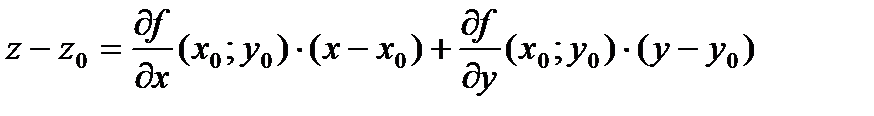 .
.
А в случае поверхности, заданной уравнением вида F(x,y,z)=0, уравнение касательной плоскости имеет вид: 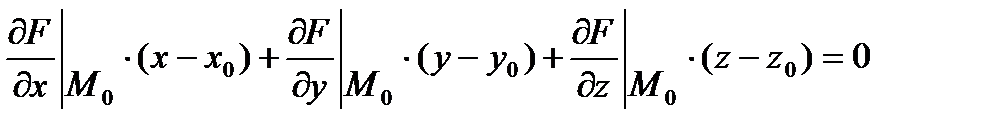 , где
, где
точка M0(x0,y0,z0) – точка касания.
Каноническое уравнение прямой в пространстве 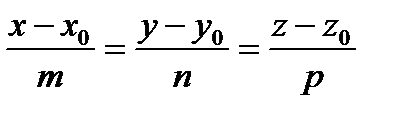
Пример: Написать уравнение касательной плоскости и нормали к поверхности 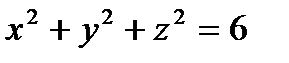 в точке M0(1,2,-1).
в точке M0(1,2,-1).
Решение:
Преобразуем: 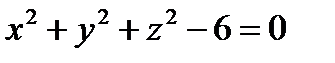 .
.
Найдем значения частных производных в заданной точке (это координаты вектора нормали к плоскости):
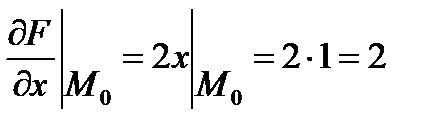 ;
; 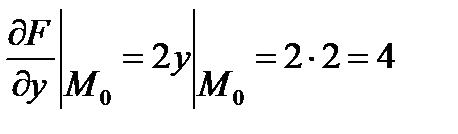 ;
; 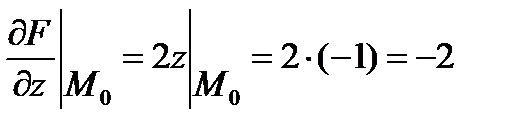 .
.
Уравнение плоскости имеет вид:
2(x-1)+4(y-2)-2(z+1)=0.
Или иначе (раскрыв скобки и приведя подобные):
2x+4y-2z-8=0.
Дата добавления: 2019-09-13; просмотров: 231; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
