Критерий Коши сходимости ряда
В приведенных примерах п. 1.1 нам удавалось не только установить сходимость или расходимость рассматриваемых рядов, но и найти их суммы (в случае сходимости ряда). Непосредственный анализ последовательности 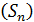 не всегда представляется возможным. Так как на практике частичные суммы ряда (в случае его сходимости) принимают за приближенное значение суммы ряда, то представляет интерес выяснение вопроса о сходимости или расходимости числового ряда без вычисления величины его суммы, а также оценка зависимости остатка ряда
не всегда представляется возможным. Так как на практике частичные суммы ряда (в случае его сходимости) принимают за приближенное значение суммы ряда, то представляет интерес выяснение вопроса о сходимости или расходимости числового ряда без вычисления величины его суммы, а также оценка зависимости остатка ряда  от номера n (скорость сходимости ряда). Наиболее общий критерий сходимости числового ряда вытекает из критерия Коши для сходимости последовательности.
от номера n (скорость сходимости ряда). Наиболее общий критерий сходимости числового ряда вытекает из критерия Коши для сходимости последовательности.
(Коши Огюстен Луи (1789-1857) – французский математик, член Парижской Академии наук.)
Теорема 1. Ряд  сходится тогда и только тогда, когда
сходится тогда и только тогда, когда
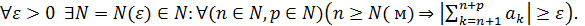
Если условие (2.1) не выполняется, т.е. если
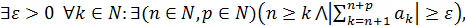 то ряд
то ряд  расходится.
расходится.
Определение. Ряд 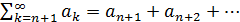 называют остатком ряда
называют остатком ряда  и обозначают
и обозначают 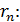

Из теоремы 1 легко получить следующее важное утверждение.
Теорема 2. Ряд 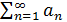 сходится или расходится одновременно с рядом
сходится или расходится одновременно с рядом 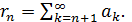 При этом
При этом 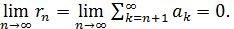
Следствие. Прибавление (отбрасывание, изменение) конечного числа членов не влияет на сходимость ряда (но может, конечно, изменить его сумму).
Так как для сходящегося ряда 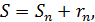 то при достаточно больших n можно считать, что
то при достаточно больших n можно считать, что 
Пример 15. Пользуясь критерием Коши, доказать сходимость ряда  .
.
|
|
|
Пусть 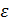 – произвольное положительное число. Так как
– произвольное положительное число. Так как
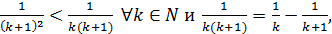 то
то 
 при произвольном
при произвольном 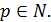 Отсюда следует, что при
Отсюда следует, что при 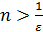
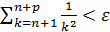 .
.
Таким образом, взяв 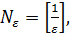 получим, что при
получим, что при  и произвольном p выполняется требуемое неравенство, и ряд сходится.
и произвольном p выполняется требуемое неравенство, и ряд сходится.
Пример 16. Покажем с помощью критерия Коши, что обобщенный гармонический ряд 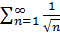 расходится.
расходится.
Для любого 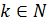 возьмем n = k и p = k. Тогда
возьмем n = k и p = k. Тогда
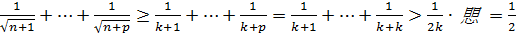
Итак, для 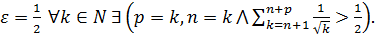 Следовательно, ряд
Следовательно, ряд 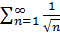 расходится.
расходится.
2. 2. Необходимое условие сходимости ряда
Из критерия Коши сходимости ряда вытекает
Теорема 3. Если ряд 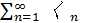 суммируем, то предел его общего члена равен нулю:
суммируем, то предел его общего члена равен нулю:
 (2.3)
(2.3)
Замечание. Как утверждается в теореме, для сходимости ряда необходимо, чтобы  Таким образом, если
Таким образом, если  то ряд
то ряд  заведомо расходится.
заведомо расходится.
Наоборот, если 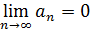 , то ряд не обязательно является сходящимся. Пример гармонического ряда показывает, что это условие не является достаточным: ряд
, то ряд не обязательно является сходящимся. Пример гармонического ряда показывает, что это условие не является достаточным: ряд  расходится, хотя при этом
расходится, хотя при этом
 .
.
Для сходимости ряда недостаточно, чтобы n-й член ряда стремился к нулю; нужно, чтобы он стремился к нулю достаточно быстро (обсуждение этого вопроса в п. 3. 2).
Пример 17. Рассмотрим ряд
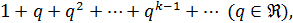 (2.4)
(2.4)
|
|
|
составленный из членов геометрической прогрессии: 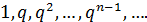 Его
Его
часто называют геометрическим рядом. Исследуем сходимость данного ряда.
Если 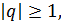 то
то  следовательно,
следовательно, 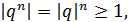 и в этом случае не выполнен необходимый признак сходимости. Итак, в случае
и в этом случае не выполнен необходимый признак сходимости. Итак, в случае 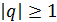 ряд (2. 4) расходится.
ряд (2. 4) расходится.
Пусть  . Тогда
. Тогда 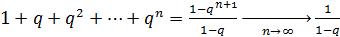 , поскольку
, поскольку 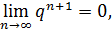 если
если  . Значит, ряд в этом случае сходится.
. Значит, ряд в этом случае сходится.
Наоборот, если ряд (2. 4) суммируем, то 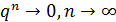 и, следовательно,
и, следовательно,  .
.
Таким образом, геометрический ряд суммируем тогда и только тогда, когда  , и в этом случае его сумма:
, и в этом случае его сумма:
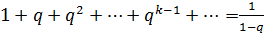 . (2.5)
. (2.5)
Пример 18. Ряд 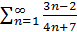 расходится, ибо
расходится, ибо
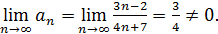
Пример 19. Ряд 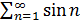 расходится, т.к. последовательность
расходится, т.к. последовательность 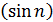 не является бесконечно малой. В самом деле, предположим противное:
не является бесконечно малой. В самом деле, предположим противное:  . Тогда
. Тогда 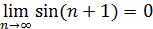 . Так как
. Так как
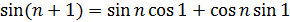 , то
, то 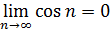 , что противоречит равенству
, что противоречит равенству  . Следовательно, рассматриваемый ряд расходится.
. Следовательно, рассматриваемый ряд расходится.
2. 3. Алгебраические операции и сходимость
Теорема 4. Пусть 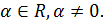 Ряды
Ряды  и
и 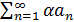 одновременно сходятся или расходятся. Если один из них сходится, то
одновременно сходятся или расходятся. Если один из них сходится, то 
Теорема 5. Два сходящихся ряда можно почленно складывать и вычитать, то есть, если ряды  и
и  сходятся, то ряд
сходятся, то ряд 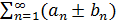 тоже сходится, причем
тоже сходится, причем
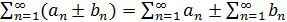 .
.
Следствие. Если два ряда  и
и  сходятся, то для любых
сходятся, то для любых 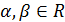 ряд
ряд  также сходится и
также сходится и
|
|
|
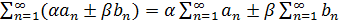 .
.
Пример 20. Найдем сумму ряда  Данный ряд можно представить как сумму двух рядов:
Данный ряд можно представить как сумму двух рядов: 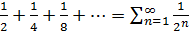 и
и
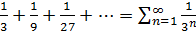 . Каждый из них является геометрическим рядом со знаменателем
. Каждый из них является геометрическим рядом со знаменателем  , а потому сходится. По формуле (2. 5) суммы первого и второго рядов соответственно равны:
, а потому сходится. По формуле (2. 5) суммы первого и второго рядов соответственно равны:
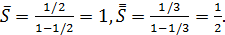
Тогда по теореме 5 
Теорема 6. Если ряд  сходится, а ряд
сходится, а ряд  расходится, то ряд
расходится, то ряд 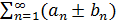 расходится.
расходится.
Пример 21. Рассмотрим ряд 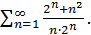
Так как  и ряд
и ряд 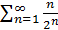 сходится (см. п. 1. 1, пример 14), а гармонический ряд
сходится (см. п. 1. 1, пример 14), а гармонический ряд  расходится, то ряд
расходится, то ряд 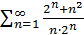 расходится.
расходится.
Теорема 7. Если оба ряда  и
и  расходятся, то ряд
расходятся, то ряд 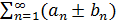 может как сходиться, так и расходиться.
может как сходиться, так и расходиться.
Пример 22. Рассмотрим ряд 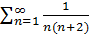 .
.
Так как 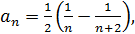 то
то 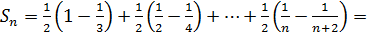
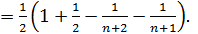 Следовательно,
Следовательно, 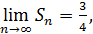 т.е. ряд
т.е. ряд 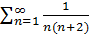 сходится, и его сумма равна
сходится, и его сумма равна 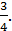 В то же время каждый из рядов
В то же время каждый из рядов  и
и  является расходящимся. Расходимость второго ряда очевидна: он получается из гармонического отбрасыванием двух его первых членов.
является расходящимся. Расходимость второго ряда очевидна: он получается из гармонического отбрасыванием двух его первых членов.
Дата добавления: 2019-09-02; просмотров: 287; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
