Универсальная тригонометрическая подстановка.
Рассмотрим некоторые случаи нахождения интеграла от тригонометрических функций. Функцию с переменными 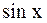 и
и  над которым выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать
над которым выполняются рациональные действия (сложения, вычитание, умножение и деление) принято обозначать 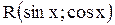 , где R — знак рациональной функции.
, где R — знак рациональной функции.
Вычисление неопределенных интегралов типа 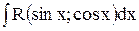 , сводится к вычислению интегралов от рациональной функции подстановкой
, сводится к вычислению интегралов от рациональной функции подстановкой  , которая называется универсальной. Тогда получаем,
, которая называется универсальной. Тогда получаем,  ,
, 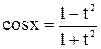 ,
, 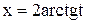 ,
,  .
.
На практике применяют и другие, более простые подстановки, в зависимости от свойств и вида подынтегральной функции. В частности, удобны следующие правила:
1) если функция 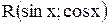 нечетна относительно
нечетна относительно 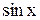 , т. е,
, т. е, 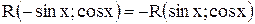 , то подстановка
, то подстановка  рационализирует интеграл;
рационализирует интеграл;
2) если функция 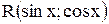 нечетна относительно
нечетна относительно  , т. е.
, т. е. 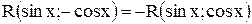 , то делается подстановка
, то делается подстановка 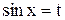 ;
;
3) если функция  четна относительно
четна относительно 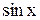 u
u 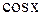
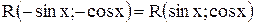 , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой 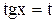 . Такая же подстановка применяется, если интеграл имеет вид
. Такая же подстановка применяется, если интеграл имеет вид 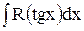 .
.
Пример 6.
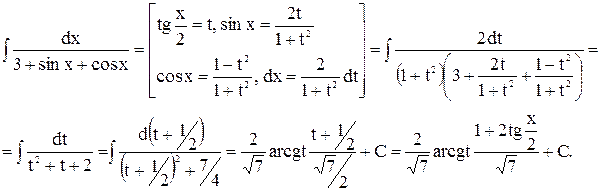
6. Интегралы типа 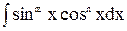 .
.
Для нахождения таких интегралов используются следующие приемы:
1) подстановка  , если n - целое положительное нечетное число;
, если n - целое положительное нечетное число;
2) подстановка  , если m - целое положительное нечетное число;
, если m - целое положительное нечетное число;
3) формулы понижения степени: 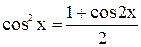 ,
,  ,
, 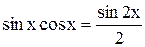 , если m и n - целые неотрицательные четные числа;
, если m и n - целые неотрицательные четные числа;
4) подстановка 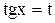 , если
, если 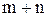 - есть четное отрицательное целое число.
- есть четное отрицательное целое число.
Интегралы типа  ,
, 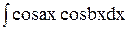 ,
,  вычисляются с помощью известных формул тригонометрии:
вычисляются с помощью известных формул тригонометрии:
|
|
|

Пример 7.
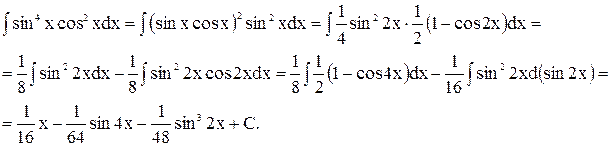

Интегрирование иррациональных функций.
Рассмотрим некоторые типы интегралов, содержащих иррациональные функции.
Интегралы типа  ,
, 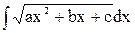 ,
, 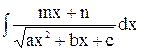 называются неопределёнными интегралами от квадратичных иррациональностей. Их можно найти следующим образом: под интегралом выделить полный квадрат:
называются неопределёнными интегралами от квадратичных иррациональностей. Их можно найти следующим образом: под интегралом выделить полный квадрат:
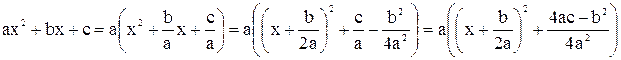
и сделать подстановку 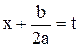 . При этом первые два интеграла приводятся к табличным, а третий к сумме двух табличных.
. При этом первые два интеграла приводятся к табличным, а третий к сумме двух табличных.
Дробно – линейная подстановка.
Интегралы типа 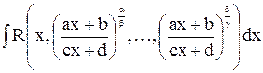 , где
, где  ,
,  ,
,  и
и 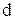 - действительные числа,
- действительные числа, 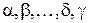 - натуральные числа, сводятся к интегралам от рациональной функции путём подстановки
- натуральные числа, сводятся к интегралам от рациональной функции путём подстановки 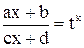 , где
, где  - наименьшее общее кратное знаменателей дробей
- наименьшее общее кратное знаменателей дробей 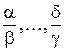 .
.
Пример 8.
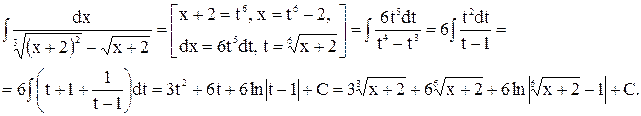
Тригонометрическая подстановка.
Интегралы типа 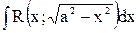 ,
,  ,
, 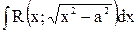 приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью следующих тригонометрических подстановок:
приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью следующих тригонометрических подстановок:  для первого интеграла;
для первого интеграла; 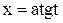 для второго интеграла;
для второго интеграла; 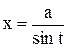 для третьего интеграла.
для третьего интеграла.
Пример 9.
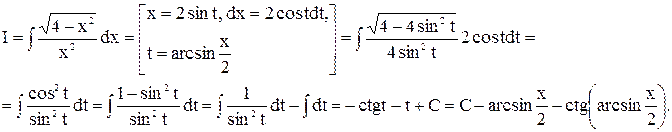
Интегрирование дифференциального бинома.
Интегралы типа 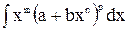 (называемые интегралами от дифференциального бинома), где
(называемые интегралами от дифференциального бинома), где 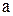 ,
, 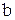 - действительные числа;
- действительные числа; 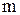 ,
, 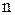 ,
, 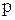 - рациональные числа, берутся, лишь в случае, когда хотя бы одно из чисел
- рациональные числа, берутся, лишь в случае, когда хотя бы одно из чисел 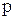 ,
, 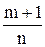 или
или 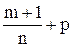 - является целым.
- является целым.
|
|
|
Рационализация интеграла в этих случаях осуществляется следующими подстановками:
1) если 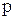 - целое число, то подстановка
- целое число, то подстановка  , где
, где 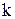 наименьшее общее кратное знаменателей дробей
наименьшее общее кратное знаменателей дробей 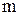 и
и 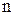 ;
;
2) если 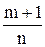 -целое число, то подстановка
-целое число, то подстановка 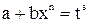 , где
, где 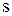 - знаменатель дроби
- знаменатель дроби 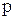 ;
;
3) если 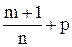 - целое число, то подстановка
- целое число, то подстановка 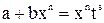 где
где 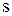 - знаменатель дроби
- знаменатель дроби 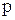 ;
;
Во всех остальных случаях интегралы типа  не выражаются через известные элементарные функции, т. е. «не берутся».
не выражаются через известные элементарные функции, т. е. «не берутся».
Неберущиеся» интегралы.
Изученные методы интегрирования позволяют во многих случаях вычислить неопределенный интеграл, т. е. найти первообразную функцию для подынтегральной функции.
Как известно, всякая непрерывная функция имеет первообразную. В том случае, когда первообразная некоторой элементарной функции 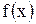 является также элементарной функцией, говорят, что
является также элементарной функцией, говорят, что  «берется», т. е. интеграл выражается через элементарные функции (или интеграл вычисляется). Если же интеграл не выражается через элементарные функции, то говорят, что интеграл «не берется» или «его найти нельзя».
«берется», т. е. интеграл выражается через элементарные функции (или интеграл вычисляется). Если же интеграл не выражается через элементарные функции, то говорят, что интеграл «не берется» или «его найти нельзя».
Так, например, нельзя взять интеграл 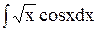 , так как не существует элементарной функции, производная от которой была бы раина
, так как не существует элементарной функции, производная от которой была бы раина  . Приведем еще примеры «неберущихся» интегралов:
. Приведем еще примеры «неберущихся» интегралов:
|
|
|
1) 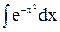 — интеграл Пуассона;
— интеграл Пуассона;
2) 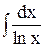 интегральный логарифм;
интегральный логарифм;
3) 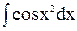 ,
,  - интегралы Френеля;
- интегралы Френеля;
4) 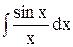 ,
, 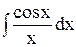 - интегральные синус и косинус.
- интегральные синус и косинус.
Пример 10.
1) 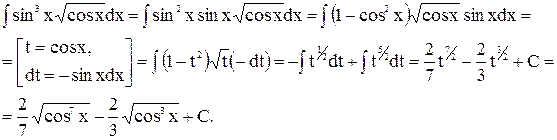
2) 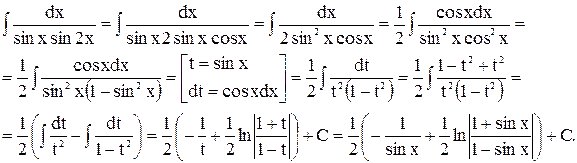
Дата добавления: 2019-09-02; просмотров: 249; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
