ОБЩИЕ СВЕДЕНИЯ О ЗАДАЧЕ КОМПОНОВКИ
В настоящее время в радиоэлектронике принят функциональноузловой метод проектирования . Он предусматривает расчленение радиоэлектронных средств (РЭС) на отдельные конструктивно законченные единицы (модули) различных уровней (рангов). Это могут быть отдельные платы – типовые элементы замены (ТЭЗы), функциональные узлы, субблоки, блоки, панели, пульты, стойки. В связи с этим при разработке конструкций РЭС проек-тировщик неизбежно сталкивается с задачей распределения элементов схемы низшего уровня по коммутационным пространствам модулей данного уровня иерархии. При ее решении основным критерием оптимальности компоновки модулей является минимизация числа межмодульных связей, что необходимо для повышения надежности схем (за счет уменьшения числа разъемных соединений), уменьшения влияния наводок и времени задержки сигнала в цепях (вследствие минимизации суммарной длины соединений), упрощения кон-струкции и повышения технологичности разрабатываемого устройства.
Математическая формулировка задачи
Для алгоритмизации и формального решения задачи компоновки РЭС производится переход от электрической схемы соединений РЭС к мультиграфу. При этом каждому конструктивному элементу (модулю) ставят в соответствии вершину мультиграфа, а электрическим связям схемы – его ребра. В этом случае задача компоновки формулируется следующим образом [2 – 5].
|
|
|
Дан мультиграф 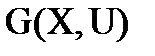 . Требуется разбить («разрезать») его на отдельные куски
. Требуется разбить («разрезать») его на отдельные куски 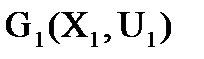 ,
, 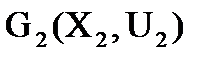 ,…,
,…,  так, чтобы число ребер, соединяющих эти куски, было минимальным. Это значит надо минимизировать функцию:
так, чтобы число ребер, соединяющих эти куски, было минимальным. Это значит надо минимизировать функцию:
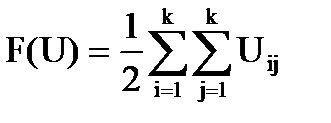 , где
, где 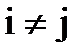 (2.1)
(2.1)
При разбиении графа на куски 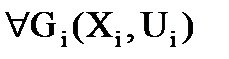 ,
, 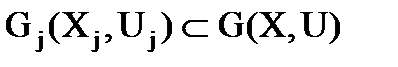 задаются следующие ограничения:
задаются следующие ограничения:
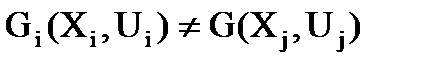 , (2.2)
, (2.2)
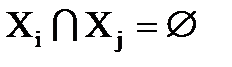 , (2.3)
, (2.3)
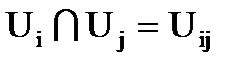 , (2.4)
, (2.4)
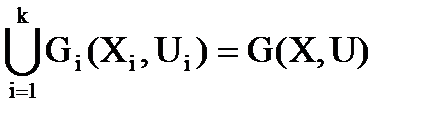 ;
; 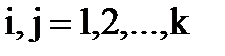 , (2.5)
, (2.5)
где Uij – множество ребер, соединяющих куски 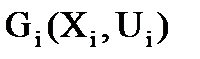 и
и 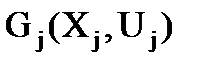 .
.
Другими словами, совокупность кусков разбиения графа  является разбиением графа G, если любой кусок из этой совокупности не пустой
является разбиением графа G, если любой кусок из этой совокупности не пустой
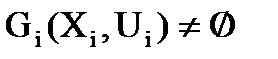 , (2.6)
, (2.6)
и для любых двух кусков 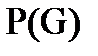 пересечение множества вершин – пустое множество (2.3), а пересечение множества ребер (2.4) может быть не пустым. Кроме этого объединение всех кусков (2.5) должно в точности равняться графу G.
пересечение множества вершин – пустое множество (2.3), а пересечение множества ребер (2.4) может быть не пустым. Кроме этого объединение всех кусков (2.5) должно в точности равняться графу G.
В выражении (2.4) множество 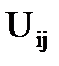 определяет подмножество ребер
определяет подмножество ребер 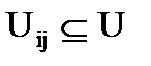 , попадающих в разрез (сечение) между кусками
, попадающих в разрез (сечение) между кусками 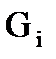 и
и 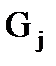 графа G.
графа G.
Конструктивными ограничениями в задачах компоновки являются:
а) максимально допустимое количество вершин t в куске
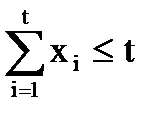 ; (2.7)
; (2.7)
|
|
|
б) число кусков разрезания графа
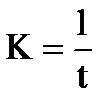 , (2.8)
, (2.8)
где l – количество вершин в исходном графе;
в) максимальное число внешних связей каждого отдельного куска 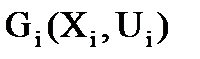 графа
графа 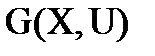
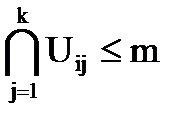 . (2.9)
. (2.9)
Физический смысл ограничений (2.2) – (2.9) следующий.
Условия (2.2) – (2.4) означают, что не может быть двух узлов, содержащих один и тот же элемент, вместе с тем электрические цепи, соединяющие отдельные узлы существуют.
Условие (2.5) – суммарное число элементов, входящих в отдельные узлы, равно количеству элементов, входящих в электрическую схему всего устройства.
Условие (2.6) – не может быть узла, в котором не содержится ни одного элемента.
Условие (2.7) – соответствует числу конструктивных элементов, которые необходимо разместить в коммутационном пространстве, (2.8) – требуемое число узлов, в которые требуется скомпоновать конструктивные элементы устройства, (2.9) – определяет количество контактов используемого разъема.
Для оценки качества компоновки схемы в узлы, что соответствует оценке качества разбиения на куски, введем понятие коэффициента разбиения 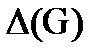 . Для этого допустим, что граф G разбит на k кусков:
. Для этого допустим, что граф G разбит на k кусков: 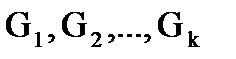 . Тогда множество ребер U графа G можно представить в виде
. Тогда множество ребер U графа G можно представить в виде
|
|
|
 . (2.10)
. (2.10)
Каждое подмножество 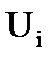 запишем следующим образом:
запишем следующим образом:
 ,
,
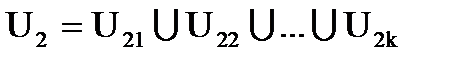 (2.11)
(2.11)
……………………………
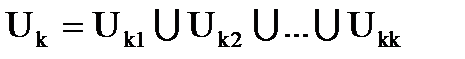 ,
,
где 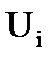 – подмножество всех ребер, инцидентных вершинам
– подмножество всех ребер, инцидентных вершинам 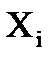 куска
куска 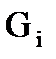 ;
; 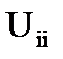 – подмножество ребер, соединяющих подмножество вершин
– подмножество ребер, соединяющих подмножество вершин 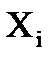 куска
куска 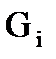 между собой;
между собой; 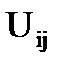 (или
(или  ) – подмножество ребер, соединяющих куски
) – подмножество ребер, соединяющих куски 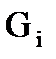 и
и 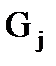 .
.
Тогда отношение суммарного числа внутренних ребер (ребер подмножеств 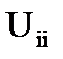 ) к суммарному числу соединительных ребер (ребер подмножеств
) к суммарному числу соединительных ребер (ребер подмножеств 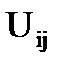 ) назовем коэффициентом разбиения
) назовем коэффициентом разбиения 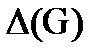 графа G :
графа G :
 . (2.12)
. (2.12)
Коэффициент разбиения 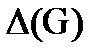 позволяет оценивать качество разбиения графа на куски, а также сравнивать различные алгоритмы разбиения графов. Очевидно, что лучшим разбиениям для одного и того же графа соответствуют наибольшие значения
позволяет оценивать качество разбиения графа на куски, а также сравнивать различные алгоритмы разбиения графов. Очевидно, что лучшим разбиениям для одного и того же графа соответствуют наибольшие значения 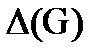 .
.
Существует значительное количество алгоритмов компоновки, которые можно условно разбить на пять групп: 1) последовательные алгоритмы; 2) итерационные алгоритмы; 3) алгоритмы, использующие методы целочисленного программирования; 4) алгоритмы, основанные на решении задачи о назначении; 5) смешанные алгоритмы.
|
|
|
1. Ввод матрицы 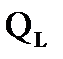 .
.
2. По матрице 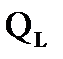 определяем локальные степени вершин
определяем локальные степени вершин 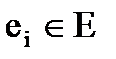 :
:
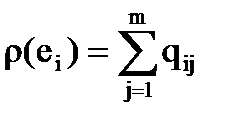 .
.
3. Из множества нераспределенных вершин E выбираем вершину 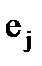 с локальной степенью
с локальной степенью 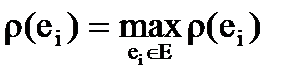 .
.
4. Назначаем выбранную вершину 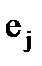 во множество
во множество 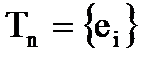 , формируемого узла.
, формируемого узла.
5. Строку 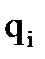 матрицы
матрицы 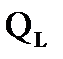 , соответствующую назначенной вершине
, соответствующую назначенной вершине 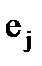 , модифицируем путем поразрядной дизъюнкции со строками матрицы, соответствующими нераспределенным элементам:
, модифицируем путем поразрядной дизъюнкции со строками матрицы, соответствующими нераспределенным элементам:
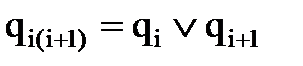 ;
; 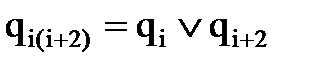 ;…
;…
6. Определяем суммы элементов 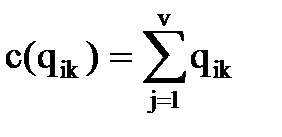 в модифицированных строках
в модифицированных строках 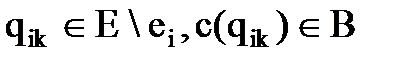 .
.
7. Из множества строк 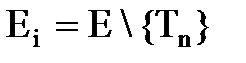 выбираем такие, в которых
выбираем такие, в которых 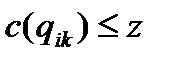 . Объединяем их во множество
. Объединяем их во множество  .
.
8. Если 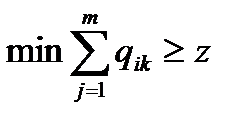 , то переходим к 17, иначе к 9.
, то переходим к 17, иначе к 9.
9. Строку  матрицы
матрицы  , соответствующую элементу
, соответствующую элементу 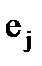 , модифицируем путем поразрядной конъюнкции со строками множества
, модифицируем путем поразрядной конъюнкции со строками множества  :
:
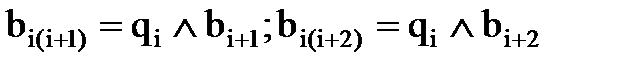 ;…
;…
10. Определяем суммы 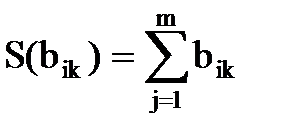 элементов в модифицированных строках
элементов в модифицированных строках 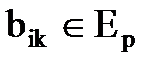 .
.
11. Из множества строк  выбираем такую, в которой
выбираем такую, в которой 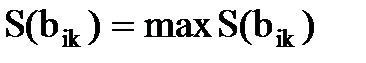 .
.
12. Вершину 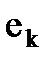 , дающую
, дающую 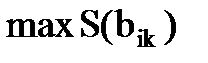 назначаем в формируемый узел
назначаем в формируемый узел 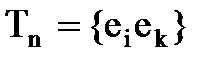 .
.
13. Если 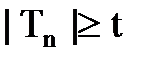 , то идти к 17, иначе к 14.
, то идти к 17, иначе к 14.
14. Определяем множество нераспределенных элементов 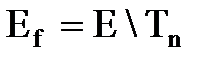 . Если
. Если 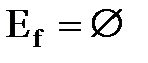 , то идти к 19, иначе к 15.
, то идти к 19, иначе к 15.
15. Составляем матрицу 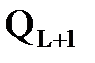 . Для чего в исходной матрице
. Для чего в исходной матрице 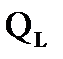 вместо строк, соответствующих элементам, назначенным в узел
вместо строк, соответствующих элементам, назначенным в узел 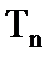 , записываем дизъюнкцию всех указанных строк.
, записываем дизъюнкцию всех указанных строк.
16. Идти к 5.
17. Узел 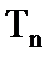 считаем сформированным. Поэтому преобразуем матрицу
считаем сформированным. Поэтому преобразуем матрицу 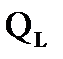 . Исключаем из нее строки, соответствующие элементам, включенным в узел
. Исключаем из нее строки, соответствующие элементам, включенным в узел 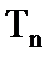 . Получаем матрицу
. Получаем матрицу 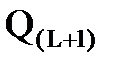 .
.
18. Идти к 2.
19. Конец.
Ручной расчет
1) Граф схемы
1 2 3 4
5 6 7 8
11
9 10 12
2) Составляем матрицу
1 2 3 4 5 6 7 8 9 10 11 12
1 0 1 0 0 1 0 0 0 0 0 0 0 2
2 1 0 0 0 0 1 1 0 0 0 0 0 3
3 0 0 0 2 0 0 0 0 0 0 0 0 2
4 0 0 2 0 0 0 1 0 0 0 0 0 3
5 1 0 0 0 0 0 0 0 1 1 0 0 3
6 0 1 0 0 0 0 1 0 0 0 1 0 3
7 0 1 0 1 0 1 0 0 0 0 0 0 3
8 0 0 0 0 0 0 0 0 0 0 1 1 2
9 0 0 0 0 1 0 0 0 0 2 0 0 3
10 0 0 0 0 1 0 0 0 2 0 0 0 3
11 0 0 0 0 0 1 0 0 0 0 0 0 2
12 0 0 0 0 0 0 0 1 0 0 0 0 1
Максимальную локальную степень, равную трем, имеют вершины С2,С4,С5,С6,С7,С9,С10. В качестве исходной выбираем 2-ю по порядку. Выполним дизъюнкции 2-й строки 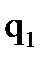 , соответствующей
, соответствующей 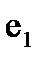 , с остальными строками.
, с остальными строками.
2 1 0 0 0 0 1 1 0 0 0 0 0
1 0 1 0 0 1 0 0 0 0 0 0 0
2˅1 1 1 0 0 1 1 1 0 0 0 0 0
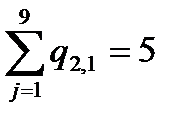
2 1 0 0 0 0 1 1 0 0 0 0 0
3 0 0 0 2 0 0 0 0 0 0 0
2˅3 1 0 0 2 0 1 1 0 0 0 0 0
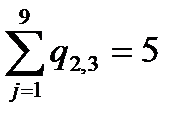
2 1 0 0 0 0 1 1 0 0 0 0 0
4 0 0 02 0 0 1 0 0 0 0 0
2˅4 1 0 2 0 0 1 1 0 0 0 0 0
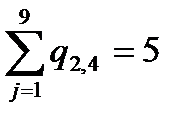
2 1 0 0 0 0 1 1 0 0 0 0 0
5 1 0 02 0 0 0 0 1 1 0 0
2˅5 1 0 0 0 0 1 1 0 1 1 0 0
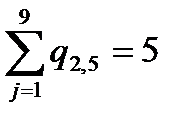
2 1 0 0 0 0 1 1 0 0 0 0 0
6 0 1 0 0 0 0 1 0 0 0 1 0
2˅6 1 1 0 0 0 1 1 0 0 0 1 0
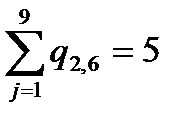
2 1 0 0 0 0 1 1 0 0 0 0 0
7 0 1 0 1 0 1 0 0 0 0 0 0
2˅7 1 1 0 1 0 1 1 0 0 0 0 0
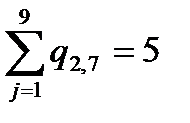
2 1 0 0 0 0 1 1 0 0 0 0 0
8 0 0 0 0 0 0 0 0 0 0 1 1
2˅8 1 0 0 0 0 1 1 0 0 0 1 1
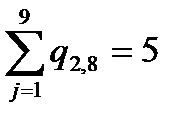
2 1 0 0 0 0 1 1 0 0 0 0 0
9 0 0 0 0 1 0 0 0 0 2 0 0
2˅9 1 0 0 0 1 1 1 0 0 2 0 0

2 1 0 0 0 0 1 1 0 0 0 0 0
1 0 0 0 0 0 1 0 0 0 2 0 0 0
2˅10 1 0 0 0 1 1 1 0 2 0 0 0
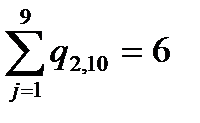
2 1 0 0 0 0 1 1 0 0 0 0 0
1 1 0 0 0 0 0 1 0 1 0 0 0 0
2˅11 1 0 0 0 0 1 0 1 0 0 0 0
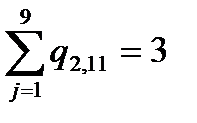
2 1 0 0 0 0 1 1 0 0 0 0 0
1 2 0 0 0 0 0 0 0 1 0 0 0 0
2˅12 1 0 0 0 0 1 1 1 0 0 0 0

Итак, выбираем вершины С3,С4,С5,С6,С7,С8,С11,С12,С1 Далее выполняем коньюнкцию с выбранными вершинами и 2-ой строкой.
2 1 0 0 0 0 1 1 0 0 0 0 0
1 0 1 0 0 1 0 0 0 0 0 0 0
2˄1 0 0 0 0 0 0 0 0 0 0 0 0
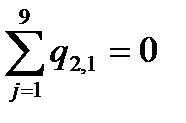
2 1 0 0 0 0 1 1 0 0 0 0 0
3 0 0 0 2 0 0 0 0 0 0 0
2˅3 0 0 0 2 0 0 0 0 0 0 0 0
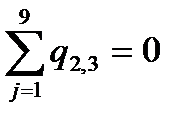
Тоже проделываем с остальными веришинами. Вычисляем суммы элементов в конъюнкциях. Выбираем вершину 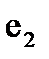 , величина S у которой максимальна, и включаем ее в узел T1. Если не удается найти все элементы,то модифицируем матрицу, и проделываем операции заново.Исходя из полученного Выбираем 4 элемента, для того чтобы “зашить их в ИМС Т1” Например С12,С8,С1,С2 число связей при этом минимально.
, величина S у которой максимальна, и включаем ее в узел T1. Если не удается найти все элементы,то модифицируем матрицу, и проделываем операции заново.Исходя из полученного Выбираем 4 элемента, для того чтобы “зашить их в ИМС Т1” Например С12,С8,С1,С2 число связей при этом минимально.
Сравним результаты с результатом компоновки прикладных программ САПР
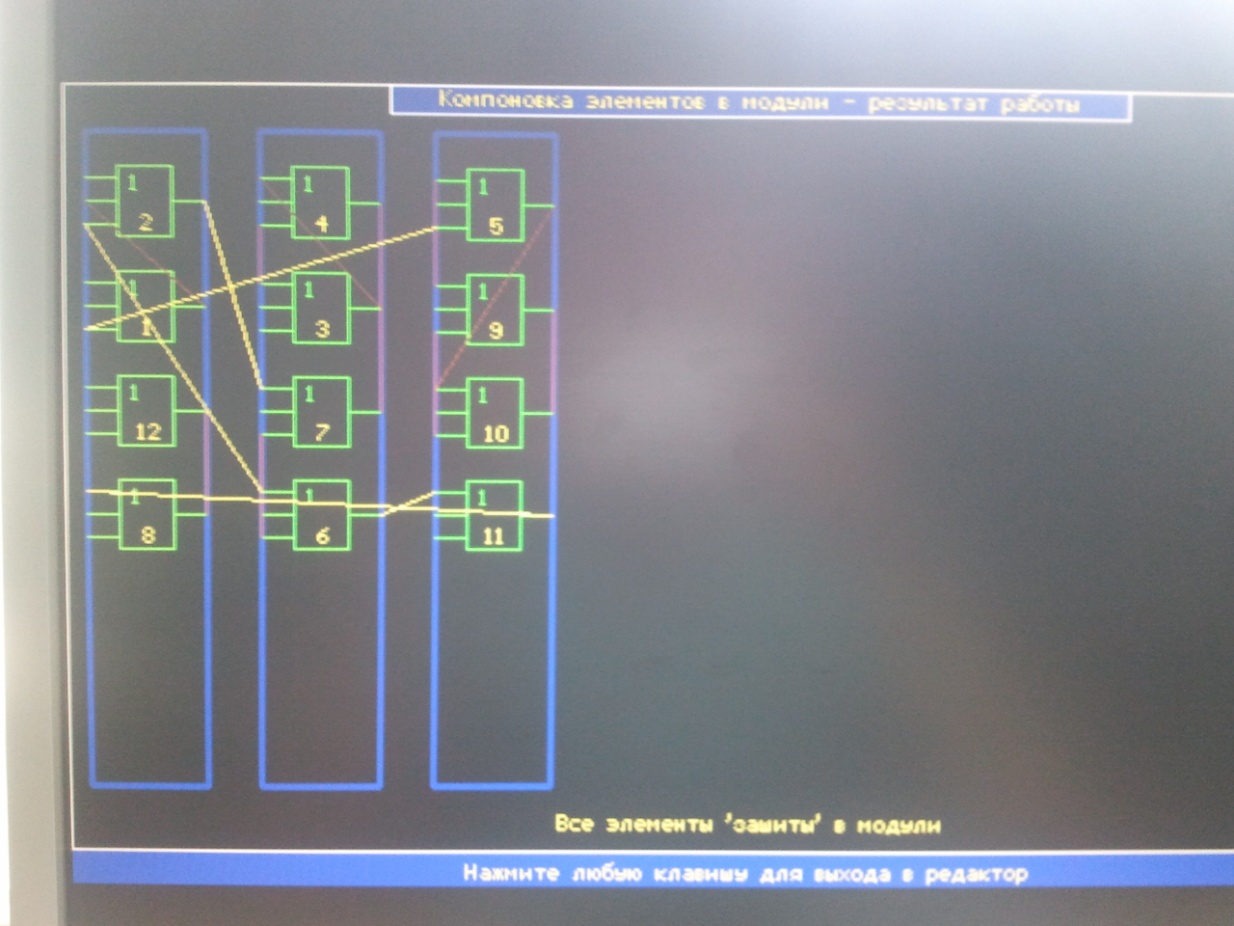
Рис3. Результат компоновки ПП САПР.
Результат компоновки элементов исходной схемы в блоки.
Результаты. Благодаря ручному расчету,мы убедились в правильной компоновке элементов в модули программой, получили данные и возможые варианты комплектования модулей по 4 элемента.
Выводы
Достоинствами последовательных алгоритмов компоновки по связанности являются их простота реализации на ЭВМ и высокое быстродействие. Кроме этого, они позволяют легко учитывать дополнительные ограничения на компоновку: несовместимость отдельных элементов в узле, априорно заданное функциональное распределение некоторых элементов схемы и др.
Недостатком этих алгоритмов является локальный пошаговый характер оптимизации, приводящий к тому, что в начале процесса выделяются сильно связанные группы элементов, в то время как в последние узлы попадают мало связанные или вообще не связанные элементы. При жестких ограничениях на число выводов это приводит к увеличению числа узлов.
Поэтому эффективность таких алгоритмов выше при компоновке узлов с небольшим отношением числа элементов к числу выводов (печатных плат, панелей и т. д.). Кроме этого, результаты лучше для схем с относительно невысокой связанностью.
Лабораторная работа №3
Дата добавления: 2019-07-17; просмотров: 286; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
