Волновая функция и ее статический смысл. Условие нормировки волновой функции.
С учетом наличия у микрочастицы волновых свойств ее состояние в квантовой механике задается с помощью некоторой функции координат и времени 
( x , y , z , t), называемой волновой или 
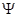- функцией.
Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения решения в частных физических задачах. Таким уравнением является уравнение Шрёдингера.
Теория, описывающая движение малых частиц с учетом их волновых свойств, называется квантовой, или волновой механикой. Квантовая механика в своей области (строение и свойства атомов, молекул и отчасти атомных ядер) прекрасно подтверждается опытом.
Волновая функция описывает состояние частицы во всех точках пространства и для любого момента времени. Для понимания физического смысла волновой функции обратимся к опытам по дифракции электронов. (Опыты Томсона и Тартаковского по пропусканию электронов через тонкую металлическую фольгу). Четкие дифракционные картины обнаруживаются даже в том случае, если направлять на мишень одиночные электроны, т.е. когда каждый последующий электрон испускается после того, как предыдущий достигнет экрана. После достаточной продолжительной бомбардировки картина на экране будет в точности соответствовать той, которая получается при одновременном направлении на мишень большого числа электронов.
|
|
|
Из этого можно сделать вывод о том, что движение любой микрочастицы по отдельности, в том числе и место ее обнаружения, подчиняется статистическим (вероятностным) закономерностям, и при направлении на мишень одиночного электрона точку на экране, в которой он будет зафиксирован, заранее со 100%-й уверенностью предсказать невозможно.
В дифракционных опытах Томсона на фотопластинке образовывалась система темных концентрических колец. Можно с уверенностью сказать, что вероятность обнаружения (попадания) каждого испущенного электрона в различных местах фотопластинки неодинакова. В области темных концентрических колец эта вероятность больше, чем в остальных местах экрана. Распределение электронов по всему экрану оказывается таким же, каким является распределение интенсивности электромагнитной волны в аналогичном дифракционном опыте: там, где интенсивность рентгеновской волны велика, частиц в опыте Томсона регистрируется много, а там, где интенсивность мала -- частицы почти не появляются.
С волновой точки зрения наличие максимума числа электронов в некоторых направлениях означает, что эти направления соответствуют наибольшей интенсивности волны де Бройля. Это послужило основанием для статистического (вероятностного) истолкования волны де Бройля.
|
|
|
Для одномерного движения (например, в направлении оси Ox) вероятность dP обнаружения частицы в промежутке между точками x и x + dx в момент времени t равна dP = 
где |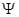 
(x , t)|2= 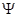( x , t) 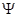*(x , t) - квадрат модуля волновой функции (значок * обозначает комплексное сопряжение).
В общем случае при движении частицы в трехмерном пространстве вероятность dP обнаружения частицы в точке с координатами ( x , y ,z) в пределах бесконечно малого объема dV задается аналогичным уравнением: dP =| 
( x , y , z , t )|2 dV.
Вероятность обнаружить частицу во всем бесконечном пространстве равна единице. Отсюда следует условие нормировки волновой функции:
.
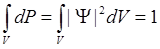Величина 
является плотностью вероятности, или плотностью распределение координат частиц. В простейшем случае одномерного движения частицы вдоль оси ОX среднее значение ее координаты вычисляется следующим соотношением:
|
|
|
<x ( t)> =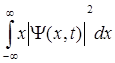 
.
Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна удовлетворять ряду ограничительных условий. Функция Ψ, характеризующая вероятность обнаружения микрочастицы в элементе объема, должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной), непрерывной (вероятность не может меняться скачком) и гладкой (без изломов) во всем пространстве.
Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями Ψ1, Ψ2 , … Ψn , то она может находиться в состоянии, описываемом линейной комбинацией этих функций:
,
где Cn (n = 1, 2, 3…) – произвольные, вообще говоря, комплексные числа.
Среднее расстояние < r > электрона отядра вычисляется по формуле:
.
Таким образом, точно предсказать в дифракционных опытах, в каком месте экрана будет зафиксирован тот или иной электрон, невозможно, даже заранее зная его волновую функцию. Можно лишь с определенной вероятностью предположить, что электрон будет зафиксирован в определенном месте.
|
|
|
Де Бройль использовал представление о фазовых волнах (волнах вещества или волнах де Бройля) для наглядного толкования правила квантования орбит электрона в атоме по Бору в случае одноэлектронного атома. Он рассмотрел фазовую волну, бегущую вокруг ядра по круговой орбите электрона. Если на длине орбиты укладывается целое число этих волн 
, то волна при обходе вокруг ядра будет всякий раз возвращаться в исходную точку с той же фазой и амплитудой. В этом случае орбита становится стационарной и не возникает излучения. Де Бройль записал условие стационарности орбиты или правило квантования в виде:
,
где r – радиус круговой орбиты, п – целое число (главное квантовое число). Полагая здесь 
и учитывая, что p есть модуль имрульса, а L = rp есть модуль момента импульса электрона, получим: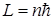 
,
что совпадает с правилом квантования орбит электрона в атоме водорода по Бору. Однако, в рассуждениях де Бройля предполагалось, что волна распространяется не в пространстве, а вдоль линии – вдоль стационарной орбиты электрона. Этим приближением можно пользоваться в предельном случае, когда длина волны 
пренебрежимо мала по сравнению с радиусом орбиты электрона.
Дата добавления: 2019-07-17; просмотров: 762; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!