Программирование функции формулы Ньютона
Аннотация
Пояснительная записка курсовой работы "Интерполяция функции одной переменной методом Ньютона" содержит в себе введение, анализ задания описанием входных и выходных данных, обзор литературных источников, описание математической модели и методов вычислительной математики, пояснения к алгоритму, текст программы, инструкцию. При изучении дисциплины "Информатика" для написания курсовой работы использовались различные литературные источники, которые перечислены в настоящем документе. В данной курсовой работе приведена программа, которая применяется для интерполяции таблично заданной функции методом Ньютона. В ней был использован метод структурного программирования для облегчения написания и отладки программы, а также повышения ее наглядности и читаемости. Целью написания данной работы было получение и закрепление практических навыков разработки алгоритмов различными методами. Представленная программа реализована на языке программирования Pascal. Пояснительная записка содержит 25 листов, на которых размещено два рисунка, текст программы и описание программы и алгоритма.
Содержание
Введение
Анализ задания
Математическая модель задачи
Программирование функции формулы Ньютона
Обзор литературных источников
Разработка программы по схеме алгоритма
Инструкция пользования программой
Текст программы
Исходные данные и результат решения контрольного примера
Заключение
Список использованных источников
Введение
Современное развитие физики и техники тесно связано с использованием электронных вычислительных машин (ЭВМ). В настоящее время ЭВМ стали обычным оборудованием многих институтов и конструкторских бюро. Это позволило от простейших расчетов и оценок различных конструкций или процессов перейти к новой стадии работы - детальному математическому моделированию (вычислительному эксперименту), которое существенно сокращает потребность в натурных экспериментах, а в ряде случаев может их заменить.
Сложные вычислительные задачи, возникающие при исследовании физических и технических проблем, можно разбить на ряд элементарных -таких как вычисление интеграла, решение дифференциального уравнения и т. п. Многие элементарные задачи являются несложными и хорошо изучены. Для этих задач уже разработаны методы численного решения, и нередко имеются стандартные программы решения их на ЭВМ. Есть и достаточно сложные элементарные задачи; методы решения таких задач сейчас интенсивно разрабатываются.
В связи с этим современный специалист с высшим образованием должен обладать не только высоким уровнем подготовки по профилю своей специальности, но и хорошо знать математические методы решения инженерных задач, ориентироваться на использование вычислительной техники, практически освоить принципы работы на ЭВМ.
Анализ задания
В качестве входных данных использованы:
1. Количество узлов.
2. Табличные значения функции.
Выходными данными, т.е. результатом программы является:
1. Значения таблично заданной функции в промежуточных значениях.
2. График полинома.
Математическая модель задачи
При выполнении курсовой работы была выбрана следующая математическая модель:
Интерполяция и приближение функций.
1. Постановка задачи.
Одной из основных задач численного анализа является задача об интерполяции функций. Часто требуется восстановить функцию  для всех значений
для всех значений  на отрезке
на отрезке 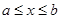 если известны ее значения в некотором конечном числе точек этого отрезка. Эти значения могут быть найдены в результате наблюдений (измерений) в каком-то натурном эксперименте, либо в результате вычислений. Кроме того, может оказаться, что функция
если известны ее значения в некотором конечном числе точек этого отрезка. Эти значения могут быть найдены в результате наблюдений (измерений) в каком-то натурном эксперименте, либо в результате вычислений. Кроме того, может оказаться, что функция  задается формулой и вычисления ее значений по этой формуле очень трудоемки, поэтому желательно иметь для функции более простую (менее трудоемкую для вычислении) формулу, которая позволяла бы находить приближенное значение рассматриваемой функции с требуемой точностью в любой точке отрезка. В результате возникает следующая математическая задача.
задается формулой и вычисления ее значений по этой формуле очень трудоемки, поэтому желательно иметь для функции более простую (менее трудоемкую для вычислении) формулу, которая позволяла бы находить приближенное значение рассматриваемой функции с требуемой точностью в любой точке отрезка. В результате возникает следующая математическая задача.
Пусть и» отрезке 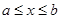 задана сетка со
задана сетка со

и в ее узлах заданы значения функции  , равные
, равные
 .
.
Требуется построить интерполянту — функцию  , совпадающую с функцией
, совпадающую с функцией  в узлах сетки:
в узлах сетки:

 .
.
Основная цель интерполяции — получить быстрый (экономичный) алгоритм вычисления значений  для значений
для значений  , не содержащихся в таблице данных.
, не содержащихся в таблице данных.
2. Интерполяция по Ньютону
Дана табличная функция:
| i | 
| 
|
| 0 | 
| 
|
| 1 | 
| 
|
| 2 | 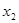
| 
|
| .. | .. | .. |
| n | 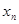
| 
|
Или
 ,
, 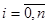 (1)
(1)
Точки с координатами  называются узловыми точками или узлами.
называются узловыми точками или узлами.
Количество узлов в табличной функции равно N=n+1.
Необходимо найти значение этой функции в промежуточной точке, например,  , причем
, причем  . Для решения задачи используется интерполяционный многочлен.
. Для решения задачи используется интерполяционный многочлен.
Интерполяционный многочлен по формуле Ньютона имеет вид:

где n – степень многочлена,
Интерполяционная формула Ньютона формула позволяет выразить интерполяционный многочлен  через значение
через значение  в одном из узлов и через разделенные разности функции
в одном из узлов и через разделенные разности функции  , построенные по узлам
, построенные по узлам  .
.
Сначала приведем необходимые сведения о разделенных разностях.
Пусть в узлах
 ,
, 
известны значения функции  . Предположим, что среди точек
. Предположим, что среди точек  ,
,  , нет совпадающих. Разделенными разностями первого порядка называются отношения
, нет совпадающих. Разделенными разностями первого порядка называются отношения
 ,
,  ,
,  .
.
Будем рассматривать разделенные разности, составленные по соседним узлам, т. е. выражения
 .
.
По этим разделенным разностям первого порядка можно построить разделенные разности второго порядка:
 ,
,
 ,
,

Таким образом, разделённая разность  -го порядка на участке
-го порядка на участке  может быть определена через разделённые разности
может быть определена через разделённые разности  -го порядка по рекуррентной формуле:
-го порядка по рекуррентной формуле:
 . (3)
. (3)
где  ,
,  ,
, 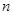 - степень многочлена.
- степень многочлена.
Максимальное значение  равно
равно 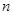 . Тогда
. Тогда 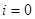 и разделенная разность n-го порядка на участке
и разделенная разность n-го порядка на участке  равна
равна
 ,
,
т.е. равна разности разделенных разностей  -го порядка, разделенной на длину участка
-го порядка, разделенной на длину участка  .
.
Разделенные разности
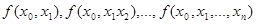
являются вполне определенными числами, поэтому выражение (1) действительно является алгебраическим многочленом  -й степени. При этом в многочлене (1) все разделенные разности определены для участков
-й степени. При этом в многочлене (1) все разделенные разности определены для участков  ,
,  .
.
При вычислении разделенных разностей принято записывать их в виде таблицы

| 
| ||||

| |||||

| 
| 
| |||

| • | ||||

| 
| • | • | • | 
|
| ■ | • | • | • | ||
| • | • | • | 
| ||
| • | • | 
| |||

| 
|
Разделенная разность  -го порядка следующим образом выражается через значения функции
-го порядка следующим образом выражается через значения функции  в узлах:
в узлах:
 . (1)
. (1)
Эту формулу можно доказать методом индукции. Нам потребуется частный случай формулы (1):

Интерполяционным многочленом Ньютона называется многочлен

Рассмотренная форма полинома Ньютона носит название первой интерполяционной формулы Ньютона, и используется, обычно, при интерполировании вначале таблицы.
Заметим, что решение задачи интерполяции по Ньютону имеет некоторые преимущества по сравнению с решением задачи интерполяции по Лагранжу. Каждое слагаемое интерполяционного многочлена Лагранжа зависит от всех значений табличной функции yi, i=0,1,…n. Поэтому при изменении количества узловых точек N и степени многочлена n (n=N-1) интерполяционный многочлен Лагранжа требуется строить заново. В многочлене Ньютона при изменении количества узловых точек N и степени многочлена n требуется только добавить или отбросить соответствующее число стандартных слагаемых в формуле Ньютона (2). Это удобно на практике и ускоряет процесс вычислений.
Программирование функции формулы Ньютона
Для построения многочлена Ньютона по формуле (1) организуем циклический вычислительный процесс по  . При этом на каждом шаге поиска находим разделенные разности k-го порядка. Будем помещать разделенные разности на каждом шаге в массив Y.
. При этом на каждом шаге поиска находим разделенные разности k-го порядка. Будем помещать разделенные разности на каждом шаге в массив Y.
Тогда рекуррентная формула (3) будет иметь вид:

 (4)
(4)

В формуле Ньютона (2) используются разделенные разности  -го порядка, подсчитанные только для участков
-го порядка, подсчитанные только для участков  т.е. разделенные разности
т.е. разделенные разности  -го порядка для
-го порядка для  . Обозначим эти разделенные разности k-го порядка как
. Обозначим эти разделенные разности k-го порядка как  . А разделенные разности, подсчитанные для
. А разделенные разности, подсчитанные для  , используются для расчетов разделенных разностей более высоких порядков.
, используются для расчетов разделенных разностей более высоких порядков.
Используя (4), свернем формулу (2). В результате получим
 (5)
(5)
где
 – значение табличной функции (1) для
– значение табличной функции (1) для  .
.
 – разделенная разность
– разделенная разность  -го порядка для участка
-го порядка для участка  .
.
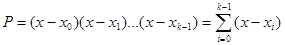 .
.
Для вычисления Р удобно использовать рекуррентную формулу  внутри цикла по
внутри цикла по  .
.
Схема алгоритма интерполяции по Ньютону представлена на рисунке:

Function POlinom(n: integer; d:real; x,y :per):real;
var
l:real;
k,i:integer;
p: real;
begin
L:=y[0];
P:=1;
for k:=1 to n do begin
P:=P*(D-X[k-1]);
for i:=0 to (n-k) do begin
Y[i]:=(y[i+1]-y[i])/(x[i+k]-x[i]);
end;
L:=L+P*y[0];
end;
Polinom:=l;
end;
где
n – количество узлов
x[i],y[i] – табличные значения функции
D – точка, в которой необходимо вычислить значение l
Дата добавления: 2019-07-15; просмотров: 224; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
