Розв’язати в цілих числах рівняння
 .
.
Розв'язок.
Перепишемо дане рівняння у вигляді :
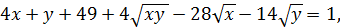
Або
 ,
,
Звідки
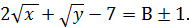
Таким чином дане рівняння розпадається на два :
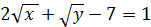

Або
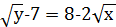 (1)
(1)
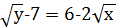 (2)
(2)
Так як 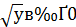 , то в (1) невідомий корінь 𝑥 може набувати цілі значення 0, 1, 4, 9, 16, а в (2) – лише цілі значення 0, 1, 4, 9. Відповідні їм значення 𝑦 такі: 64, 36, 16, 4, 0; 36, 16, 4, 0. Отже дане рівняння має 9 розв’язків в цілих числах.
, то в (1) невідомий корінь 𝑥 може набувати цілі значення 0, 1, 4, 9, 16, а в (2) – лише цілі значення 0, 1, 4, 9. Відповідні їм значення 𝑦 такі: 64, 36, 16, 4, 0; 36, 16, 4, 0. Отже дане рівняння має 9 розв’язків в цілих числах.
Відповідь: 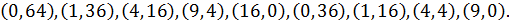
Приклад 7.
Розв’язати в цілих числах рівняння
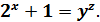
Розв'язок.
Очевидно, що 𝑥 та 𝑧 не можуть бути від’ємними числами, так як при 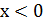
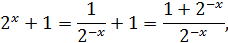
а тому 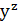 має вигляд
має вигляд 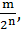 що можливо лише при парних значеннях 𝑦. Але з умови випливає, що 𝑦 не може бути парним числом, якщо
що можливо лише при парних значеннях 𝑦. Але з умови випливає, що 𝑦 не може бути парним числом, якщо  .
.
Якщо  , то рівняння має вигляд
, то рівняння має вигляд
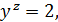
звідки 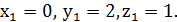
Нехай  Маємо
Маємо
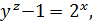
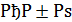
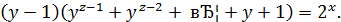
Із цього рівняння випливає, що
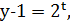 або
або 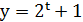 , де 𝑡 – натуральне число.
, де 𝑡 – натуральне число.
Оскільки 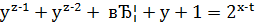 і оскільки 𝑦 – непарне число, то 𝑧 – парне число або
і оскільки 𝑦 – непарне число, то 𝑧 – парне число або  .
.
Нехай 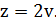 Тоді
Тоді 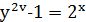 , або
, або  , звідки
, звідки
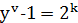 ,
, 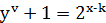 . Тому
. Тому 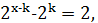 або
або  тобто
тобто 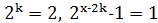 , звідки
, звідки 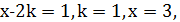 і тому
і тому 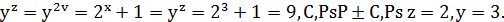
Якщо ж  , то 𝑥 довільне, 𝑎 𝑦
, то 𝑥 довільне, 𝑎 𝑦 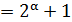 . І так, при
. І так, при 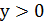 ми маємо, крім тривіального розв'язку
ми маємо, крім тривіального розв'язку 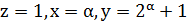 , де 𝛼 – будь яке натуральне число або нуль, лише ще один розв'язок:
, де 𝛼 – будь яке натуральне число або нуль, лише ще один розв'язок:
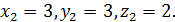
При  . Очевидно, що непарних значеннях z дане рівняння не має розв’язків , при парних значеннях z рівняння зводиться до вигляду:
. Очевидно, що непарних значеннях z дане рівняння не має розв’язків , при парних значеннях z рівняння зводиться до вигляду:
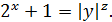
Отже, рівняння має тривіальний розв'язок 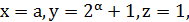 де 𝛼 – будь-яке натуральне число, і, крім того, ще має тільки три розв’язки:
де 𝛼 – будь-яке натуральне число, і, крім того, ще має тільки три розв’язки:
|
|
|

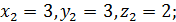
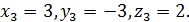
Приклад 8.
Розв’язати в натуральних числах рівняння
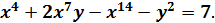
Розв'язок.
Перепишемо дане рівняння у вигляді:
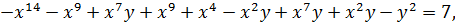
або
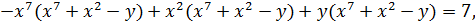
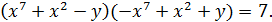
Оскільки дільниками числа 7 є лише числа 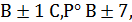 то шукані числа 𝑥 та 𝑦 треба шукати серед розв’язків наступних чотирьох систем:
то шукані числа 𝑥 та 𝑦 треба шукати серед розв’язків наступних чотирьох систем:
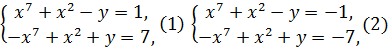

Перша система має єдиний розв'язок в натуральних числах 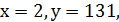 третя система має також єдиний розв'язок в натуральних числах
третя система має також єдиний розв'язок в натуральних числах 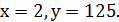 Друга та четверта системи не мають розв’язків в натуральних числах.Отже, дане рівняння має рівно два розв’язки в натуральних числах:
Друга та четверта системи не мають розв’язків в натуральних числах.Отже, дане рівняння має рівно два розв’язки в натуральних числах: 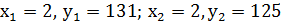 .
.
Приклад 9.
Розв’язати в цілих числах рівняння:
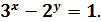
Розв'язок.
Ні одне із невідомих не може бути цілим від’ємним числом, так як рівності
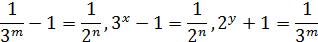
неможливі при натуральних 𝑥, 𝑦, 𝑚, 𝑛.
Легко перевірити, що 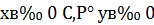 . Отже, 𝑥, 𝑦 – натуральні. Із умови випливає:
. Отже, 𝑥, 𝑦 – натуральні. Із умови випливає:
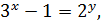
або 
або 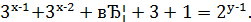
Число 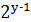 – парне, якщо
– парне, якщо 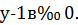
Якщо 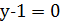 , то
, то 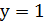 , а тому із умови маємо
, а тому із умови маємо
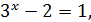
тобто, 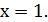
Таким чином, 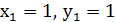 - розв'язок даного рівняння.
- розв'язок даного рівняння.
Якщо ж 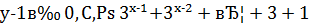 повинно містити парну кількість доданків, а тому 𝑥 – парне число; нехай
повинно містити парну кількість доданків, а тому 𝑥 – парне число; нехай 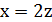 . Тоді
. Тоді
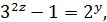
або 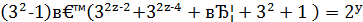 ,
,
або  .
.
Якщо 𝑧 – непарне число, то 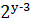 - непарне число, що можливо лише при
- непарне число, що можливо лише при  тобто
тобто  .
.
|
|
|
Тоді з умови маємо
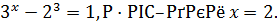
тому 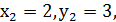 - другий розв'язок даного рівняння.
- другий розв'язок даного рівняння.
Якщо ж 𝑧 – парне число, тобто  , то
, то 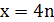 , а тому дане рівняння перепишемо у вигляді:
, а тому дане рівняння перепишемо у вигляді:
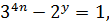
або 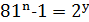 ;
;
тому 
останнє рівняння не має розв’язків, так як 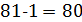 ділиться на 5, а
ділиться на 5, а 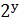 не ділиться на 5.
не ділиться на 5.
Відповідь: (1, 1), (2, 3).
Приклад 10.
Розв’язати в натуральних числах рівняння:
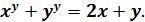
Розв'язок.
Перепишемо рівняння у такому вигляді:
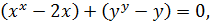
 (1)
(1)
Якщо 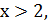 то
то 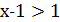 , а тому
, а тому  , тобто
, тобто 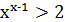 ; відповідно, при
; відповідно, при  має місце нерівність
має місце нерівність
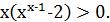 (2)
(2)
Якщо 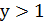 , то
, то 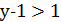 , а тому
, а тому  ; значить, при
; значить, при 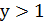 має місце нерівність
має місце нерівність
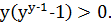 (3)
(3)
Об’єднуючи нерівності (2) і(3), отримуємо, що при 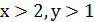 ліва частина рівняння (1) додатна і тому відмінна від нуля.
ліва частина рівняння (1) додатна і тому відмінна від нуля.
Отже, при існуванні цілих додатних чисел даного рівняння 𝑥 має дорівнювати 1 або 2, а 𝑦 = 1. Підстановкою впевнюємось, що лише 𝑥 = 2, 𝑦 = 1 є розв’язком даного рівняння в натуральних числах.
Відповідь: (2, 1).
Приклад 11.
Дата добавления: 2019-07-15; просмотров: 207; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
