Об оценке сверху числа приведенных неопределенных бинарных квадратичных форм.
О числе приведенных неопределенных бинарных квадратичных форм, так и о числе классов неопределенных квадратичных форм известно очень мало. Для числа классов бинарных квадратичных форм имеется точная формула Дирихле. Другим важным результатом являются неравенства, принадлежащие немецкому математику Зигелю.
,
где 
- число приведенных неопределенных бинарных квадратичных форм дискриминанта 
; 
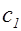и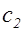 
- положительные постоянные, зависящие от 
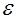; причем 
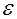- любое фиксированное положительное число. Наша цель состоит в том, чтобы элементарным способом доказать верхнюю оценку в неравенствах Зигеля для . Приводимое доказательство будет опираться на некоторые свойства функции числа положительных делителей натурального числа и мы их приведем вначале.
Арифметическая функция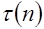 
определяется как число положительных делителей натурального числа 
.
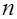Предложение 1. Функция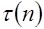 
мультипликативна, т.е. 
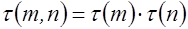, если 
.
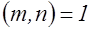Из этого предложения 1 легко выводится следующее
Предложение 2. Если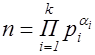 
- каноническое разложение натурального числа 
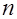, то
.
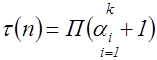Доказательства предложений 1 и 2 приводятся во всех учебниках по теории чисел (напр. см. [4,6]).
Предложение 3. Для числа 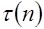делителя натурального числа имеет место неравенство
.
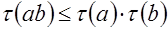Доказательство. Пусть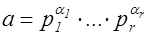 
и 
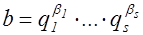- канонические разложения чисел 
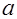и 
, и пусть
, 
,…, 
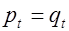- все простые делители наибольшего общего делителя чисел 
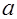и . Тогда ясно, что
|
|
|
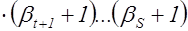. (1)
Но так как справедливо неравенство
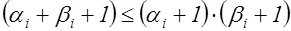
, (2)
то неравенство (1) с учетом (2) и предложения 2 перейдет в следующие соотношения
.
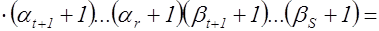
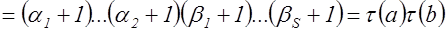Предложение 3 доказано.
Предложение 4. Для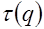 
имеет место неравенство
,
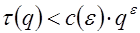где 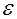- произвольное положительное число, 
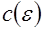- постоянная, зависящая только от .
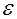Доказательство. Мы следуем рассуждениям в [4,5] (доказательство имеется также в [3]). Пусть 
- каноническое разложение числа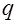 
. Тогда имеем
.
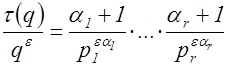Рассмотрим отношение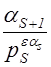 
, в случаях 
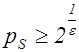и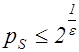 
.
Если 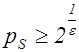, то 
, так как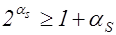 
.
Если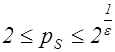 
, то считая 
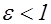, получим
.
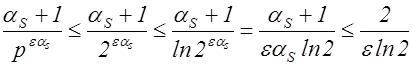Поэтому
.
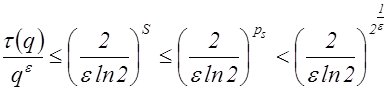Следовательно, полагая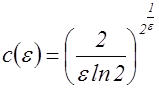 
, получим неравенство
.
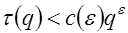Предложение 4 доказано.
Следующее предложение характеризует среднее значение 
в нужной для нас форме.
Предложение 5. Для 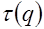имеет место следующая оценка сверху
,
где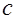 
- постоянная 
.
Доказательство. Имеем
.
Последняя сумма геометрически представляет собой число целых точек в первой четверти, лежащих на или под гиперболой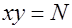 
, при этом целые точки, лежащие на осях координат исключаются, так как для них 
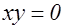. Поэтому исследуемую сумму можно записать в ви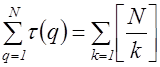де
|
|
|
, где 
- целая часть числа 
.
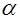Оцениваем теперь сумму
,
где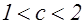 
.
Здесь мы воспользовались следующим соотношением из математического анализа
,
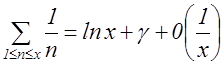где
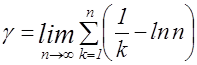
есть так называемая постоянная Эйлера.
Предложение 5 доказано.
Перейдем теперь к элементарному доказательству следующего результата.
Теорема (Зигель). Для числа всех приведенных неопределенных бинарных квадратичных форм дискриминанта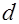 
справедливо неравенство
,
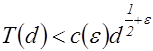где 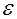- произвольное положительное число, 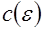- постоянная, зависящая только от 
.
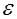Доказательство. Пусть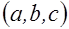 
- неопределенная приведенная форма дискриминанта 
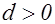. Тогда 
,
, 
.
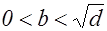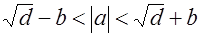Оценим сверху число приведенных форм с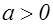 
и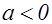 
. Тогда
.
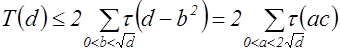Применяя к последней сумме предложения 3,4,5, получим
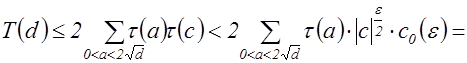
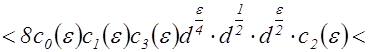
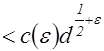, где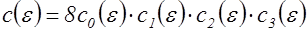 
.
Теорема доказана.
Дата добавления: 2019-07-15; просмотров: 110; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!