Эвклидовы и унитарные пространства

Определение 9. Симметрическая билинейная форма A(x, y) на вещественном пространстве (эрмитово-симметрическая форма на комплексном пространстве) называется положительно определенной, если A(x, x)>0 для любого, отличного от нуля вектора x из рассматриваемого пространства.

Определение 9 ¢. Квадратичная форма (эрмитова квадратичная форма) называется положительно определенной, если для любого вектора x¹0 она принимает положительное значение.

Определение 10. n-мерным эвклидовым (унитарным) пространством называется n-мерное вещественное (комплексное) векторное пространство с положительно определенным симметрическим (эрмитовым) скалярным произведением.

Все вводимые далее понятия пригодны как для эвклидовых, так и для унитарных пространств.

Определение 11. База e₁, e₂, …, e_n эвклидова (унитарного) пространства называется ортогональной, если (e_i, e_j)=0, i¹j, i, j=1, 2, …, n, и ортонормированной, если она ортогональна и длина всех векторов равны единице.

Изометрия эвклидовых и унитарных пространств

Определение 12. Взаимно однозначное отображение f модуля М на модуль М¢ над одним и тем же кольцом K называется изоморфизмом, если выполняются следующие условия:

 

1. f(x, y)=f(x)+f(y)=x¢+y¢; x¢=f(x); y¢=f(y);

"x, yÎM;

2. f(ax)=af(x)=ax¢; "xÎK; "xÎM; x¢=f(x)ÎM¢.

Определение 13. Два векторных пространства W и W¢ над полем Р называются изоморфными, если они изморфны как модули над кольцом, которым является поле Р.

Пусть теперь даны два векторных пространства W и W¢ со скалярными произведениями A(x, y) и A¢(x¢, y¢) над полем Р.

Определение 14. Изометрией векторных пространств W и W¢ называется любой их изморфизм, который сохраняет значения всех скалярных произведений, т. е.

A(x, y)= A¢(f(x), f(y))= A¢(x¢, y¢); "x, yÎW;

f(x)=x¢; f(y)=y¢.

 

В эвклидовом пространстве из определения длины вектора и угла между двумя векторами следует, что при изометрии сохраняются длины векторов и углы между ними, т. е. сохраняются метрические соотношения, чем и объясняется название «изометрия». В унитарном пространстве при изометрии сохраняются длины векторов, ортогональные векторы переходят в ортогональные векторы.

 

Матрицы

 

Линейные отображения, операторы и матрицы

Определение 1. Отображение f: V®W векторного пространства V в векторное пространство W над полем Р называется линейное отображение, если для всех v, v₁, v₂ÎV, aÎP выполняются условия:

 

1) f(v₁+v₂)=f(v₁)+f(v₂);

2) f(av)=af(v).

 

Если V=W, то линейное отображение называется линейным оператором или линейным преобразованием пространства V.

Пусть e₁, e₂, …, e_n – базис пространства V, а e₁¢, e₂¢, …, e_n¢ - базис пространства W. Образы базисных векторов пространства V в базисе пространства W можно записать в виде

 

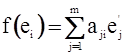 (i=1, 2, …, m) (1)

 

Коэффициенты в выражении (1) запишем в виде матрицы, которая называется матрицей линейного отображения f.

 

.

 

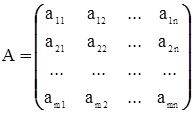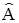В случае линейных операторов, т. е. линейных отображений векторного пространства в себя, операторы удобно обозначать , а матрицу оператора  в фиксированном базисе – в виде А.

---

Дата добавления: 2019-07-15; просмотров: 156; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!