Строение числовых НОД и НОК полугрупп
Далее будем рассматривать множество всех неотрицательных действительных чисел R + и мультипликативную полугруппу S 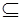 R +, содержащую 0 и 1, с топологией, индуцированной топологией числовой прямой.
R +, содержащую 0 и 1, с топологией, индуцированной топологией числовой прямой.
Лемма 1. Если S связно, то S =  или S =R +.
или S =R +.
Доказательство. Пусть S связное множество в R +. Тогда S является промежутком. Поскольку 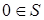 и
и 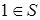 , то
, то  . Если в S нет элемента c > 1, то
. Если в S нет элемента c > 1, то  . В противном случае числа
. В противном случае числа 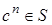 (
( 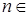 N) принимают сколь угодно большие значения. Поскольку S – промежуток, то
N) принимают сколь угодно большие значения. Поскольку S – промежуток, то 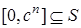 для всех
для всех  N. Отсюда
N. Отсюда 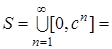 R +.
R +.
Лемма 2. Если  несвязно, то
несвязно, то 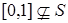 .
.
Доказательство. Предположим, что  .Тогда в силу несвязности
.Тогда в силу несвязности 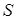 существуют такие числа
существуют такие числа 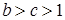 , что
, что 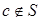 и
и 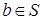 . Так как
. Так как 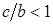 , то
, то 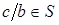 . Тогда
. Тогда 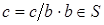 . Полученное противоречие завершает доказательство.
. Полученное противоречие завершает доказательство.
Лемма 3. Если 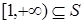 , то
, то 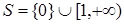 или
или  =R +.
=R +.
Доказательство. Очевидно, 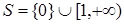 - полугруппа. Пусть
- полугруппа. Пусть 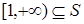 и
и 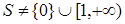 . Тогда существует элемент
. Тогда существует элемент 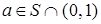 . Докажем, что
. Докажем, что 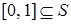 . Возьмем произвольное
. Возьмем произвольное 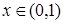 . Пусть натуральное N таково, что
. Пусть натуральное N таково, что 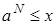 . Тогда из
. Тогда из 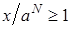 следует
следует 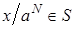 . Отсюда
. Отсюда 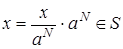 . Лемма доказана.
. Лемма доказана.
Лемма 4. Пусть S – НОД-полугруппа и пространство S несвязно. Тогда:
1) (0,с) 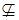 S для любого
S для любого 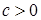 ,
,
2) если  , то и
, то и  для любого
для любого  .
.
Доказательство. 1) Если в интервале (0,1) нет элементов из S, то заключение очевидно. Пусть (0,1)ÇS¹Æ.Предположим, что (0,c)  S для некоторого
S для некоторого 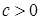 . Не теряя общности, будем считать, что
. Не теряя общности, будем считать, что  . Так как S несвязно, то по лемме 2 существует s
. Так как S несвязно, то по лемме 2 существует s 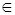 [0, 1]\S. Возьмем в S ненулевой элемент
[0, 1]\S. Возьмем в S ненулевой элемент 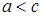 и положим b=as
и положим b=as 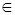 S . Пусть d =НОД(a , b). Поскольку 0<s<1, то sn
S . Пусть d =НОД(a , b). Поскольку 0<s<1, то sn 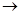 0 при n
0 при n 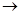
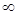 . Тогда sN < c для некоторого натурального N, и, значит, sN
. Тогда sN < c для некоторого натурального N, и, значит, sN 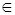 S. По свойству 8, пункт (3), НОД(a / d , b / d)=1. Поскольку b / d:a / d=s
S. По свойству 8, пункт (3), НОД(a / d , b / d)=1. Поскольку b / d:a / d=s  S, то элемент a / d необратим в S. Очевидно, необратимым является и (a / d)N. По свойству 11, пункт (5), имеем НОД((a / d)N, (b / d)N)=1. Из (b / d)N:((a / d)N=sN
S, то элемент a / d необратим в S. Очевидно, необратимым является и (a / d)N. По свойству 11, пункт (5), имеем НОД((a / d)N, (b / d)N)=1. Из (b / d)N:((a / d)N=sN 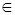 S следует, что НОД((a / d)N, (b / d)N)=(a / d)N. Значит, элемент (a / d)N ассоциирован с 1, т. е. обратим. Получили противоречие. Следовательно, (0, с)
S следует, что НОД((a / d)N, (b / d)N)=(a / d)N. Значит, элемент (a / d)N ассоциирован с 1, т. е. обратим. Получили противоречие. Следовательно, (0, с) 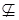 S для любого
S для любого 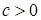 .
.
|
|
|
2) Если 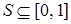 , то заключение справедливо. Пусть
, то заключение справедливо. Пусть 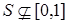 и
и 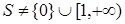 . Тогда по лемме 3 существует s
. Тогда по лемме 3 существует s 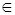
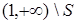 . Предположим, что
. Предположим, что 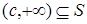 для некоторого с >1. Возьмем в S элемент
для некоторого с >1. Возьмем в S элемент  и положим b=as
и положим b=as 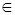 S . Поскольку s >1, то sn
S . Поскольку s >1, то sn 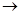 +¥ при n
+¥ при n 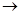
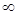 . Следовательно, sN>c для некоторого натурального N, и, значит, sN
. Следовательно, sN>c для некоторого натурального N, и, значит, sN 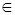 S. Повторяя рассуждения, проведенные выше, заключаем:
S. Повторяя рассуждения, проведенные выше, заключаем: 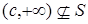 для любого
для любого 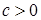 .
.
Предложение 2. Пусть S – НОД-полугруппа. Если пространство S несвязно и 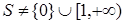 , то S нульмерно.
, то S нульмерно.
Доказательство. Докажем, что при выполненных условиях в любом интервале 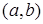 , где
, где 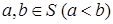 , есть точки, не принадлежащие S. Доказывая от противного, предположим, что [a,b]
, есть точки, не принадлежащие S. Доказывая от противного, предположим, что [a,b] 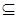 S для некоторых
S для некоторых 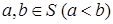 . Возможны два случая.
. Возможны два случая.
Случай 1. Пусть 0<a< 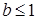 . Докажем, что найдется n0
. Докажем, что найдется n0 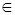 N, для которого a
N, для которого a 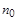
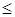 b
b 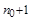 . В самом деле, допуская, что b
. В самом деле, допуская, что b 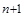 < a
< a 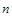 для всех n
для всех n 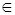 N и, переходя в неравенстве b
N и, переходя в неравенстве b 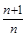 < a к пределу при n
< a к пределу при n 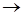
 , получили бы b
, получили бы b  a < b. Откуда b
a < b. Откуда b 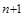 > a
> a 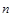 для всех натуральных n > n0. Тогда
для всех натуральных n > n0. Тогда 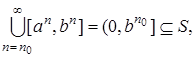 что невозможно по лемме 4.
что невозможно по лемме 4.
|
|
|
Случай 2. Пусть 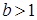 . Возьмем такое число с > a, чтобы 1<c<b. Рассуждая, как и в случае 1, получаем c
. Возьмем такое число с > a, чтобы 1<c<b. Рассуждая, как и в случае 1, получаем c 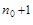
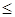 b
b 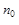 для некоторого n0
для некоторого n0 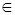 N. Тогда
N. Тогда 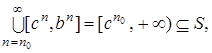 что также невозможно по лемме 4.
что также невозможно по лемме 4.
Докажем, что S нульмерно. Пусть V – произвольное открытое множество в S и 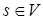 . Требуется показать, что существует такое открыто-замкнутое в S множество U, что
. Требуется показать, что существует такое открыто-замкнутое в S множество U, что  . Поскольку топология в S индуцируется топологией числовой прямой, то существуют такие числа a и b
. Поскольку топология в S индуцируется топологией числовой прямой, то существуют такие числа a и b 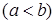 , что
, что 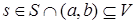 . Если
. Если 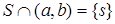 , то это и есть открыто-замкнутое множество U. Пусть левее s в интервале
, то это и есть открыто-замкнутое множество U. Пусть левее s в интервале  нет точек множества S, а правее – есть, и точка с - одна из них. По доказанному выше существует точка
нет точек множества S, а правее – есть, и точка с - одна из них. По доказанному выше существует точка 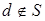 , такая, что
, такая, что 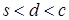 . В этом случае
. В этом случае 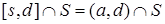 – искомое открыто-замкнутое множество U. Аналогично рассматривается случай, когда левее точки s в интервале
– искомое открыто-замкнутое множество U. Аналогично рассматривается случай, когда левее точки s в интервале 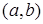 есть точки множества S, а правее нет, и случай, когда интервал
есть точки множества S, а правее нет, и случай, когда интервал 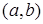 содержит точки из S и справа и слева от s. Предложение доказано.
содержит точки из S и справа и слева от s. Предложение доказано.
С помощью предложения 2 можно получить следующую топологическую классификацию числовых НОД-полугрупп.
Предложение 3. Любая НОД-полугруппа S относится к одному из следующих классов:
1. S связно.
2. S нульмерно, замкнуто в R + и 0 – предельная точка для S .
3. S нульмерно, не замкнуто в R + и 0 – предельная точка для S .
|
|
|
4. Точка 0 изолирована в S.
Доказательство. По лемме 1 существуют полугруппы 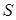 , которые являются связными множествами. Пусть
, которые являются связными множествами. Пусть 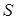 несвязно. Если
несвязно. Если 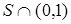 =Æ, то 0 – изолированная точка. Если существует элемент
=Æ, то 0 – изолированная точка. Если существует элемент 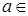
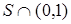 , то
, то 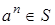 для любого
для любого 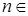 N и последовательность
N и последовательность  сходится к 0. Следовательно, 0 – предельная точка для S, множество
сходится к 0. Следовательно, 0 – предельная точка для S, множество 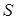 при этом может быть как замкнутым в R +, так и не замкнутым. Предложение доказано.
при этом может быть как замкнутым в R +, так и не замкнутым. Предложение доказано.
Дата добавления: 2019-07-15; просмотров: 157; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
