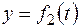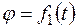Бумага офсетная. Офсетная печать. Усл.печ.л.3,19
КИНЕМАТИКА
Задача К1
Точка В движется в плоскости ху (рис. К1.0–К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями 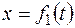 ,
,  , где х и у выражены в сантиметрах, t – в секундах.
, где х и у выражены в сантиметрах, t – в секундах.
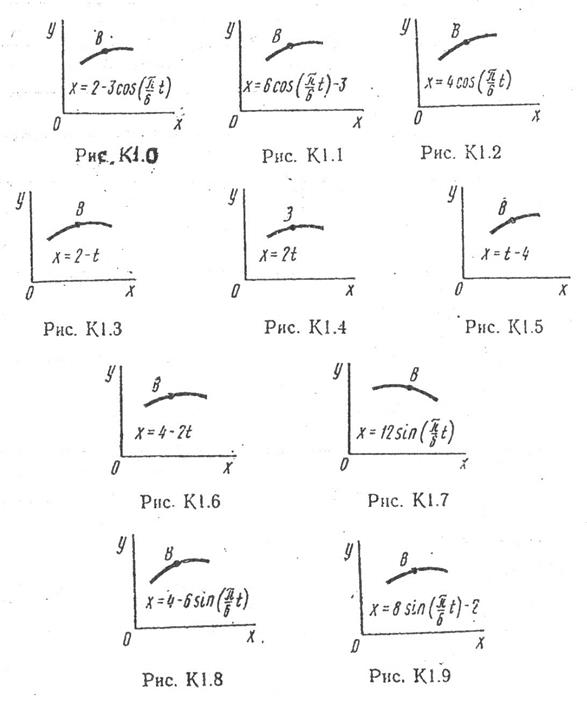
Таблица К1
| Номер условия |
| ||
| рис. 0 – 2 | рис. 3 – 6 | рис. 7 – 9 | |
| 0 | 
|

| 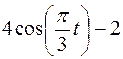
|
| 1 | 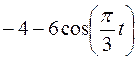
| 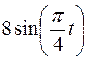
| 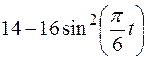
|
| 2 | 
|
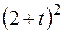
| 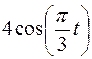
|
| 3 | 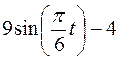
|
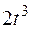
| 
|
| 4 | 
| 
| 
|
| 5 | 
|
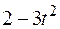
| 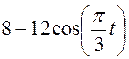
|
| 6 | 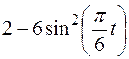
| 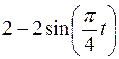
| 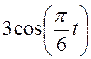
|
| 7 | 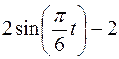
|
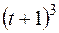
| 
|
| 8 | 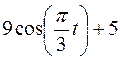
|

| 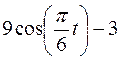
|
| 9 | 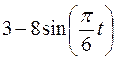
| 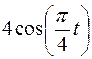
| 
|
Найти уравнение траектории точки; для момента времени t1 =1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость 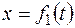 указана непосредственно на рисунках, а зависимость
указана непосредственно на рисунках, а зависимость  дана в табл. К1 (для рис. 0–2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7–9 в столбце 4). Как и в задачах С1–С5, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 – по последней.
дана в табл. К1 (для рис. 0–2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7–9 в столбце 4). Как и в задачах С1–С5, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 – по последней.
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорения точки.
В данной задаче все искомые величины нужно определить только для момента времени t1 =1 с. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы:
|
|
|
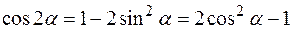 ;
; 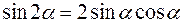 .
.
Пример К1. Даны уравнения движения точки в плоскости ху:
 ;
; 
(х, у – в сантиметрах, t – в секундах).
Определить уравнение траектории, построить траекторию, указать положение точки М на траектории в заданный момент времени t1 =1 с; для данного момента времени найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории; построить векторы скорости и указанных ускорений на рисунке.
Решение 1. Для определения уравнения траектории надо из заданных уравнений движения точки исключить время t. Поскольку время t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
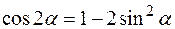 ,
, 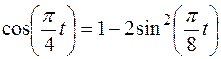 (1)
(1)
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим
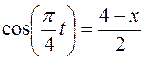 ,
, 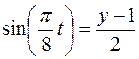 .
.
С учетом выражений (1) получаем
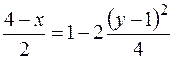 . (2)
. (2)
Отсюда окончательно получаем уравнение траектории точки М
 .
.
Следовательно точка М движется по параболе.
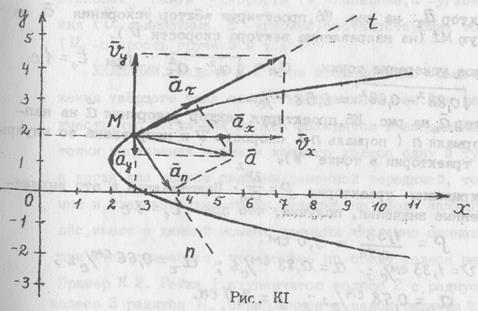
Строим параболу (2) на рис. К1.
|
|
|
 |
Находим координаты точки М в заданный момент времени t1 = =1 с.
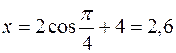 см;
см; 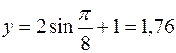 см.
см.
Указываем точку М (2,6; 1,76) на рис. К1.
2. Скорость точки найдем по её проекциям на оси координат:
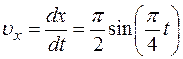 ;
; 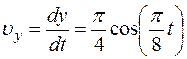 ;
;
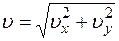 .
.
При t1 =1 с
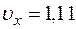 см/с,
см/с, 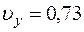 см/с,
см/с, 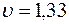 см/с (3)
см/с (3)
Вектор скорости 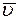 на рис. К1 строим по его проекциям. Вектор направлен по касательной к траектории в точке М.
на рис. К1 строим по его проекциям. Вектор направлен по касательной к траектории в точке М.
3. Аналогично найдем ускорение точки М:
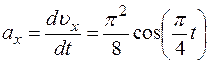 ;
; 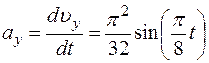 ;
;
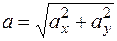 .
.
При t1 =1 с
 см/с2,
см/с2, 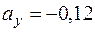 см/с2,
см/с2, 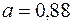 см/с2. (4)
см/с2. (4)
Вектор ускорения 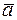 на рис. К1 строим по его проекциям. Вектор направлен в сторону вогнутости траектории в точке М.
на рис. К1 строим по его проекциям. Вектор направлен в сторону вогнутости траектории в точке М.
4. Касательное ускорение точки найдем, дифференцируя по времени равенство 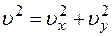 . Получим:
. Получим:
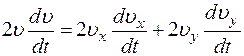 ; тогда
; тогда 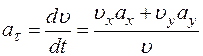 . (5)
. (5)
При t1 =1 с 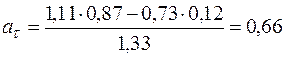 см/с2.
см/с2.
Строим вектор 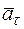 на рис. К1, проектируя вектор ускорения
на рис. К1, проектируя вектор ускорения 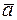 на касательную М t (на направление вектора скорости
на касательную М t (на направление вектора скорости 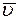 ).
).
5. Нормальное ускорение точки  . При t1 =1 с
. При t1 =1 с
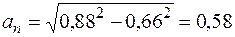 см/с2.
см/с2.
Строим вектор 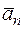 на рис. К1, проектируя вектор ускорения
на рис. К1, проектируя вектор ускорения 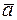 на направление нормали n (нормаль n
на направление нормали n (нормаль n 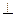 скорости
скорости 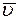 и направлена во внутрь вогнутости траектории в точке М).
и направлена во внутрь вогнутости траектории в точке М).
6. Радиус кривизны траектории 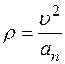 . Подставляем в это выражение ранее найденные значения, получим, что при t1 =1 с
. Подставляем в это выражение ранее найденные значения, получим, что при t1 =1 с
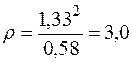 см.
см.
|
|
|
Ответ: 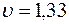 см/с,
см/с, 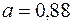 см/с2,
см/с2,  см/с2,
см/с2, 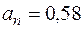 см/с2,
см/с2, 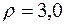 см.
см.
Задача К2
Механизм состоит из ступенчатых колес 1-3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес (рис. К2.0–К2.9, табл. К2). Радиусы ступеней колес равны соответственно: у колеса 1 – r1 =2 см, R1 = 4 см, у колеса 2 – r2 =6 см, R2 = 8 см, у колеса 3 – r3 =1 2 см, R3 = 16 см. На ободах колес расположены точки А, В, и С.
| Номер условия | Дано | Найти | |
| скорости | ускорения | ||
| 0 | 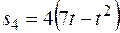
| 
| 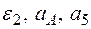
|
| 1 | 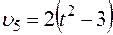
| 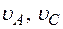
| 
|
| 2 | 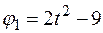
| 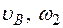
| 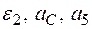
|
| 3 | 
| 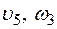
| 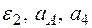
|
| 4 | 
| 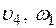
| 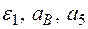
|
| 5 | 
| 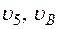
| 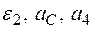
|
| 6 | 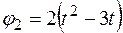
| 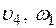
| 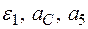
|
| 7 | 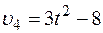
| 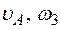
| 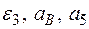
|
| 8 | 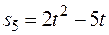
| 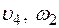
| 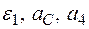
|
| 9 | 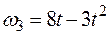
| 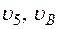
| 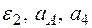
|
 |
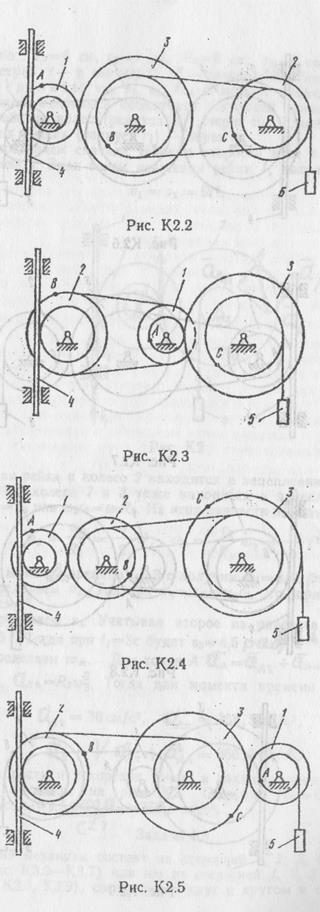
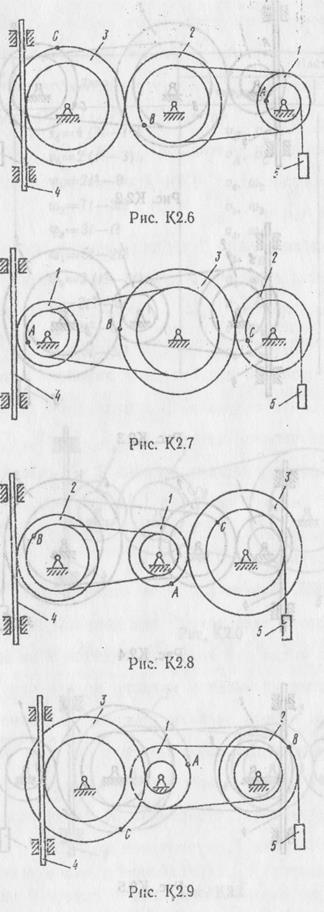
В столбце “Дано” таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где 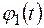 – закон вращения колеса 1,
– закон вращения колеса 1, 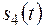 – закон движения рейки 4,
– закон движения рейки 4, 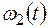 – закон изменения угловой скорости колеса 2,
– закон изменения угловой скорости колеса 2, 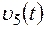 – закон изменения скорости груза 5 и т. д. (везде φ выражен в радианах, s – в сантиметрах, t – в секундах). Положительное направление для φ и ω против хода часовой стрелки, для
– закон изменения скорости груза 5 и т. д. (везде φ выражен в радианах, s – в сантиметрах, t – в секундах). Положительное направление для φ и ω против хода часовой стрелки, для 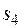 ,
, 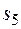 и
и 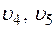 – вниз.
– вниз.
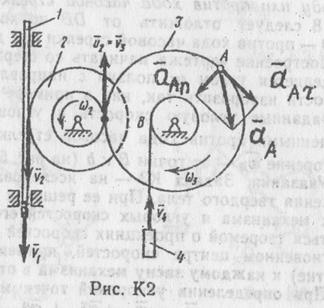
Определить в момент времени t1 = 2 с указанные в таблице в столбцах "Найти" скорости ( 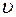 – линейные, ω – угловые) и ускорения (а – линейные, ε – угловые) соответствующих точек или тел (
– линейные, ω – угловые) и ускорения (а – линейные, ε – угловые) соответствующих точек или тел ( 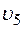 – скорость груза 5 и т. д.).
– скорость груза 5 и т. д.).
|
|
|
Указания. Задача К2 – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что когда два колеса находятся в зацеплении, скорость точки зацепления имеет у каждого колеса одну и ту же величину, а когда два колеса связаны ременной передачей, то все точки ремня и, следовательно, точки, лежащие на ободе каждого из этих колес, имеют в данный момент времени численно одинаковые скорости; при этом считается, что ремень по ободу колеса не скользит.
 |
Пример К2. Рейка 1, ступенчатое колесо 2 с радиусами
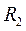 и
и  и колесо 3 радиуса
и колесо 3 радиуса 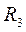 , скрепленное с валом радиуса
, скрепленное с валом радиуса 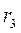 , находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К2). Рейка движется по закону
, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К2). Рейка движется по закону  .
.
Дано: R2 = 6 см, r2 = 4 см, R3 = 8 см, r3 = 3 см, 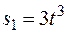 (s – в сантиметрах, t - в секундах), А – точка обода колеса 3, t1 = 3 с.
(s – в сантиметрах, t - в секундах), А – точка обода колеса 3, t1 = 3 с.
Определить: 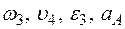 в момент времени t = t1.
в момент времени t = t1.
Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса  ), через
), через 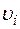 , а точек, лежащих на внутренних ободах (радиуса
, а точек, лежащих на внутренних ободах (радиуса 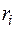 ), – через
), – через 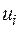 .
.
1. Определяем сначала угловые скорости всех колес, как функции времени t. Зная закон движения рейки 1, находим её скорость
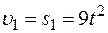 . (1)
. (1)
Так как рейка и колесо 2 находятся в зацеплении, то  или
или 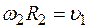 . Но колеса 2 и 3 тоже находятся в зацеплении, следовательно,
. Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, 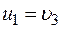 или
или 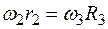 . Из этих равенств находим
. Из этих равенств находим
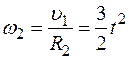 ,
,  . (2)
. (2)
Тогда для момента времени t1 = 3 с получим  рад/с.
рад/с.
3. Определяем 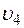 . Так как
. Так как 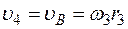 , то при t1 = 3 с будет
, то при t1 = 3 с будет 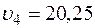 см/с2.
см/с2.
4. Определяем 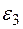 . Учитывая второе из равенств (2), получим
. Учитывая второе из равенств (2), получим 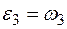 . Тогда при t1 = 3 с будет
. Тогда при t1 = 3 с будет 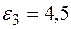 рад/с2.
рад/с2.
5. Определяем 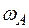 . Для точки А
. Для точки А 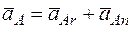 , где численно
, где численно 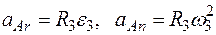 . Тогда для момента времени t1 = 3 с будем иметь:
. Тогда для момента времени t1 = 3 с будем иметь:
 см/с2,
см/с2, 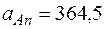 см/с2,
см/с2,
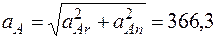 см/с2.
см/с2.
Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис. К2.
Ответ:  рад/с,
рад/с, 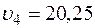 см/с2;
см/с2; 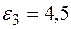 рад/с2,
рад/с2,  см/с2.
см/с2.
Задача К3
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В или Е (рис. К3.0-К3.7) или же из стержней 1, 2, 3 и ползунов В и Е (рис. К3.8, К3.9), соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами; точка O находится в середине стержня АВ. Длины стержней равны соответственно: l1= 0,4 м, l2 =1,2 м, l3 =1,4 м, l4=0,6 м. Положение механизма определяется углами α, β, γ, φ, θ. Значения этих углов и других заданных величин указаны в табл. К3а (для рис. 0 – 4) или в табл. К3б (для рис. 5 – 9); при этом в табл. К3а ω1 и ω2 – величины постоянные.
Определить величины, указанные в таблицах в столбцах "Найти".
Таблица К3а (к рис. К3.0–К3.4)
| Номер условия | Углы | Дано | Найти | ||||||||
| α° | β° | γ° | φ° | θ° | ω1,

| ω2,

| 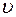 точек
точек
| ω звена | а точки | ε звена | |
| 0 1 2 3 4 5 6 7 8 9 | 0 90 30 60 30 90 90 0 60 30 | 60 120 60 150 30 120 150 60 150 120 | 30 150 30 150 60 120 120 60 120 150 | 0 0 0 90 0 90 90 0 90 0 | 120 30 120 30 150 60 30 120 30 60 | 6 - 5 - 4 - 3 - 2 - | - 4 - 5 - 6 - 2 - 8 | В, Е А, Е В, Е А, Е D, Е А, Е В, Е А, Е D, Е А, Е | D Е АВ АВ D Е АВ АВ D Е D Е АВ D Е | В А В А В А В А В А | АВ АВ АВ АВ АВ АВ АВ АВ АВ АВ |
Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол γ на рис. 8 следует отложить от DB по ходу часовой стрелки, а на рис. 9– против хода часовой стрелки и т. д.).


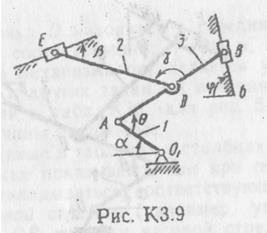
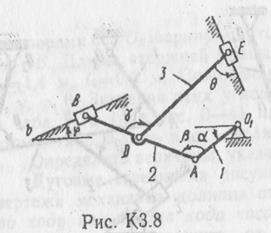
Таблица К3б (к рис. К3.5–К3.9)
| Номер условия | Углы | Дано | Найти | ||||||||||
| α° | β° | γ° | φ° | θ° | ω1,
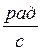
| ε1,

| 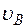 ,
м/с ,
м/с
| аВ, м/с2 | 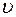 точек
точек
| ω звена | а точки | ε звена | |
| 0 1 2 3 4 5 6 7 8 9 | 120 0 60 0 30 90 0 30 90 60 | 30 60 150 150 120 120 150 120 120 60 | 30 90 30 30 120 90 90 30 120 60 | 90 0 90 0 0 90 0 0 90 90 | 150 120 30 60 60 60 120 60 150 30 | 2 - 3 - 4 - 5 - 6 - | 4 - 5 - 6 - 8 - 10 - | - 4 - 6 - 8 - 2 - 5 | - 6 - 8 - 10 - 5 - 4 | В, Е А, Е В, Е А, Е В, Е D, Е В, Е А, Е В, Е D, Е | АВ D Е АВ АВ D Е D Е D Е АВ D Е АВ | В А В А В А В А В А | АВ АВ АВ АВ АВ АВ АВ АВ АВ АВ |
Построение чертежа начинать со стержня, направление которого определяется углом α; ползун с направляющими для большей наглядности изобразить так, как в примере К3 (см. рис. К3б).
Заданные угловую скорость и угловое ускорение считать направленными против хода часовой стрелки, а заданные скорость 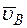 и ускорение
и ускорение 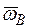 – от точки B к b (на рис. 5–9).
– от точки B к b (на рис. 5–9).
Указания. Задача К3 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
При определении; ускорений точек механизма исходить из векторного равенства 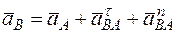 , где А – точка, ускорение
, где А – точка, ускорение 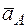 которой или задано или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то
которой или задано или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то 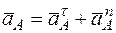 ); В – точка, ускорение
); В – точка, ускорение 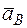 в которой нужно определить (если точка В движется по дуге окружности радиуса l, то
в которой нужно определить (если точка В движется по дуге окружности радиуса l, то 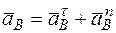 , где численно
, где численно 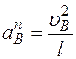 ; входящая сюда скорость
; входящая сюда скорость 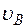 определяется так же, как и скорости других точек механизма).
определяется так же, как и скорости других точек механизма).
Пример К3. Механизм (рис. К3а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами.

Дано: α = 60°, β = 150°, γ = 90°, φ = 30°, θ =30°, А D = D В, l1=0,4 м, l2 =1,2 м, l3 =1,4 м, ω1 = 2 рад/с, ε1 = 7 рад/с2 (направления ω1 и ε1 – против хода часовой стрелки).
Определить:  .
.
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. К3б).
2. Определяем 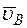 . Точка В принадлежит стержню АВ. Чтобы найти
. Точка В принадлежит стержню АВ. Чтобы найти  , надо знать скорость какой-нибудь другой точки этого стержня п направление
, надо знать скорость какой-нибудь другой точки этого стержня п направление 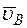 . По данным задачи, учитывая направление ω1 можем определить
. По данным задачи, учитывая направление ω1 можем определить  ; численно
; численно
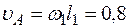 м/с;
м/с; 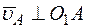 . (1)
. (1)
Направление 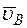 найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная
найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная 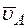 и направление
и направление 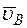 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 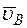 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
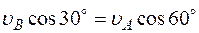 и
и 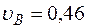 м/с. (2)
м/с. (2)
3. Определяем 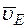 . Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить
. Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить 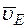 , надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная
, надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная  и
и 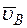 , строим мгновенный центр скоростей (МЦС) стержня АВ; это точка
, строим мгновенный центр скоростей (МЦС) стержня АВ; это точка  , лежащая на пересечении перпендикуляров к
, лежащая на пересечении перпендикуляров к  и ,
и , 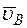 восставленных из точек А и В (к
восставленных из точек А и В (к  перпендикулярен стержень 1). По направлению вектора
перпендикулярен стержень 1). По направлению вектора  определяем направление поворота стержня АВ вокруг МЦС
определяем направление поворота стержня АВ вокруг МЦС 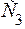 . Вектор
. Вектор  будет перпендикулярен отрезку C3D, соединяющему точки D и
будет перпендикулярен отрезку C3D, соединяющему точки D и 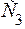 , и направлен в сторону поворота. Величину
, и направлен в сторону поворота. Величину  найдем из пропорции
найдем из пропорции
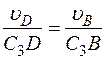 . (3)
. (3)
Чтобы вычислить C3D и С3В, заметим, что  прямоугольный, так как острые углы в нем равны 30
прямоугольный, так как острые углы в нем равны 30  и 60°, и что С3В=АВsin30°= = 0,5AB = BD. Тогда
и 60°, и что С3В=АВsin30°= = 0,5AB = BD. Тогда 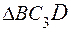 является равносторонним и C3B = C3D. В результате равенство (3) дает
является равносторонним и C3B = C3D. В результате равенство (3) дает
 м/с;
м/с; 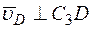 . (4)
. (4)
Так как точка Е принадлежит одновременно стержню 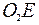 , вращающемуся вокруг О2, то
, вращающемуся вокруг О2, то 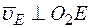 . Тогда восставляя из точек Е и О перпендикуляры к скоростям
. Тогда восставляя из точек Е и О перпендикуляры к скоростям 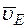 и
и  , построим МЦС С2 стержня DE. По направлению вектора
, построим МЦС С2 стержня DE. По направлению вектора  определяем направление поворота стержня DE вокруг центра С2. Вектор
определяем направление поворота стержня DE вокруг центра С2. Вектор 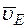 будет направлен в сторону поворота этого стержня. Из рис. К3б видно, что
будет направлен в сторону поворота этого стержня. Из рис. К3б видно, что  =
=  , откуда
, откуда 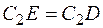 . Составив теперь пропорцию, найдем, что
. Составив теперь пропорцию, найдем, что
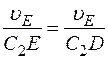 ,
, 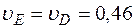 м/с. (5)
м/с. (5)
4. Определяем ω2. Так как МЦС стержня 2 нам известен (точка C2) и
 м, то
м, то  рад/с. (6)
рад/с. (6)
5. Определяем 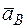 Точка В принадлежит стержню АВ. Чтобы найти
Точка В принадлежит стержню АВ. Чтобы найти 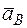 , надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить
, надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить 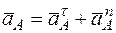 , где численно
, где численно
 м/с2;
м/с2; 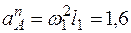 м/с2. (7)
м/с2. (7)
Вектор 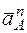 направлен вдоль AO1, а
направлен вдоль AO1, а 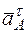 – перпендикулярно AO1; изображаем эти векторы на чертеже.
– перпендикулярно AO1; изображаем эти векторы на чертеже.
Так как точка В одновременно принадлежит ползуну, то вектор  будет параллелен направляющим ползуна. Изображаем вектор
будет параллелен направляющим ползуна. Изображаем вектор  на чертеже, полагая, что он направлен в ту же сторону, что и
на чертеже, полагая, что он направлен в ту же сторону, что и 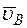
Для определения  воспользуемся равенством
воспользуемся равенством
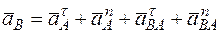 . (8)
. (8)
Изображаем на чертеже векторы 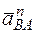 (вдоль ВА от В к А) и
(вдоль ВА от В к А) и 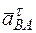 (в любую сторону перпендикулярно ВА); численно
(в любую сторону перпендикулярно ВА); численно 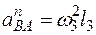 . Найдя ω3 с помощью построенного ранее МЦС C3 стержня 3, получим
. Найдя ω3 с помощью построенного ранее МЦС C3 стержня 3, получим
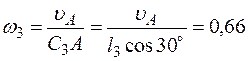 рад/с, и
рад/с, и 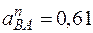 м/с2. (9)
м/с2. (9)
Таким образом, у величин, входящих в равенство (3), неизвестны только численные значения 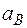 и
и 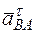 ; их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.
; их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.
Чтобы определить 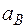 , спроектируем обе части равенства (8) на направление АВ (ось x), перпендикулярное к неизвестному вектору
, спроектируем обе части равенства (8) на направление АВ (ось x), перпендикулярное к неизвестному вектору 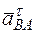 . Тогда получим
. Тогда получим
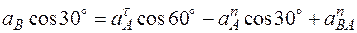 . (10)
. (10)
Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что
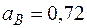 м/с2. (11)
м/с2. (11)
Так как получилось 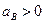 , то, следовательно, вектор
, то, следовательно, вектор  имеет направление, показанное на рис. К3б.
имеет направление, показанное на рис. К3б.
6. Определяем 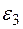 . Чтобы найти
. Чтобы найти 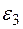 , сначала определим
, сначала определим 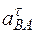 . Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось y). Тогда получим
. Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось y). Тогда получим
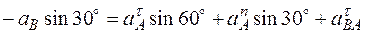 . (12)
. (12)
Подставив в равенство (12) числовые значения всех величин из (11) и (7), найдем, что  м/с2 указывает, что направление
м/с2 указывает, что направление 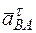 противоположно показанному на рис. К3б. Теперь из равенства
противоположно показанному на рис. К3б. Теперь из равенства  получим
получим
 рад/с2.
рад/с2.
Ответ: 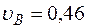 м/с,
м/с, 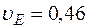 м/с,
м/с, 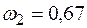 рад/с,
рад/с,  м/с2,
м/с2,  рад/с2.
рад/с2.
Задача К4
Прямоугольная пластина (рис. К4.0–К4.4) или круглая пластина радиуса R = 60 см (рис. К4.5–К4.9) вращается вокруг неподвижной оси по закону  , заданному в табл. К4. Положительное направление отсчета угла
, заданному в табл. К4. Положительное направление отсчета угла 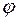 показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку O (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения OO1, лежит в плоскости пластины (пластика вращается в пространстве).
показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку O (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения OO1, лежит в плоскости пластины (пластика вращается в пространстве).
Таблица К4
| Номер условия | Для всех рисунков
| Для рис. 0–4 | Для рис. 5–9 | ||
| а, см |
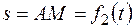
| h |

| ||
| 0 | 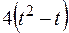
| 12 | 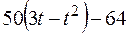
| R | 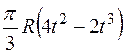
|
| 1 | 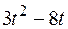
| 16 | 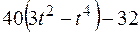
| 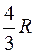
| 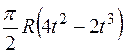
|
| 2 | 
| 10 | 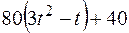
| R | 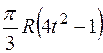
|
| 3 | 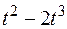
| 16 | 
| R | 
|
| 4 | 
| 8 | 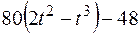
| R | 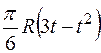
|
| 5 | 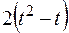
| 20 | 
| R | 
|
| 6 | 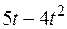
| 12 | 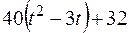
| 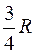
| 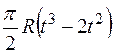
|
| 7 | 
| 8 | 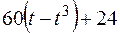
| R | 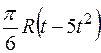
|
| 8 | 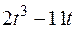
| 10 | 
| R | 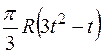
|
| 9 | 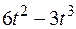
| 20 | 
| 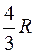
| 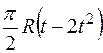
|
По пластине вдоль прямой BD (рис. 0–4) или по окружности радиуса R (рис. 5–9) движется точка М; закон ее относительного движения, т. е. зависимость 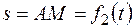 (s выражено в сантиметрах, t – в секундах), задан в таблице отдельно для рис. 0–4 и для рис. 5–9; там же даны размеры а и h. На рисунках точка M показана в положении, при котором
(s выражено в сантиметрах, t – в секундах), задан в таблице отдельно для рис. 0–4 и для рис. 5–9; там же даны размеры а и h. На рисунках точка M показана в положении, при котором 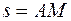 >0 (при s < 0 точка М находится по другую сторону от точки А).
>0 (при s < 0 точка М находится по другую сторону от точки А).

Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 с.
Указания. Задача К4 - на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка М на пластине в момент времени t1 = 1 с, и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче).
В случаях, относящихся к рис. 5–9, при решении задачи не подставлять числового значения R, пока не будут определены положение точки М в момент времени t1 = 1 с и угол между радиусами СМ и СА в этот момент.
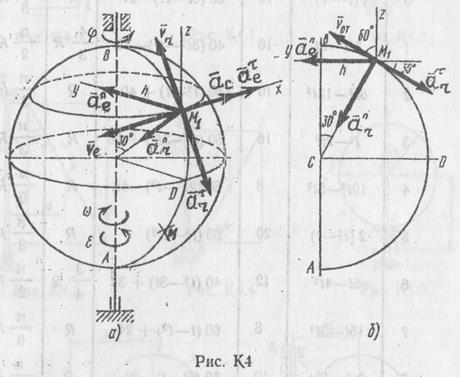
Пример К4. Шар радиуса R (рис. К4, а) вращается вокруг своего диаметра АВ по закону  (положительное направление отсчета угла
(положительное направление отсчета угла 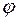 показано на рис. К4, а дуговой стрелкой). По дуге большого круга («меридиану») ADB движется точка М по закону
показано на рис. К4, а дуговой стрелкой). По дуге большого круга («меридиану») ADB движется точка М по закону 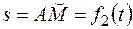 ; положительное направление отсчета расстояния s от A к D.
; положительное направление отсчета расстояния s от A к D.
Дано: 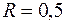 м,
м,  ,
, 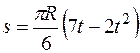 (
( 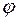 – в радианах, s – в метрах, t – в секундах).
– в радианах, s – в метрах, t – в секундах).
Определить:  и
и 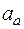 в момент времени t1 = 1 с.
в момент времени t1 = 1 с.
Решение. Рассмотрим движение точки М как сложное, считая ее движение по дуге  относительным (
относительным ( 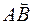 – относительная траектория точки), а вращение шара – переносным движением. Тогда абсолютная скорость
– относительная траектория точки), а вращение шара – переносным движением. Тогда абсолютная скорость 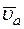 , и абсолютное ускорение
, и абсолютное ускорение 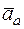 точки найдутся по формулам:
точки найдутся по формулам:
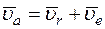 ,
, 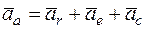 , (1)
, (1)
где в свою очередь, 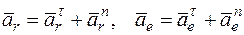 .
.
Определим все характеристики относительного и переносного движений.
1.Относительное движение. Это движение происходит по закону
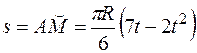 . (2)
. (2)
Сначала установим, где будет находиться точка М на дуге 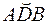 в момент времени t1. Полагая в уравнении (2) t1 = 1 с, получим
в момент времени t1. Полагая в уравнении (2) t1 = 1 с, получим 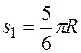
Тогда  или
или 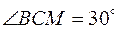 . Изображаем на рис. К4, а точку в положении, определяемом этим углом (точка М1).
. Изображаем на рис. К4, а точку в положении, определяемом этим углом (точка М1).
Теперь находим числовые значения 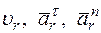 :
:
 ,
, 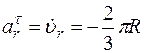 ,
,  ,
,
где 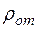 – радиус кривизны относительной траектории, то есть дуги
– радиус кривизны относительной траектории, то есть дуги 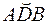 . Для момента времени t1 = 1 с, учитывая, что
. Для момента времени t1 = 1 с, учитывая, что  , получим:
, получим:
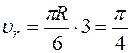 м/с,
м/с, 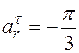 м/с2,
м/с2, 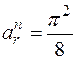 м/с2. (3)
м/с2. (3)
Знаки показывают, что вектор 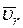 направлен в сторону положительного отсчета расстояния s, а вектор
направлен в сторону положительного отсчета расстояния s, а вектор  – в противоположную сторону; вектор
– в противоположную сторону; вектор 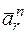 направлен к центру С дуги
направлен к центру С дуги 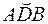 . Изображаем все эти векторы на рис. К4, а. Для наглядности приведен рис. К4, б, где дуга
. Изображаем все эти векторы на рис. К4, а. Для наглядности приведен рис. К4, б, где дуга 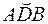 совмещена с плоскостью чертежа.
совмещена с плоскостью чертежа.
2. Переносное движение. Это движение (вращение) происходит по закону 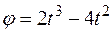 . Найдем угловую скорость ω и угловое ускорение
. Найдем угловую скорость ω и угловое ускорение  переносного вращения:
переносного вращения:  ,
, 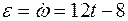 и при t1 = 1 с
и при t1 = 1 с
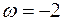 рад/с,
рад/с,  рад/с2. (4)
рад/с2. (4)
Знаки указывают, что при t1 = 1 с направление  совпадает с направлением положительного отсчета угла
совпадает с направлением положительного отсчета угла 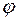 , а направление ω ему противоположно; отметим это на рис. К4, а соответствующими дуговыми стрелками.
, а направление ω ему противоположно; отметим это на рис. К4, а соответствующими дуговыми стрелками.
Для определения  и
и 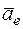 находим сначала расстояния h точки М1 от оси вращения. Получаем
находим сначала расстояния h точки М1 от оси вращения. Получаем  м. Тогда в момент времени t1 = 1 с, учитывая равенства (4), будем иметь:
м. Тогда в момент времени t1 = 1 с, учитывая равенства (4), будем иметь:
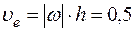 м/с,
м/с, 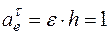 м/с2,
м/с2,
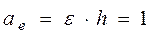 м/с2. (5)
м/с2. (5)
Изображаем на рис. К4, а векторы  и
и 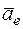 с учетом направлений ω и
с учетом направлений ω и  и вектор
и вектор 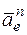 (направлен к оси вращения).
(направлен к оси вращения).
3. Кориолисово ускорение. Так как угол между векторами 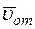 и осью вращения (вектором
и осью вращения (вектором 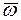 ) равен 60°, то численно в момент времени t1 = 1 с [см. равенства (3) и (4)]
) равен 60°, то численно в момент времени t1 = 1 с [см. равенства (3) и (4)]
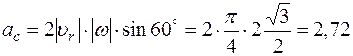 м/с2. (6)
м/с2. (6)
Направление  найдем, спроектировав вектор
найдем, спроектировав вектор 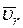 на плоскость, перпендикулярную оси вращения (проекция направлена так же, как вектор
на плоскость, перпендикулярную оси вращения (проекция направлена так же, как вектор 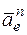 ), и повернув затем эту проекцию в сторону ω, то есть по ходу часовой стрелки, на 90°. Иначе направление
), и повернув затем эту проекцию в сторону ω, то есть по ходу часовой стрелки, на 90°. Иначе направление  можно найти, учтя, что
можно найти, учтя, что  . Изображаем вектор
. Изображаем вектор  на рис. К4а.
на рис. К4а.
Теперь можно вычислить значения 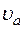 и
и  .
.
4. Определение 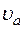 . Так как
. Так как  , а векторы
, а векторы  и
и 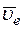 взаимно перпендикулярны (см. рис. К4а), то в момент времени t1 = 1 с
взаимно перпендикулярны (см. рис. К4а), то в момент времени t1 = 1 с
 м/с.
м/с.
5. Определение 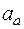 . Вектор
. Вектор  слагается из следующих векторов:
слагается из следующих векторов: 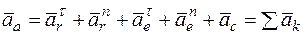 . Для определения
. Для определения 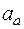 проведем координатные оси М1ху z (см. рис. К4а) и вычислим проекции вектора
проведем координатные оси М1ху z (см. рис. К4а) и вычислим проекции вектора  на эти оси. Учтем при этом, что векторы
на эти оси. Учтем при этом, что векторы  и
и  лежат на проведенной оси х, а векторы
лежат на проведенной оси х, а векторы  расположены в плоскости дуги
расположены в плоскости дуги 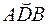 , то есть в плоскости М1у z (см. рис. К4б). Тогда для момента времени t1 = 1 с, учтя равенства (3), (5), (6), получим:
, то есть в плоскости М1у z (см. рис. К4б). Тогда для момента времени t1 = 1 с, учтя равенства (3), (5), (6), получим:
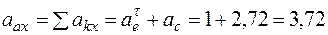 м/с2,
м/с2,
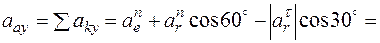
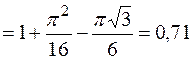 м/с2,
м/с2,
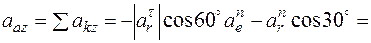
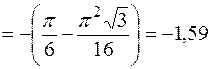 м/с2.
м/с2.
Отсюда находим значение 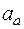 в момент времени t1 = 1 с:
в момент времени t1 = 1 с:
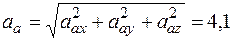 м/с2.
м/с2.
Ответ: 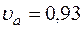 м/с,
м/с,  м/с2.
м/с2.
Теоретическая механика. Методические указания и контрольные задания по статике и кинематике для студентов-заочников машиностроительных специальностей
БУДНИК Ф е л и к с Г р и г о р ь е в и ч
Научный редактор Е.И. Селенский
Редактор издательства Л.Н. Мажугина
Компьютерный набор С.М. Васейкина
Иллюстрации С.М. Васейкина
Темплан 1999 г, п. 55
Подписано в печать от 20.04.99 г. Формат 60´84 1/16
Бумага офсетная. Офсетная печать. Усл.печ.л.3,19
Дата добавления: 2019-03-09; просмотров: 154; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!