Задания к практической работе 39
ПРАКТИЧЕСКАЯ РАБОТА 38
Выпуклость графика функции, точки перегиба
Цель: отработать навыки исследования графика функции на выпуклость и вогнутость с помощью производной, систематизация знаний по теме.
Краткое изложение теоретических вопросов:
График функции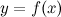 
, дифференцируемой на интервале 
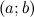, является на этом интервале выпуклым, если график этой функции в пределах интервала 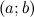лежит не выше любой своей касательной (рис. 1).
График функции 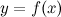, дифференцируемой на интервале 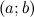, является на этом интервале вогнутым, если график этой функции в пределах интервала 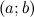лежит не ниже любой своей касательной (рис. 2).
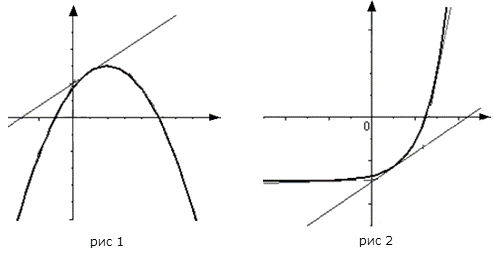
Схема исследования функции на выпуклость, вогнутость:
1. Находим вторую производную функции (это производная от первой производной).
2. Находим точки, в которых вторая производная равна нулю или не существует.
3. Исследуем знаки второй производной справа и слева от найденных точек.
Задание:
Исследуем на выпуклость, вогнутость функцию 
1. Найдем первую производную функции :
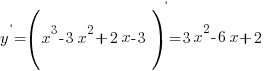
2. Найдем вторую производную функции .
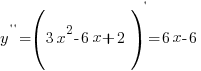
3. Найдем нули второй производной:
- точка перегиба.
Найдем знаки второй производной и определим промежутки выпуклости, вогнутости функции:
График нашей функции выглядит так:
Мы видим, что слева от точки функция выпуклая
Справа от точки функция вогнутая.
Задание.
Найти интервалы выпуклости/вогнутости функции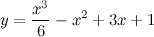 
|
|
|
Решение.
Найдем вторую производную заданной функции:
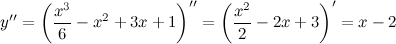
Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение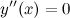 
:
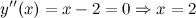
Исследуем знак второй производной слева и справа от полученной точки:
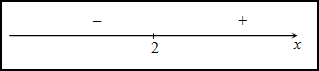
Так как на промежутке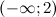 
вторая производная 
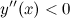, то на этом промежутке функция 
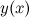выпукла; в силу того, что на промежутке 
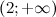вторая производная 
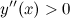- функция вогнута.
Так как при переходе через точку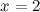 
вторая производная сменила знак, то эта точка является точкой перегиба графика функции.
Ответ. Точка 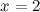- точка перегиба графика функции.
На промежутке 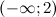функция выпукла, на промежутке 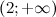функция вогнута.
ПРАКТИЧЕСКАЯ РАБОТА 39
Исследование функции
Цель: отработать навыки исследования графика функции с помощью производной, систематизация знаний по теме.
Краткое изложение теоретических вопросов:
Алгоритм исследования функции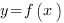 
:
1.Находим область определения функции .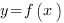
2. Если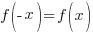 
, то функция четная. График четной функции симметричен относительно оси OY.
Если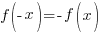 
, то функция нечетная. График нечетной функции симметричен относительно начала координат.
3.Находим точки пересечения графика с осями координат.
|
|
|
Находим нули функции - это точки пересечения графика функции 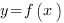с осью абсцисс (OX).
Для этого мы решаем уравнение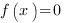 
.
Находим точку пересечения графика функции 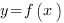с осью ординат (OY). Для этого ищем значение функции при 
.
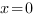4.Находим асимптоты графика функции.
5. Исследуем функцию с помощью производной: находим промежутки возрастания и убывания функции, а также точки максимума и минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную 
б) Приравниваем производную к нулю и находим корни уравнения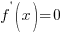 
- это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которых производная положительна, являются промежутками возрастания функции.
Промежутки, на которых производная отрицательна, являются промежутками убывания функции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
6. Находим точки перегиба и промежутки выпуклости и вогнутости.
Задание.
Исследуйте функцию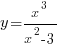 
и постройте ее график.
Решение.
1. Найдем область определения функции.
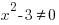
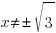
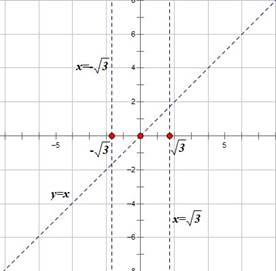
При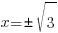 
знаменатель дроби равен нулю, следовательно, прямые 
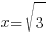и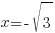 
являются вертикальными асимптотами графика функции .
|
|
|
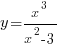2. Исследуем функцию на четность.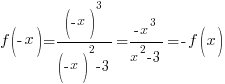 
Получили, что 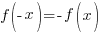, следовательно, функция 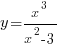- нечетная, и график функции симметричен относительно начала координат.
3. Найдем точки пересечения с осями координат.
а) Точки пересечения с осью ОХ (y=0)
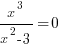
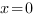
б) Точка пересечения с осью ОY (x=0)
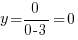
График нашей функции проходит через начало координат.
4. Найдем асимптоты графика функции .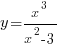
Вертикальные асимптоты мы уже нашли в п.1, это прямые 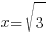и .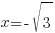
Уравнение горизонтальной асимптоты функции 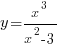имеет вид 
, где
.
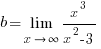Степень числителя дроби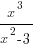 
на единицу больше степени знаменателя, поэтому 
не существует, и график функции 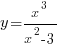не имеет горизонтальной асимптоты.
Попробуем найти наклонную асимптоту.
Уравнение наклонной асимптоты имеет вид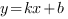 
.
Коэффициенты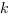 
и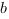 
вычисляются следующим образом:
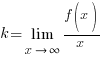
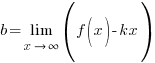
В нашем случае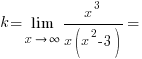 
.
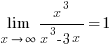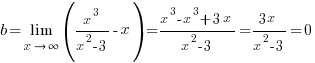(Степень знаменателя на единицу больше степени числителя).
То есть уравнение наклонной асимптоты имеет вид 
.
5. Найдем промежутки возрастания и убывания функции 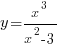и экстремумы.
а) Найдем производную функции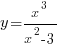
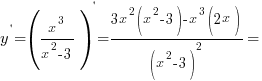
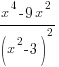
б) Приравняем производную к нулю: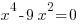 
; 
; 
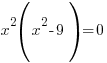
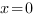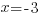в) Нанесем нули производной и корни ее знаменателя на числовую ось, расставим знаки и найдем точки экстремума и промежутки возрастания и убывания.
|
|
|
Найдем значение функции в точках экстремума:
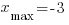
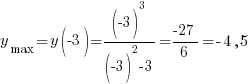
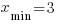
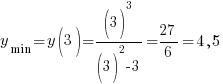
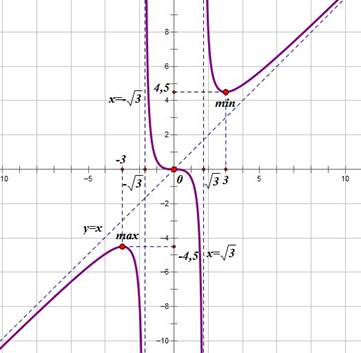
Задания к практической работе 39
Для указанной функции 
требуется провести полное исследование функции.
| 1 |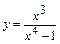 
| 
|
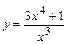
| 2 | 
| 
|
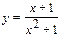
| 3 | 
| 
|
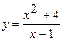
| 4 |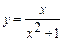 
| 
|
| 5 | 
| 
|
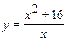
| 6 |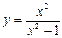 
| 
|
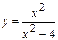
| 7 |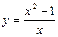 
| 
|
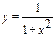
| 8 | 
| 
|
| 9 |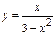 
| 
|
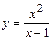
| 10 |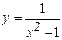 
| 
|
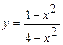
| 11 | 
| 
|
| 12 |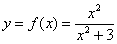 
| 
|
| 13 |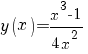 
| 
|
Дата добавления: 2019-03-09; просмотров: 170; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!