Геометрический смысл задачи линейного программирования
Решение задач линейного программирования
Лекция 3
Формы задач линейного программирования
Стандартная задача линейного программирования:
,
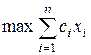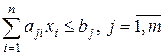, (1)
.
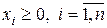Стандартная задача имеет важное значение ввиду того, что большое число прикладных моделей сводится именно к этому классу задач линейного программирования.
Каноническая задача линейного программирования:
,
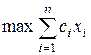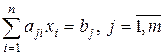, (2)
.
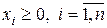Основные вычислительные методы (симплекс-метод и его модификации) решения задач линейного программирования разработаны именно для канонической задачи.
Общая задача линейного программирования:
,
,
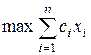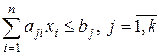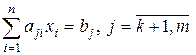, (3)
.
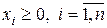Все три перечисленные задачи эквивалентны в том смысле, что каждую из них можно простыми преобразованиями привести к любой из двух остальных. Поэтому если есть способ решения одной из этих трех задач, то тем самым может быть решена и любая другая из двух остальных. Покажем, например, как можно привести стандартную задачу (1) к канонической форме (2). Для этого введем в рассмотрение новые переменные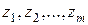 
, количество которых совпадает с числом ограничений в стандартной задаче, и рассмотрим следующую каноническую задачу:
,
,
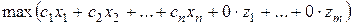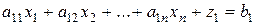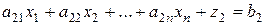, (4)
...
,
, 
, 
, 
.
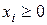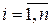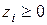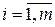Теорема. Пусть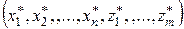 
решение сформулированной выше канонической задачи (4), полученной из стандартной задачи (1). Тогда решением исходной стандартной задачи (1) является вектор 
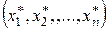. Без доказательства.
|
|
|
Рассмотреть другие варианты…
2.2. Система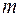 
линейных уравнений с 
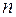переменными
Рассмотрим систему уравнений (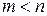 
):
,
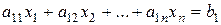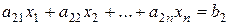, (5)
...
.
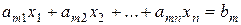Эта система может быть записана в виде: 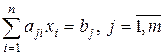или в матричном виде: 
.
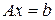В задачах линейного программирования рассматриваются системы, в которых ранг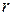 
матрицы 
, 
, 
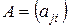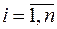меньше числа переменных, т.е.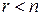 
. Это означает, что наибольшее число независимых переменных уравнений системы равно 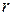. Далее будем полагать, что в системе (5) число независимых уравнений равно 
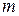, т.е. 
.
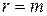Любые 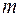переменных системы 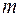линейных уравнений с 
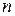неизвестными 
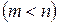называются основными, или базисными, если определитель матрицы коэффициентов при них не равен нулю. Тогда остальные 
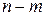переменных называются неосновными небазисными. Учитывая, что максимально возможное число сочетаний из 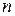элементов п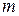о равно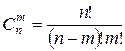 
, общее число комбинаций базисных переменных не превосходит 
.
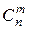Рассмотрим пример. Найти все возможные группы базисных переменных в системе
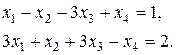
Общее число комбинаций базисных переменных не превосходит числа 
. Найти возможные комбинации базисных переменных! Выясним, например, являются ли базисными переменные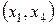 
.
|
|
|
Рассмотрим определитель из столбцов матрицы при переменных :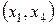
.
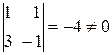Следовательно, переменные 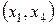являются базисными. Также можно выяснить, что базисными являются комбинации переменных 
, 
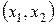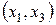. Комбинации 
, 
, 
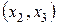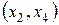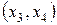не являются базисными.
Базисным решением системы линейных уравнений с переменными называются решения, в котором все 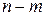неосновных переменных равны нулю.
В задачах линейного программирования особый интерес представляют допустимые базисные решения, или т.н. опорные планы.
Пример. Найти все базисные решения следующей системы:
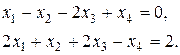
Легко установить, что существует три группы основных переменных 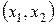, 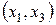. 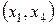, т.е. число базисных решений равно трем. Взяв за основные переменные 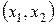, приравняв неосновные переменные к нулю, т.е. 
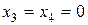, получим систему уравнений вида:
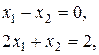
откуда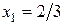 
, 
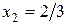, следовательно, первое базисное решение 
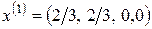допустимое. Если взять за основные переменные 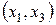и приравнять нулю остальные не основные переменные 
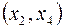, получим второе базисное решение 
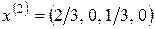. Аналогично, можно найти и третье базисное решение 
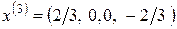, которое в силу отрицательности последней компоненты не является допустимым.
|
|
|
Геометрический смысл задачи линейного программирования
Рассмотрим следующую задачу линейного программирования:
, 
, 
.
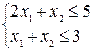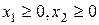Геометрическая интерпретация решения:
.
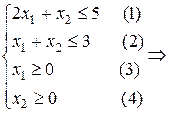
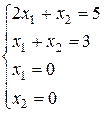Нормальное уравнение прямой: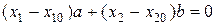 
,
,
,
.
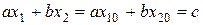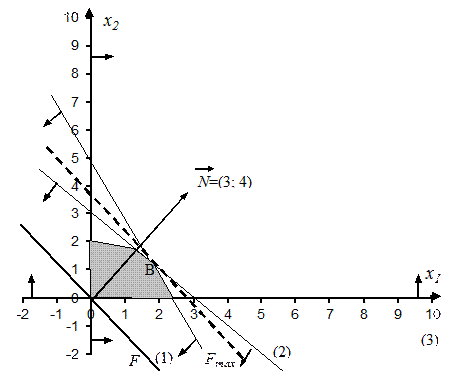
Рис. 1. Геометрическая интерпретация решения экстремальной задачи
То есть наискорейшее возрастание функции F будет в направлении вектора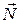 
. Координаты точки В удовлетворяют уравнению:
.
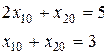
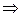
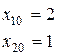
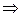
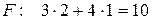Можно показать, что если задача линейного программирования имеет решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений системы ограничений. Поэтому для решения задачи линейного программирования необходимо перебрать конечное число базисных решений, выбрать среди них то, на котором целевая функция принимает экстремальное значение. Геометрически это соответствует перебору всех угловых (крайних) точек многогранника. Если оптимальное решение существует, то такой перебор приведет к нахождению оптимального решения. Однако такой прямой перебор связан с очень большим объемом вычислений. Число перебираемых допустимых базисных решений можно сократить, если производить перебор не произвольно, а добиваясь того, чтобы каждое последующее решение было бы не хуже предыдущего. Такой подход, хотя и не исключает теоретической возможности перебора всех угловых точек, на практике позволяет существенно сократить число шагов при отыскании экстремума. Поясним это на графическом примере (см. рис. 2).
|
|
|
Пусть область допустимых решений изображается многоугольником ABCDEFGH. Пусть угловая точка B соответствует исходному допустимому базисному решению. При произвольном переборе всех вершин мы могли бы исследовать все семь вершин многогранника. В то же время видно, что после точки B выгоднее перейти к точке C, а затем к точке D, которая и будет оптимальной, т.е. вместо семи точек перебрали только три.
Идея последовательного улучшения решения легла в основу симплексного метода, наиболее часто применяемого метода решения задач линейного программирования.
Рис. 2. Область допустимых решений
Геометрический смысл симплексного метода состоит в том, что осуществляется последовательный переход от одной вершины многогранника ограничений к другой, соседней, в которой линейная функция принимает значение не худшее, чем в предыдущей. Эта процедура продолжается до тех пор, пока не будет найдено оптимальное решение. Симплексный метод, позволяющий решать любую задачу линейного программирования, универсален. В настоящее время он используется в программном обеспечении для решения задач линейного программирования на компьютере. Для решения задач небольшой размерности он может использоваться вручную.
Симплексный метод состоит из трех основных элементов:
1) определения какого-либо первоначального допустимого базисного решения;
2) правила перехода к лучшему решению;
3) проверки оптимальности допустимого решения.
Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена не в виде неравенств, а в виде равенств.
Дата добавления: 2019-03-09; просмотров: 929; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!