Зависимость коэффициента гидравлического трения от режимов течения

ЛАБОРАТОРНАЯ РАБОТА № 1

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГО

 ТРЕНИЯ В СЛУЧАЕ ПОТЕРЬ ПО ДЛИНЕ

Задание:

Определить из опыта коэффициент гидравлического трения  при заданном расходе в имеющемся трубопроводе. Сравнить полученную экспериментальную величину коэффициента гидравлического трения  с вели­чиной теоретической , определяемой по справочным данным.

Теоретические основы метода:

Потери по длине

В механике жидкости и газа потери, возникающие в движущемся потоке жидкости разделяют на две большие группы: первая группа это потери связанные с трением по длине трубопровода, т.е. движущийся поток жидкости соприкасается со стенками трубопровода, в результате чего возникает сила трения между слоем жидкости ближе всего расположенном к стенке трубы и поверхностью самой трубы. Возникает данный вид потерь только в трубопроводах имеющих постоянное поперечное сечение при условии постоянной средней скорости по длине трубы. (вторая группа потерь будет рассматриваться в лабораторной №2).

Уравнение Бернулли

Для потока жидкости справедливо Уравнение Бернулли:

          

где 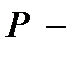 [Па] давление жидкости;

[кг/м³] плотность жидкости;

[м/с] средняя скорость потока жидкости;

Уравнение Бернулли можно переписать для двух выбранных сечений (см. рис. 1)

                                                                           (1)

где [м], геометрическая высота (геометрический напор) в соответствующем сечении;

[м], скоростная высота (скоростной напор) в соответствующем сечении;

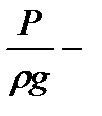[м], пьезометрическая высота (пьезометрический напор) в соответствующем сечении;

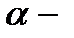коэффициент Кориолиса, учитывающий неравномерность распределения скоростей потока по поперечному сечению трубопровода;

[м], величина потерь напора на трение между сечениями 1-2 (см. рис. 1).

 

 

Описание лабораторного стенда

На рисунке 1 изображено: бак с жидкостью (1) из которого выходит два исследуемых трубопровода диаметры первого и второго трубопроводов 15 и 11 [мм], (3) с внутренней шероховатостью 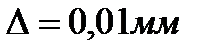. Шероховатость – совокупность неровностей поверхности. (на рисунке 1 изображён один условный трубопровод). 

В сечениях 1 и 2, расположены пьезометрические трубки (2) и (4), которые показывают величину пьезометрического напора . Разность между показаниями пьезометра (2) и показаниями пьезометра (4), отражает величину потерь напора на трение между сечениями 1 и 2.

Величина  и  - геометрическая высота, по сути, это расстояние от центра оси трубопровода до поверхности земли (в данном случае до поверхности пола аудитории).

В качестве жидкости применяется водопроводная вода, с плотностью 1000 [кг/м³], и кинематической вязкостью .

Рис. 1 Схематичное изображение лабораторного стенда

Допущения

В данной работе целесообразно принять следующие допущения:

эти расстояния равны между собой.

скорости в сечениях 1 и 2 равны друг другу, по причине постоянства расхода жидкости в трубопроводе;

коэффициенты Кориолиса равны друг другу и равны единице.

При применении вышеуказанных допущений, уравнение (1) будет выглядеть:

                                                                                                                             (2)

Таким образом, получаем формулу для определения, величины потерь напора на трение потока жидкости в трубопроводе при условии постоянства расхода.

 

Потери напора на трение

С другой стороны потери напора на трение определяются по формуле Дарси:

                                             ,                                                             (3)

где коэффициент гидравлического трения;

 длина трубопровода;

 диаметр трубопровода.

 Коэффициент гидравлического трения зависит от режима течения жидкости.

Режимы течения жидкости

В идеальном случае жидкость имеет два режима течения: ламинарный и турбулентный. В реальных трубопроводах имеет место три режима течения. Ламинарный – частицы жидкости движутся равномерно, слоисто, параллельно оси трубопровода. Турбулентный – частицы движутся хаотично, имеет место завихрения потока. Переходный – поток не имеет слоистую структуру, но и не имеет явно выраженного вихреобразования.

Определить режим течения жидкости можно по величине числа Рейнольдса:

,

где  кинематическая вязкость жидкости.

Для определения режима течение по числу Рейнольдса см. таблицу 1.

Таблица 1. Определение режима течения жидкости.

Режим течения	Число Рейнольдса
Ламинарный	Re <2320
Переходный	Re = 2320 - 4000
Турбулентный	Re >4000

 

Критическое значение числа Рейнольдса: . При достижении критического значения происходит смена режима течения жидкости.

Зависимость коэффициента гидравлического трения от режимов течения

---

Дата добавления: 2019-03-09; просмотров: 807; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!