ВЫБОР МЕТОДА РЕШЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

3.1. Анализ методов решения ОДУ

Для решения ОДУ существует множество методов. Одними из наиболее распространенных методов являются: метод Милна, Рунге-Кутта, Эйлера-Коши, разностный метод.

Рассмотрим сущность каждого метода решения ОДУ:

1.Метод Милна

Конечноразностный метод решения задачи Коши для системы обыкновенных дифференциальных уравнений первого порядка

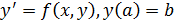(10)

В методе Милна используется конечноразностная формула

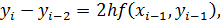(11)

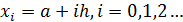(12)

Для вычисления по этой формуле необходимо каким-либо иным способом найти дополнительное начальное значение

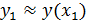(13)

Метод Милна имеет второй порядок точности, устойчив по Далквисту, т.е. все решения однородного разностного уравнения

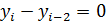(14)

ограничены равномерно по h при 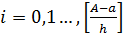для любого фиксированного значения отрезка [a , A]. Для устойчивости достаточно, чтобы простые корни характеристического многочлена левой части разностного уравнения не превосходили по модулю единицы, а кратные были по модулю строго меньше единицы. Многочлен 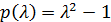имеет корни 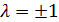и, следовательно, удовлетворяет указанному условию устойчивости. Однако при решении систем уравнений 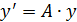с матрицей A, имеющей отрицательные собственные значения, происходит быстрый рост вычислительной погрешности.

2.Метод Рунге-Кутта

Формулы этого метода предназначены для интегрирования дифференциальных уравнений первого порядка вида

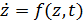(15)

с начальными условиями 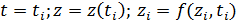(16)

Существуют формулы Рунге-Кутта, предназначенные для интегрирования дифференциального уравнения второго и третьего порядков, но они очень громоздки и на практике используются очень редко.

Методы Рунге-Кутта обладают следующими отличительными свойствами:

- они согласуются с методами Тейлора в плоть до членов порядка h^p, где степень р различна для различных методов и называется порядком метода.

- эти методы являются одноступенчатыми: чтобы найти y_m ₊₁, нужна информация о предыдущей точке x_m, y_m.

- они не требуют вычисления производных от f ( x , y ), а требуют только вычисления самой функции.

Именно благодаря третьему свойству методы Рунге-Кутта более удобны для практических вычислений. Однако для вычисления одной последующей точки решения приходится вычислять функцию f ( x , y ) несколько раз при различных значениях x и y. Этот метод требует большой квалификации и времени на отладки.

3.Метод Эйлера-Коши

Итерационный метод Эйлера-Коши применим для интегрирования дифференциальных уравнений любого порядка.

Если имеем дифференциальное уравнение

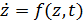, (17)

с начальными условиями 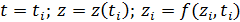(18)

то формула для интегрирования получается из следующих соображений.

Находят значения функции в виде трех членов разложения ряда Тейлора

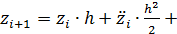… (19)

Затем вторая производная представляется в виде разностного выражения

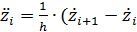) (20)

Подставив выражения (19) уравнение (18), получим:

(21)

В выражении (21) значение 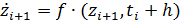неизвестно, поэтому, чтобы воспользоваться формулой (20), строятся итерационный процесс.

Таким образом, циклическая процедура вычислений по формуле (20) представляет итерационный метод Эйлера-Коши для дифференциального уравнения.

4.Разностный метод

Этот метод основан на замене производной в дифференциальных уравнениях их приближенными разностными аналогами.

В итоге система дифференциальных уравнений преобразуется к системе алгебраических уравнений. Алгоритм решения задачи прост, а программа машинной реализации требует минимума времени при отладке. Однако разностный метод является неустойчивым, то есть решение зависит от величины шага интегрирования. На практике вначале производят расчеты с целью определения шага интегрирования. Критерием выбора является условие, когда разность значений двух решений не превышает 5%.

Так как разностный метод прост в понимании физической сущности процесса и имеет короткий листинг программы, то в качестве метода решения полученной математической модели будем использовать его.

3.2. Описание алгоритма выбранного метода решения обыкновенных дифференциальных уравнений

Для интегрирования полученного обыкновенного дифференциального уравнения колебания кузова вагона на рессорах был выбран разностный метод интегрирования.

Рассмотрим произвольный график функции f=q(t) представленный на рисунке 7, где q – перемещение центра масс твердого тела, t – время, h – шаг разностной аппроксимации по времени.

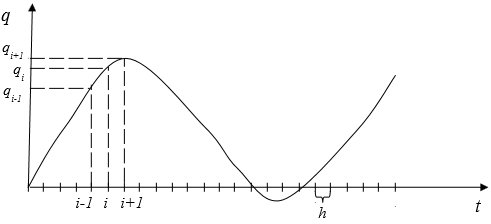
Рисунок 7 –Построение разностных аналогов

Алгоритм решения разностным методом заключается в следующем:

- определяем разностный аналог первой производной по формуле (22):

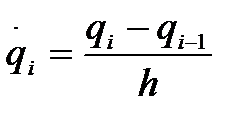, (22)

где 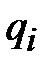– перемещение при текущем (i) значении времени;

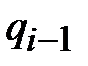– перемещение при предыдущем (i-1) значении времени;

h – шаг интегрирования или шаг разностной аппроксимации по времени.

Определяем разностный аналог второй производной по формуле 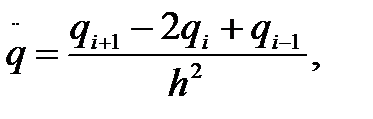(23):

(23)

где 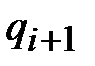– перемещение при последующем (i+1) значении времени;

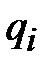– перемещение при текущем значении времени;

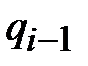– перемещение при предыдущем значении времени;

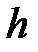– шаг интегрирования или шаг разностной аппроксимации по времени.

После вычисления разностных аналогов, заменим все производные в уравнении движения полученными разностными аналогами (24):

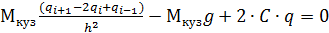, (24)

Выражаем из уравнения (24) значение 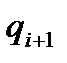и получаем следующие уравнения:

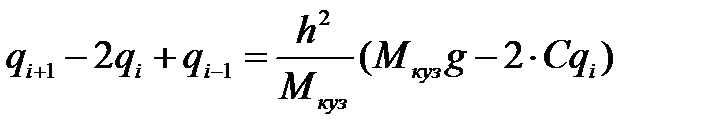, (25)

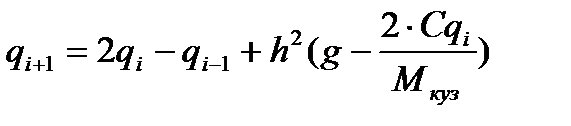, (26)

Выражения (25) и (26) являются уравнениями движения, в разностной форме, представляющее собой систему линейных алгебраических уравнений.

В этом случае математическая модель будет иметь вид – система (20):

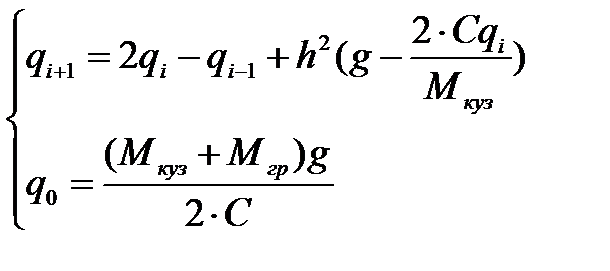, (27)

Таким образом, совершили переход от системы обыкновенных дифференциальных уравнений к системе алгебраических уравнений. Получили математическую модель собственных колебаний вагона на рессорном подвешивании в разностном виде.

Определим шаг аппроксимации h для задачи:

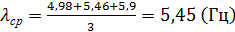(28)

Недостатком разностного метода является то, что этот метод неустойчивый и зависит от шага разностной аппроксимации по времени. Чем меньше шаг разностной аппроксимации, тем точнее результат математической модели (точнее представлена производная), а также критерием выбора является условие, когда разность значений двух решений не превышает 5%.

На основании выше написанного утверждения считаем, что для описания одного полного колебания достаточно 10 точек:

где Т – период одного колебания (обратно пропорционален частоте колебаний).

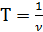(30)

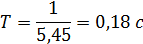
Рассчитываем шаг аппроксимации по уравнению (29):

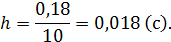
Принимаем шаг аппроксимации для удобства построения графиков зависимостей

Дата добавления: 2019-03-09; просмотров: 874; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 Следующая ⇒

Мы поможем в написании ваших работ!